推导欧勒动力学方程的一种新方法

林景波

(延边大学 理学院物理系，吉林 延吉 133002)

1 引言

欧勒动力学方程是描述刚体绕定点o转动的动力学方程，在确定刚体的运动情况过程中起重要作用[1].一般导出该方程采用的是矢量力学方法，通过作两次简化而完成[2，3]，即：(1)采用固着在刚体上的动坐标系，以使六个惯量系数Ixx、Iyy、Izz、Ixy、Iyz、Izx都是常数；(2)取用o点上的惯量主轴为动坐标系的坐标轴，以消去惯量积Ixy、Iyz和、Izx.而本文所提出的导出方法虽然在描写刚体动能时也取惯量主轴为动坐标轴，但是导出过程却完全区别于上述方法，采用的是分析力学方法，用哈密顿力学中的正则方程直接导出欧勒动力学方程，这种方法体现出哈密顿力学在解决力学体系问题时的优越性，从一个侧面表明在哈密顿力学中由于引入了正则变量，使其具有完备的理论价值和实践价值[4].

2 用正则方程导出欧勒动力学方程

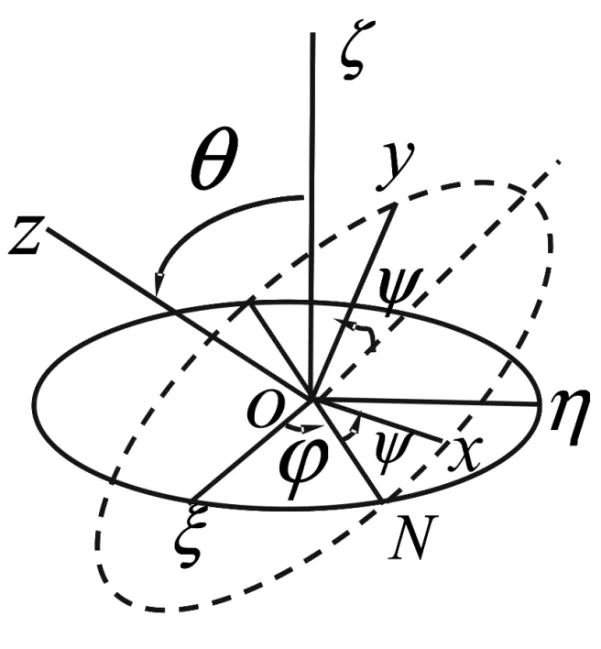
图1 欧勒角

如图1所示[5]，刚体绕定点o转动，o-ξηζ为固定坐标系，o-xyz为固着在刚体上，随刚体一起转动的动坐标系，当取o点上的惯量主轴为固着在刚体上的动坐标轴ox、oy、oz时，刚体动能可表示为：

若用图1中的欧勒角及相应的欧勒角速度表示刚体角速度在本体惯量主轴坐标轴上的分量，有：

因势能V一般不包含广义速度[6]，所以由L=T-V，得：

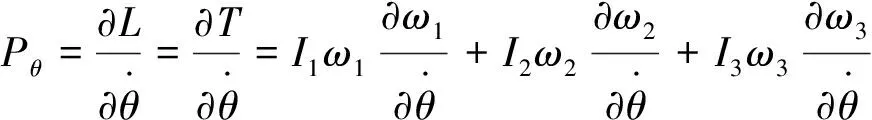
(1)

由(1)式解出:

(2)

按哈密顿函数定义：[7]

(3)

将(2)式代入(3)式中得哈密顿函数H表达式为:

正则方程可由(3)式求得：

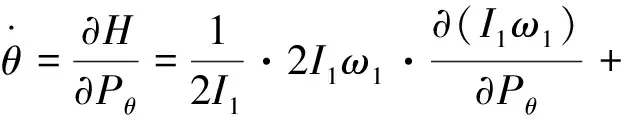
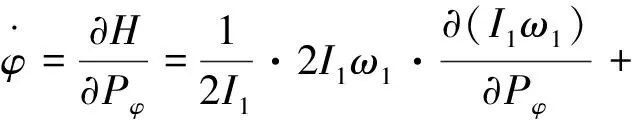
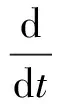
其中Qψ为对应于自转角Ψ的外力矩，即外力矩在O2轴的分量，可以表示为Qψ=M3，则有：

上式是欧勒动力学方程的第三式，其余的第一式和第二式，则不能直接由关于θ和φ的相应拉格朗日方程求得.因为如图1所示，由推出的正则方程知:θ和φ只有分别绕ON和Oζ轴转动时才改变，而不是在绕Ox和Oy轴转动时改变.而根据已求得的式子具有关于角速度的对称性，其余的第一式和第二式可以这样处理：使每个惯量主轴轮流处于Oz轴的地位，轮换主轴转动惯量和对应角速度分量的排列顺序，按照第三式可直接写出.于是欧勒动力学方程如下：

[1]周衍伯.理论力学[M].北京：高等教育出版社，1986：210.

[2]A.Ⅱ.马尔契夫.理论力学[M].北京：高等教育出版社，2006：139.

[3]GoldsteinH，PooleC，SafkoJ.ClassicalMechanics[M].3rded.AddisonWesley，2002:130.

[4]宫衍香，马秋红.哈密顿和哈密顿力学[J].现代物理知识，2006，18(5):65.

[5]孟志鹏，王志平.欧勒角的获得[J].延安大学学报学报，1998，19(3):47.

[6]鞠国兴.关于分析力学中势能的一个注记[J].大学物理，2007，26(12):20.

[7]薛纭，罗绍凯.分析力学基本问题及其变分原理的研究进展[J].上海应用技术学院学报，2008，25(4):45.