封闭爆炸近场地震纵波及横波质点速度模型*

李学政，张诚鎏，刘文学

（西北核技术研究所，陕西 西安 710024）

封闭爆炸近场地震纵波及横波质点速度模型*

李学政，张诚鎏，刘文学

（西北核技术研究所，陕西 西安 710024）

基于第四纪黄土层小爆炸当量系列封闭爆炸的近场地震观测数据，对纵波和横波分别进行了分析处理，获得了纵波和横波的质点速度，确定了纵波和横波质点速度现有模型的参数。综合分析了有代表性的3个模型，得出现存模型本质上的差别在于爆炸当量指数不同。对此提出了双极模型，并介绍了该模型参数的计算方法。对这几种模型在描述观测和实测数据方面的残差进行了比较。结果表明，双极模型反演数据与观测数据之间的残差平方和最小，而传统模型中最好的效果仅是接近双极模型。

爆炸力学；质点速度；封闭爆炸；近场地震；双极模型

工程爆破地震效应中有关的地运动参数普遍受到关注［1－2］，这些参数直接和岩土松动与破碎、矿山开采、坑道工程和地震探矿等众多领域密切相关。一些学者［2－5］对近地表爆炸地震的地面竖向振动速度地表效应和随机特性进行了研究，给出了地面竖向振动速度的理论模拟结果，在随机统计特性上与实验结果具有较好的一致性，而用短时傅立叶变换和基于小波变换理论的时频分析方法对地震效应的时间－频率特征的分析结果表明，小波变换方法可以更好地给出爆炸地震效应的细节信息。然而，在具体应用领域中，特别是在爆炸拆除、爆炸安全距离估计和地震探矿中，不仅关心爆炸地震幅值大小，而且关注爆炸地震引起的振动参数随观测距离和爆炸当量的变化。

已建立了众多地运动参数与爆炸当量及观测距离的关系，这些数据大多是通过矿山开采和人类工程采集的，所涉及的爆炸当量是数十吨甚至数百吨TNT，观测距离为几千米至数百千米，爆炸能量往往有相当大的部分消耗到空气中，而有关完全封闭爆炸，特别是几千克、数十千克直至数百千克的封闭爆炸地震资料相对缺乏。爆炸源所处的空间位置不同，爆炸能量在空气和介质中的能量分布差别较大，如果炸药中心位于地表水平面上，分别有65%和35%的能量传到空气和土中；如果炸药的下底位于地表水平面上，分别有78%和22%的能量传到空气和土中。而且爆炸地震传播对介质的依赖性很强，对于不同的介质条件，地震波传播规律也存在显著差异。由于考虑到地震破坏效应，传统上往往考虑的是最大速度模型，而爆炸最大速度往往不是同类波形，数据之间相关性较低。

本文中，基于黄土层爆炸当量千克级至百千克级一系列封闭爆炸的地震观测数据，分别对纵波和横波进行分析处理，计算爆炸地震纵波和横波质点速度随爆炸当量和观测距离的变化，确定质点速度模型。并提出双极模型，该模型能够同时实现相关系数为极大、实测与模型计算数据间残差平方和极小。详细介绍该模型参数的计算方法，并对这几种模型在描述观测数据方面的残差进行比较。

1 数学模型的建立

1.1 模型理论分析

物理上爆炸地震的质点振动参数与爆炸当量、爆炸方式、爆炸源的埋深、源区介质、传播路径、观测点地质条件等多种因素有关，这些因素作用的表现形式为爆炸地震波的激发、耦合或衰减等效应。爆炸当量为激发爆炸地震的能量源，显然，爆炸当量越大，激发出的应力波和地震波越强。爆炸方式、源区介质和爆炸源的埋深影响到能量耦合［6－8］，对于相同的爆炸当量，因爆炸源所在的介质不同，爆炸能量耦合到地层中的能量差别很大。一般，硬岩耦合系数高，软岩耦合系数低；封闭式耦合系数高，喷发式耦合系数低。由于介质的吸收和球面扩散作用，地震波参数随观测距离增大而发生非线性衰减。于是，质点振动参数p可表示为

式中：质点振动参数p包括位移、速度或加速度，W 为爆炸当量，R为观测距离；η为能量耦合系数，是变量c1、c2和c3的函数，c1、c2和c3分别表示爆炸方式、爆炸埋深和源区介质等因素。

1.2 现存模型

根据上面分析可知，爆炸地震参数除与爆炸当量、传播距离明显有关外，还和能量耦合系数有关，而爆炸方式、爆炸埋深和源区介质直接影响能量耦合系数。针对具体问题，研究者们提出众多数学模型或称经验公式时，对封闭爆炸与抛洒爆炸、硬岩与黄土等分别进行研究，从而简化了模型。但归结起来，具有代表性的模型有以下3种。

P.B.Attwell等［9］提出了地震动最大速度模型Ⅰ为

式中：K 为场地系数，K＝0.013～0.148，α＝0.64～0.96。

郝保田［10］根据高能封闭爆炸地震动观测数据，提出了最大速度模型Ⅱ为

式中：K＝8.2，α＝2.23。

谢毓寿等［11］基于大量的工业化爆数据，对经验关系进行了深入研究。根据炸药量为50g的实验数据，得出质点速度随观测距离的衰减因子为约－1.8，采用爆炸当量0.1～2.0kg的爆炸地震观测数据，观测距离在35～404m之间，爆炸当量指数为约0.6。提出地震动最大速度模型Ⅲ为

上式可改写为v＝KWαRβ，场地为坚硬基岩时，K1＝2.2～2.6，α＝0.60，β＝－1.8。

1.3 双极模型

式（2）～（4）有一个共同特点，质点速度都是爆炸当量与观测距离的函数，但又分为2类：（1）质点速度是以爆炸当量和观测距离为变量的函数，如式（4）；（2）质点速度是爆炸当量和观测距离的复合函数。其复合函数又有2种，详见式（2）和（3）。根据上述公式及参数的分布范围计算可知，爆炸当量指数在0.33～0.96之间。上述3个模型中，由于模型Ⅲ是一个二元函数，当爆炸当量范围较宽、实验次数较多时，统计处理结果相对可靠。模型Ⅰ和Ⅱ的复合变量形式上是不同的，但是，通过恒等变形，均可变为同一种形式。由此看出，模型比例距离的爆炸当量指数差别较大。换句话说，由于在比例距离计算中所选取的爆炸当量指数不同，才出现了不同的模型，在预测数据时，精度也不同。模型建立的目的就是使模型预测的数据和观测数据尽可能地接近，既然决定爆炸当量模型的本质是爆炸当量指数的选取，在此对上述模型Ⅰ和Ⅱ进行统一，选取最优的爆炸当量指数，使数据间相关系数最大，使模型反映的数据与观测数据之间的残差平方和最小，简称双极模型Ⅳ，可表示为v＝K（Wα／R）β 。

图1 爆炸源与测点分布示意图Fig.1Layout of explosion sources and observation points

2 观测数据

2.1 观测概况

所用的地震计有2种，3D-lite和 CMG-40T。3D-lite为三分向速度地震计，速度频响在1～80Hz范围内为一平直线，速度换能灵敏度为400V／（m／s），地震计噪声小于3nm／s；CMG-40T速度频响为0.033～50Hz，速度换能灵敏度为2kV／（m／s）。

在地层为第四纪黄土层地区10km2多的范围内，在爆炸源的东南－西北方向，距爆炸源0.60～2.50 km的范围内，布设了10多个地震测点，测点与爆炸源呈半包围形式，爆炸源和测点分布见图1。

爆炸源被埋放在地下20m处，上覆土层封闭，爆炸当量为千克级至百千克级。为了研究地震波质点速度随爆炸当量的变化，应保证爆炸源处的介质和位置“不变”，尽可能缩短爆炸源位置间的距离，所有爆炸源布设在半径约50m的较小区域内。

在野外黄土介质中进行了多次系列封闭小爆炸当量化爆，获得了一批地震数据，除个别测点因本底噪声较大或震中距较远，记录资料信噪比较小外，大多数观测记录波形完整、初至清晰。

2.2 观测结果

近场地震记录波形如图2所示，宏观上可以看出，所有的波形频率均在10～30Hz范围内，观测距离越长，波形的持续时间也越长，频率也越低。每条记录明显发育2个震相，前段为纵波，后段为横波。对记录进行了分析处理，获得了纵波质点速度和横波质点速度。在此列出了3次爆炸记录波形处理结果，如表1所示，R为观测点到爆炸源的距离，v为质点速度，下标“l”和“t”分别代表纵波和横波，“50、8、100”分别代表50、8、100kg的爆炸当量。

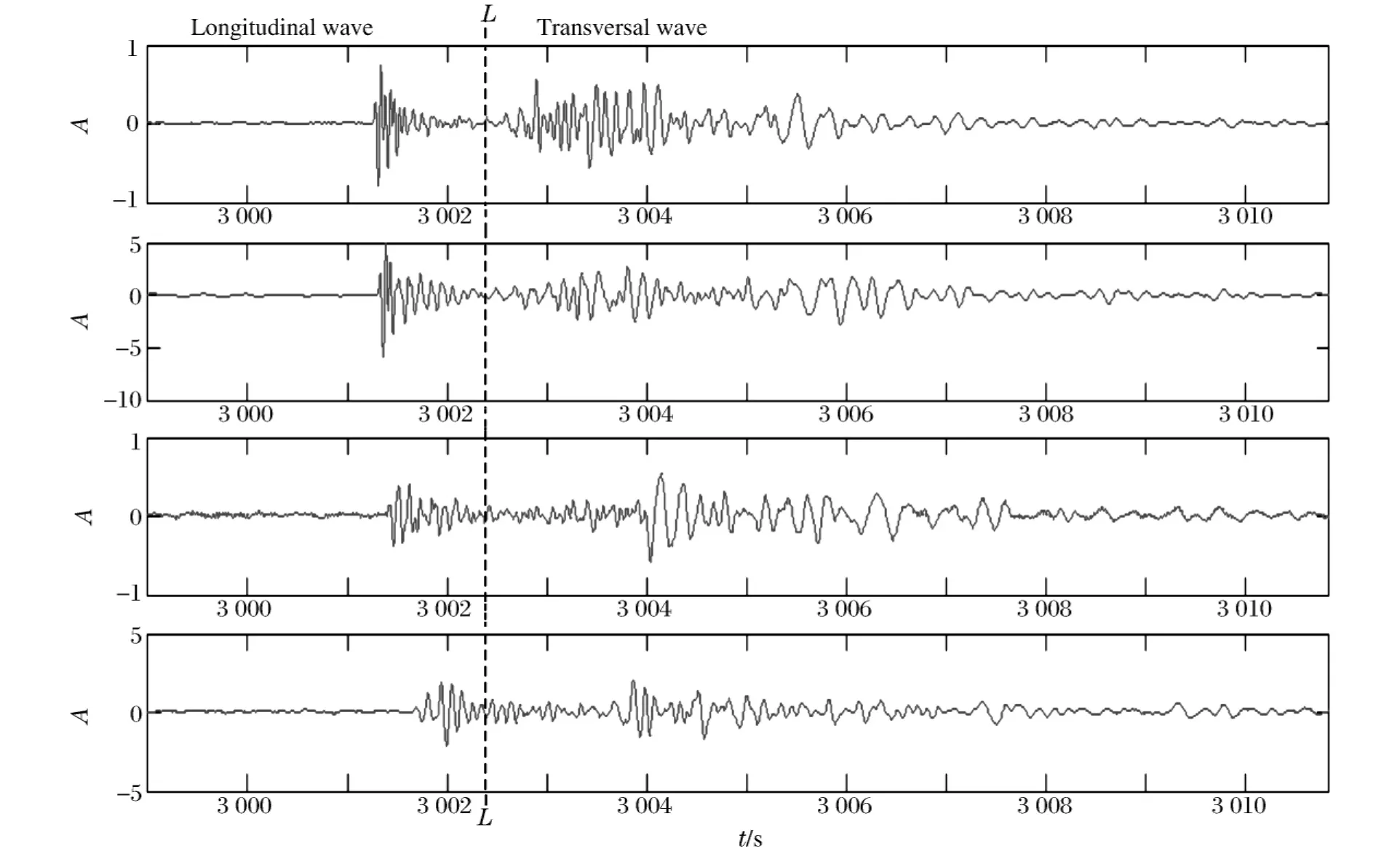
图2 爆炸地震垂直向波形Fig.2 Seismic waves from an explosion earthquake

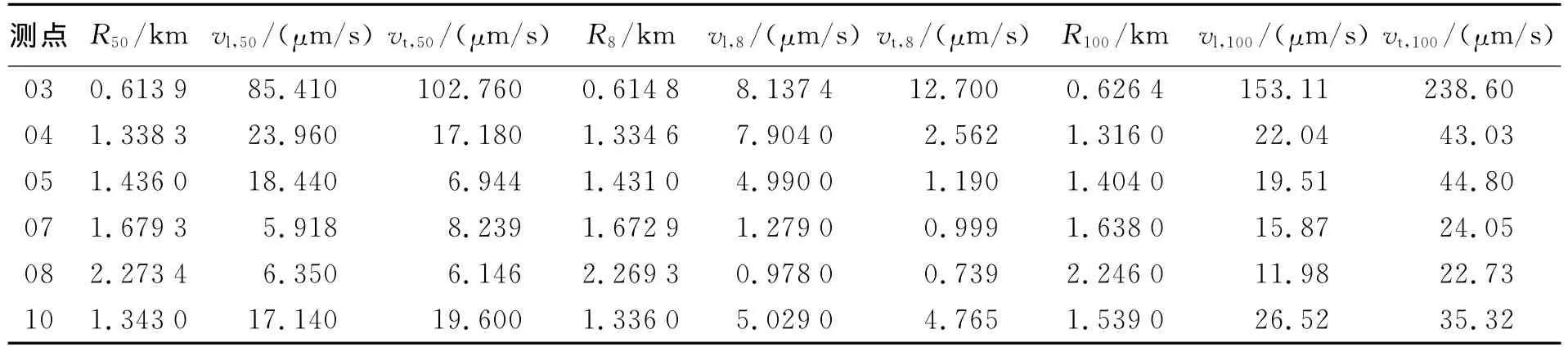
表1 黄土层中B2小爆炸当量封闭爆炸地震动垂向速度部分数据Table 1 Partial vertical velocities of low-yield explosion earthequake in soil for explosion B2

3 传统模型

3.1 资料预处理

场地地震观测点未变，只是爆炸源位置发生了少量变化，爆炸方式完全密封，场地的本底噪声为约0.5μm／s，总体上观测数据质量是好的。宏观上，测点质点速度随爆心距的增大而变小。但是，由于自然介质的复杂性、爆炸源工程上实现的技术差异，地震波传播过程中，数据还是具有一定的分散性。由于测点局部地质条件所致，如2号爆炸，观测点3和观测点4，距离相差近一倍，而纵波质点速度相差并不显著，而个别测点的质点速度出现异常，在模型建立时，将被视为奇点而剔除。

3.2 模型的建立

3.2.1 显函数模型

模型Ⅲ为爆心距和爆炸当量的显函数模型，需要确定距离衰指数β和爆炸当量指数α。只要所有观测点在一条直线上，或在各向同性的介质中，通过观测一次或多次爆炸在不同距离上的地震数据，即可计算β。固定爆炸源位置，通过改变爆炸当量，根据观测资料，即可确定爆炸当量指数α。由于爆炸冲击效应，爆炸源处介质结构受到破坏，工程技术上很难实现爆炸源的位置完全重复，因此，爆炸当量指数α不易准确确定。而表1中的各次爆炸源相对位置变化不大，仅为数10m，震中距离变化也不大，均在1%～2%之间，因此，可认为爆炸源位置不变。

回归结果如图3、表2和表3所示，纵波质点速度vl的距离衰减指数βl介于－2.13～－1.67之间，均值为约－2.0，相关系数γl在－0.97～－0.78之间；而横波质点速度vt的距离衰减指数βt介于－2.30～－1.97之间，均值为约－2.2，相关系数γt在－0.97～－0.92之间。比较发现，横波质点速度与观测距离的相关性更显著。

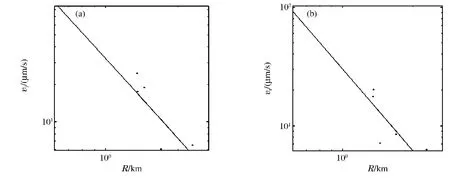
图3 B2爆炸质点速度与观测距离的关系曲线Fig.3 Relation between particle velocities and observation distances for explosion B2

表2 距离衰减指数Table 2 Distance attenuation exponents

纵波和横波质点速度随爆炸当量的变化也不相同，纵波质点速度随爆炸当量变化的指数αl在0.45～1.17之间，横波波质点速度随爆炸当量变化的指数αt在0.78～1.34之间。上述数据表明，质点速度随爆炸当量变化的指数存在一定的分散性，横波质点速度随爆炸当量增加而增大较快。

根据3次爆炸地震观测，计算了模型Ⅲ的参数，纵波Kl分别为1.17、1.32和1.23，均值Kl为约1.24，横波Kt分别为0.44、0.36和0.42，均值为约0.41。计算数据表明，尽管爆炸当量差别较大，K值仍具有较好的一致性。

于是模型Ⅲ的纵波和横波质点速度分别为

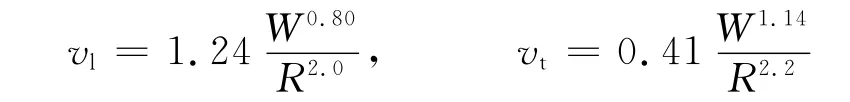
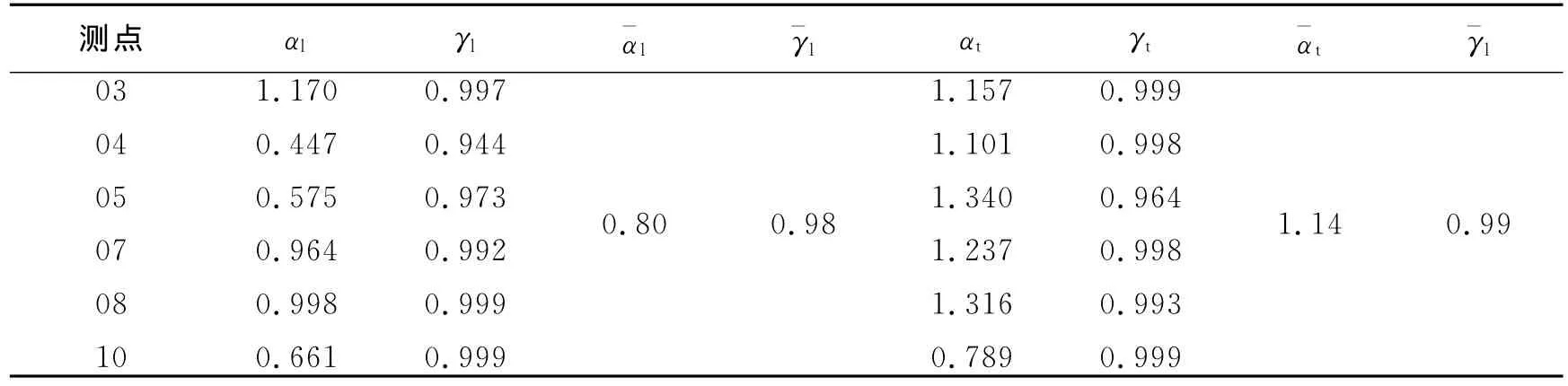
表3 爆炸当量指数Table 3 Yield exponents

3.2.2 复合函数模型

复合函数模型以模型Ⅰ和模型Ⅱ为代表，都是将爆炸当量和观测距离的比例作为一个变量，模型的差别表现在计算爆炸当量和观测距离比例时，采用了不同的爆炸当量指数。首先计算各个模型比例距离，然后再进行数据拟和，模型中，比例距离的指数α和参数K的计算结果如表4和图4所示，其中b为截距，σ为方差，下表“l”和“t”分别代表纵波和横波。

表4 复合函数模型计算结果Table 4 Calculated results of compound function models

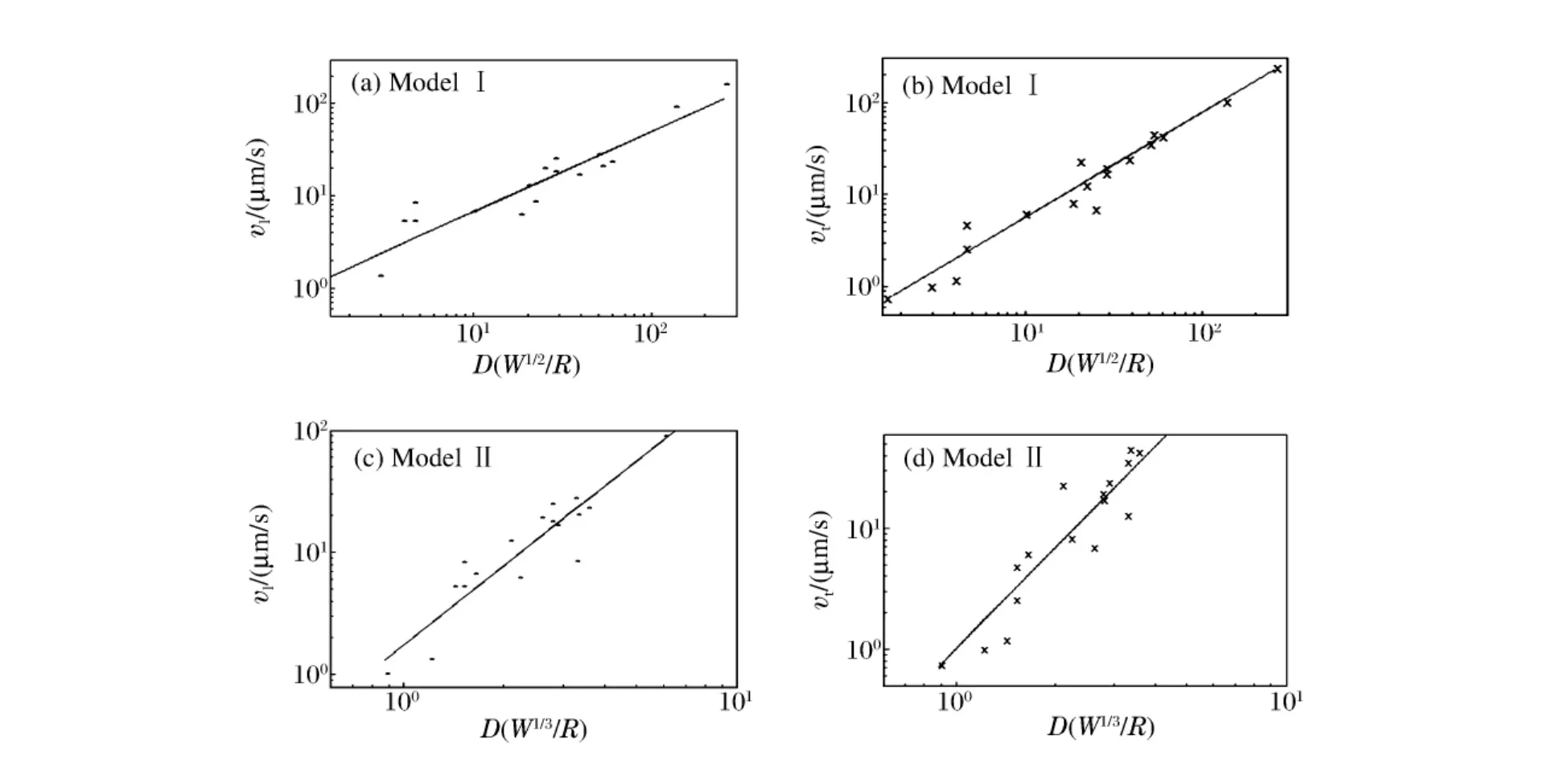
图4 模型Ⅰ和模型Ⅱ纵波和横波质点速度的拟合曲线Fig.4 Fitted particle velocity curves of longitudinal and transversal waves based on modelsⅠandⅡ

4 双极模型

双极模型，称为模型Ⅳ，有2个参数，分别是爆炸当量指数和比例距离指数，通过2个步骤，可以计算数值的大小。首先设定爆炸当量指数，对所有观测数据进行预处理，然后进行回归，计算出比例距离指数β、截距b、相关系数γ和质点速度残差平方和σ，然后改变爆炸当量指数，再计算残差和等。这样反复循环计算，当残差和最小时所对应的参数α和值β，即为所求的模型参数。

本模型具体计算时，设定指数α在1／1.0～1／3.0范围内按照一定间隔变化，并计算比例距离，然后进行回归。不同爆炸当量指数所对应模型的相关系数和数据残差不同。相关系数是一条凹向下的具有极大值的曲线，残差是一条凹向上的具有极小值的曲线，如图5所示。图5（c）和（d）分别为纵波相关系数γl和残差σl曲线，爆炸当量指数为1／2.4时，相关系数最大，残差最小。图5（e）和（f）分别为横波相关系数γt和残差σt曲线，最小残差对应的指数为1／2.0。图5（a）和（b）分别第四纪黄土层纵波和横波模型Ⅳ拟和曲线，详细计算结果如表5所示，模型Ⅳ的纵波和横波质点速度分别为

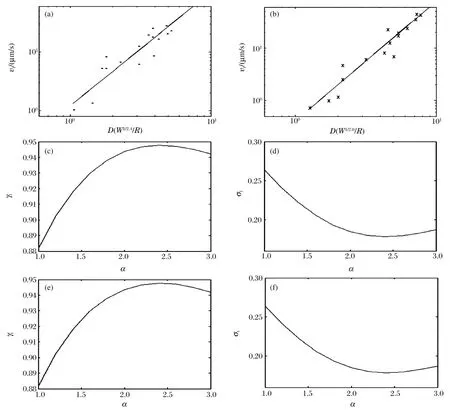
图5 关于模型Ⅳ的质点速度、残差和相关系数Fig.5 Particle velocities，remains and related coefficients on modelⅣ

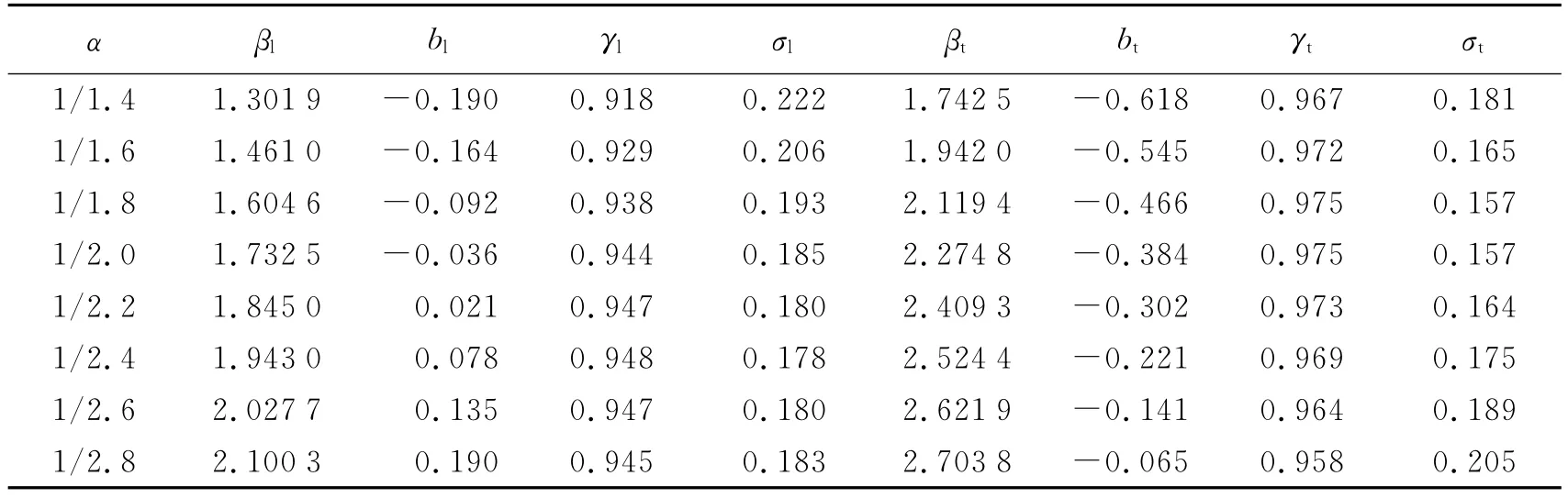
表5 模型Ⅳ不同α计算结果部分数据Table 5Partial calculation data on modelⅣin the case of different yield exponents

5 模型比较

在显含模型数据处理中，爆炸当量指数是通过固定爆炸当量的位置不变得到的，这一假定，在物理上较难实现。其一，由于爆炸当量不同，爆炸的埋深不同；其二，尽管在各次爆炸中，爆炸源位置间距很短，但位置不可能作到完全重复。该模型的参数与模型Ⅱ的参数接近。

表4中给出了模型Ⅰ和模型Ⅱ的计算参量，纵波的比例距离指数分别为0.866和2.162，而相关系数分别为0.943和0.942，方差分别为0.185和0.198。数据表明，这2个模型在描述观测数据的变化规律方面存在一定的差异，模型Ⅰ描述各观测数据效果较好。2个模型的横波相关系数分别为0.975和0.951，方差分别为0.156和0.220，显然，模型Ⅰ能较好地描述近场地震波的传播规律。对于同一种模型而言，纵波和横波相比，未表现出哪种震相的模型在反映质点速度变化规律方面具有更强的优势。

由表5可知，模型Ⅳ中纵波爆炸当量指数为1／2.4时，相关系数最大为0.948，残差最小为0.178。与模型Ⅰ相比，该模型能够更好地描述地震波质点速度的变化规律。模型Ⅳ中当横波爆炸当量指数为1／2.0时，残差最小为0.157，而与模型Ⅰ相比，二者残差基本一致。换句话说，无论是纵波还是横波，在模型计算数据与观测数据一致性方面，模型Ⅳ是最佳的，二者之间的残差平方和最小，而传统的有代表性的3个模型中最好的结果仅是接近双极模型。

6 结 论

物理上爆炸地震的质点振动参数与爆炸当量、爆炸方式、源区介质、传播路径、观测点地质条件等多种因素有关，这些因素作用的表现形式为弹性波激发、耦合和衰减。因此，质点振动速度可表示为爆炸当量、观测距离和能量耦合的函数。

纵波和横波质点速度随爆炸当量呈指数变化，纵波当量指数为0.80，横波当量指数为1.14；纵波和横波质点速度随距离衰减指数不同，纵波衰减指数为2.0，横波衰减指数为2.2。数据表明，横波与纵波相比，质点速度随爆炸当量增大而增大较快，随距离增大而快速衰减。

综合分析了有代表性的3个模型，得出模型本质上的差别在于爆炸当量指数不同。对此提出一种双极模型，介绍了该模型参数的计算方法，并对这几种模型在描述观测和实测数据方面的残差进行了对比。无论是纵波还是横波，双极模型反演数据与观测数据之间的残差平方和最小，而传统模型中最好的结果仅是接近双极模型。

［1］刘爱文，俞言祥，付长华，等.50t科学爆破振动的衰减特征及地形效应［J］.爆炸与冲击，2010，30（1）：21-26.

LIU Ai-hua，YU Yan-xiang，FU Chang-hua，et al.Attenuation characteristics and topographic effect of a scientific explosion with 50texplosive［J］.Explosion and Shock Waves，2010，30（1）：21-26.

［2］刘晶波.局部不规则地形对地震地面运动的影响［J］.地震学报，1996，18（2）：239-245.

［3］林大超，张奇，白春华.爆炸地震效应的时频分析［J］.爆炸与冲击，2003，23（1）：32-36.

LIN Da-chao，ZHANG Qi，BAI Chun-hua.Time-frequency analysis of explosion seismic effects［J］.Explosion and Shock Waves，2003，23（1）：32-36.

［4］张雪亮，黄树棠.爆破地震效应［M］.北京：地震出版社，1981：159-161.

［5］Iyama J，Kuwamura H.Application of wavelets to analysis and simulation of earthquake motions［J］.Earthquake Engineering ＆ Structural Dynamics，1999，28（3）：255-272.

［6］李孝兰.空腔解耦爆炸实验研究的基础理论［J］.爆炸与冲击，2000，20（2）：186-192.

LI Xiao-lan.Basic theory of decoupled explosions in cavities［J］.Explosion and Shock Waves，2000，20（2）：186-192.

［7］Haskell N A.A static theory of the seismic coupling of a contained underground explosion［J］.Journal of Geophysical Research，1961，66（9）：2937-2944.

［8］Glenn L A.Energy-density effects on seismic decoupling［J］.Journal of Geophysical Research，1993，98（2B）：1933-1942.

［9］Attewell P B，Farmeer I W，Haslam D.Prediction of ground vibration parmeters from major quarry blasts［J］.Mining and Materials Engineering，1965：621-626.

［10］郝保田.地下核爆炸及其应用［M］.北京：国防工业出版社，2002：227-229.

［11］谢毓寿，王耀文.工业爆破的地震效应［J］.地球物理学报，1962，11（2）：154-161.

HSIEH Yü-show，WANG Yao-wen.Seismic effect of construction blasting［J］.Diqiu Wuli Xuebao，1962，11（2）：154-163.

Particle velocity models of longitudinal and transversal waves in the near field of sealed explosions＊

LI Xue-zheng，ZHANG Cheng-liu，LIU Wen-xue
（Northwest Institute of Nuclear Technology，Xi’an 710024，Shaanxi，China）

The seismic data of low-yield explosion earthquakes which took place in the Quaternary period soil were based on to calculate the particle velocities of the longitudinal and transversal waves and determine the parameters for the existent models.The three representative models were synthetically analyzed.It displays that the difference of the existent models lies in different yield exponents.Accordingly，a double-extreme model was proposed and the calculation method of the model parameters was introduced in detail.Comparison of these models shows that the data calculated by the double-extreme model is the most consistent with the real observation and the amplitude error between them is the smallest.The best results calculated by the traditional velocity models only approach these calculated by the double-extreme model.

mechanics of explosion；particle velocity；sealed explosion；near-field earthquake；double-extreme model

4February 2010；Revised 22July 2010

LI Xue-zheng，lixuezheng01＠yahoo.com.cn

（责任编辑 张凌云）

O384 国标学科代码：130·3599

A

1001-1455（2011）02-0196-08＊

2010-02-04；

2010-07-22

李学政（1957— ），男，博士，高级工程师。