导管架式海洋平台自适应预测逆控制研究

崔洪宇，洪 明，周 平，赵德有

（大连理工大学 船舶工程学院，辽宁 大连 116085）

导管架式海洋平台自适应预测逆控制研究

崔洪宇，洪 明，周 平，赵德有

（大连理工大学 船舶工程学院，辽宁 大连 116085）

文章提出了一种新的基于动态刚度阵法的导管架式海洋平台模糊神经网络自适应预测逆控制模型。该模型是通过安放在海洋平台桩腿上的压力传感器实时采集海洋平台所受波浪力，然后应用动态刚度阵法快速而准确地计算出平台顶部的响应，再将此响应作为模糊神经网络预测逆控制器的输入信号，预测出下一时刻平台顶部的控制力来对海洋平台振动响应进行控制；同时，通过反馈的自适应预测逆控制器来减小扰动和前馈控制的误差。为了验证该模型的抗干扰能力，文中还对有随机风载荷扰动情况下的导管架式海洋平台主动控制进行了研究。最后的数值算例结果表明，文中所提出的导管架式海洋平台主动控制模型具有较强的抗干扰能力，能很好地解决控制系统中存在的时滞问题，可有效地控制导管架式海洋平台的振动响应。

导管架式海洋平台；动态刚度阵；预测逆控制；模糊神经网络；波浪载荷；风载荷

fuzzy neural network;wave force;wind force

1 引 言

近年来，随着海洋开发的不断发展，越来越多的大型柔性海洋平台被用于海底钻探和石油开采之中。这些海洋平台长期工作在恶劣的海洋环境中，经常要承受风、浪、流、地震和潮汐等环境载荷的作用。在这些环境载荷的作用下，海洋平台极有可能发生有害振动。振动响应过大不但会危害人员的身心健康、使平台设备仪器损坏，而且会引起结构疲劳破坏、降低平台可靠性，威胁结构安全。因此如何有效地控制平台的振动响应就显得非常重要。

在过去的几十年里国内外许多专家学者已经对海洋平台结构振动控制进行了广泛的研究，并且取得了丰硕的成果[1]。研究表明被动控制虽然有着自身的一些优点，但只能采用改变海洋平台固有频率方法（如改变刚度、质量和阻尼）进行振动控制，由于波浪频带较宽，并且是随机的，被动控制难于实现。主动控制可以在全频域范围内有效地的抑制平台的振动，但经典和现代控制是基于精确数学模型的控制，对于海洋平台这种具有结构复杂、外载荷不确定的系统，以及控制过程中存在信号传输延时等原因，使得经典和现代控制都很难达到理想的控制要求。近些年发展起来的模糊、神经网络控制等智能控制方法是一种不基于被控对象模型的控制方法，它克服了经典和现代控制的缺点，具有强的稳定性、鲁棒性和处理非线性的能力，然而这些智能控制方法脱离了被控对象模型特征，使得被控系统实际的模型特征得不到应用。

本文在现有模糊神经网络和自适应逆控制方法基础之上，提出一种新的导管架式海洋平台主动控制模型，即基于动态刚度阵法的模糊神经网络自适应预测逆控制（DSM based on FNN APIC）模型，很好地解决了上述主、被动控制中存在的问题。该控制模型将动态刚度阵法快速而精确的建模特性、模糊神经网络强的处理非线性能力和自适应逆控制方法的优越控制性能融为一体，它既克服了经典和现代控制算法过度依赖于精确数学模型的缺点，又弥补了智能控制算法脱离被控对象模型的不足，而且很好地解决了控制过程中存在的时滞问题，具有较强的抗干扰能力，可以有效地控制导管架式海洋平台的振动响应。

2 基于动态刚度阵法的被控导管架式海洋平台模型建立

2.1 动态刚度阵法基本理论

动态刚度阵法的概念最早由Kolousek[2]于20世纪40年代早期提出，它是解决工程中结构振动问题的一个强有力的工具。动态刚度阵法与传统有限元方法或其它近似方法不同之处在于，它的刚度阵是由单元运动微分方程的解析解推导而来的，是频率的超越函数，并同时具有质量和刚度属性，可以准确地表示单元的属性。因此，动态刚度阵法可以按照结构的自然节点来划分单元，通过较少的自由度数来准确地计算结构固有频率和振动响应。本文利用平面Timoshenko梁单元动态刚度阵来建立被控导管架式海洋平台的计算模型，并将其用于对导管架式海洋平台的主动控制中。

平面Timoshenko梁单元动态刚度阵是从考虑剪切变形和转动惯量影响的Timoshenko梁理论建立的运动微分方程推导而得的[3]。

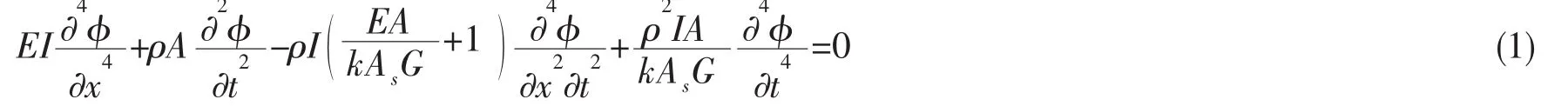
式中：φ表示横向挠度w或横截面的转角ψ；E、G和ρ分别是杨氏模量、剪切模量和材料密度；A、As和I为横截面面积、剪切面积和惯性矩；k是剪切修正系数。

梁单元自由弯曲振动时，假定 φ 随时间t正弦变化，即 φ（ x,t）=Φ（x） sinωt，Φ（x）=W（x）或 Ψ（x），W（x）和Ψ（x）分别是正弦变化的位移和弯曲斜率的幅值。

令ξ=x/L，其中L为梁单元的长度，则方程（1）可改写为：

根据动态刚度阵法推导的一般过程，由单元两端的广义位移和广义力的关系可得平面Timoshenko梁单元的动态刚度阵形式如下：

通过上式可计算出相应的平面Timoshenko梁单元的质量阵。所得的单元动态刚度阵和质量阵可按传统有限元方法进行组装[5]。

2.2 基于动态刚度阵法的导管架式海洋平台结构模型

导管架式海洋平台属于大柔度复杂结构，要准确计算其振动特性，通常都需要用有限元方法对平台进行详细的建模，这样的计算模型自由度非常多，对于结构振动主动控制来说，控制器的成本和计算时间随着被控系统自由度数的增加而成指数倍增长，使得此方法很难用于结构的振动主动控制中；如果要把平台简化成具有几个自由度的集中质量的模型时，在模型简化过程中，对刚度和集中质量的处理存在许多不确定因素，使得集中质量模型很难准确描述平台的动力特性；而动态刚度阵法可按结构自然节点来划分单元，减少了自由度数，简化了计算模型，提高了计算速度，而且计算结果也十分准确。平面桁架结构作为土木工程中一种较为常用的简化计算模型，它要比集中质量模型更能准确地反应平台的动力特性。考虑到对导管架式海洋平台的主动控制往往是针对其中某一个方向来实施，又由于大部分导管架式海洋平台结构是对称的，因此完全可将其简化成平面桁架结构。平台上的机械设备和舱室等质量平摊在平台相应位置的桁架上。边界条件是在平台底部6倍桩径处刚固。简化后模型使用Wittrick-Williams算法[6]来求解固有频率和相应的固有振型，平台的振动响应采用模态叠加法来计算。对具有n个自由度的受控导管架式海洋平台的振动运动方程为：

式中M、C和K分别为n×n阶的质量、阻尼和刚度矩阵，它们都是与频率相关的函数；y（t ）、（t ）和（t）是n维位移、速度和加速度向量；u（t）为m维控制力向量；f（t）为r维外扰力向量，n×m阶矩阵L和n×r阶L2分别是控制力和外扰力的位置矩阵。然后由杜哈梅尔积分直接求解（8）式来得到受控导管架式海洋平台每个振型下的响应，再将它们叠加起来，就得到整个平台系统受控后的响应。

3 基于动态刚度阵法的导管架式海洋平台模糊神经网络自适应预测逆控制系统

3.1 控制系统结构图

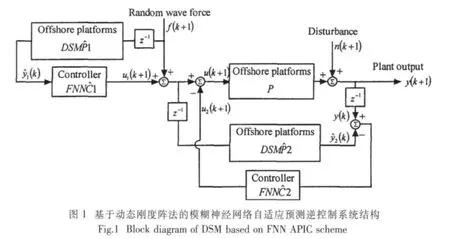
本文提出的基于动态刚度阵法的模糊神经网络自适应预测逆控制模型，结构如图1所示。首先通过安放在导管架式海洋平台桩腿处的压力传感器实时采集t时刻导管架式海洋平台所受随机波浪力f（k），然后由动态刚度阵法快速准确地计算出导管架式海洋平台系统DSM1在随机波浪力f（k）作用下平台顶部的响应），再将平台顶部响应（k）作为模糊神经网络自适应预测逆控制器FNN的输入信号，为了减小控制过程中存在的时延问题对被控平台系统控制性能的影响，由FNN预测出t+Δt时刻施加到平台顶部的控制力u1（k+ 1 ）来对导管架式海洋平台进行预测控制。由于自适应逆控制是一种前馈控制方法，被控导管架式海洋平台系统P的输出响应y与控制力u1输入之间没有反馈，使得平台系统P所受到的扰动n得不到控制。为了消除扰动n对平台系统P动态性能的影响，在t时刻将被控导管架式海洋平台系统P和动态刚度阵法建立的导管架式海洋平台模型DSM在波浪力f（k）和控制力u（k）联合作用下的响应之差作为预测逆控制器FNN的输入信号，将预测逆控制器FNN

1输出信号u2（k+ 1 ）在被控导管架式海洋平台系统P的控制端减去，由于预测逆控制器FNN为平台系统P的预测逆模型，这样扰动信号通过一个预测逆模型FNNC和一个正模型P以此来达到扰动消除的目的。由于控制器FNN为预测逆控制器，即通过t时刻的扰动信号n（k）来预测出t+Δt时刻的扰动信号n（ k+1 ），以此来减小控制过程中存在时滞对平台系统控制性能的影响。自适应逆控制对平台的动态性能的控制是通过预测逆控制器FNN进行的，而对扰动的消除是通过预测逆控制器FNN来进行控制，这不同于传统的反馈控制中将被控对象的动态性能和扰动一起处理，这样可以根据不同的条件尽量提高两个控制器各自的控制性能。

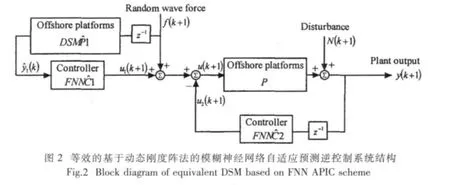
由于对导管架式海洋平台控制的理想情况是，控制后的平台P响应为零，所以在基于动态刚度阵法的导管架式海洋平台自适应预测逆控制系统中，可将动态刚度阵法建模及模糊神经网络预测、辨识的误差当作被控平台系统的扰动来处理，扰动信号为N（k），那么控制系统结构图1可以等效为图2所示结构。如此一来，可以直接通过传感器采集到的平台系统顶部的位移、速度和加速度响应作为自适应预测逆控制器FNN的输入信号。在图2中，由于控制器FNN和FNN都为平台系统P的预测逆模型，扰动信号N（k）通过一个逆模型FNN和一个正模型P，以此来达到扰动消除的目的。

3.2 模糊神经网络自适应预测逆控制器设计

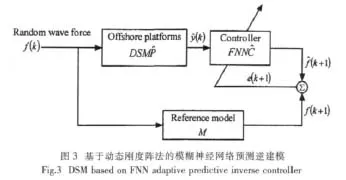
自适应逆控制是首先辨识出被控对象的逆模型，然后将此逆模型串联到被控对象的输入端作为控制器来控制被控对象的动态性能[7-8]。由于模糊神经网络具有很强的预测、辨识和处理非线性的能力，所以本文应用模糊神经网络来辨识被控导管架式海洋平台系统的逆模型，又因为在控制过程中存在信号传输延时等原因，使得控制系统的控制效果不是很理想，或者达不到控制要求，所以应用模糊神经网络来根据t时刻的平台顶部位移、速度、加速度响应预测出t+Δt施加于平台顶部的控制力。模糊神经网络辨识预测逆控制器的结构如图3所示。其中

式中M为导管架式海洋平台系统预测逆建模的参考模型。

3.3 模糊神经网络结构及训练算法

本文采用模糊神经网络是三个输入（平台顶部的位移、速度和加速度）单输出（预测的控制力）的六层前向网络[9]，网络结构如图4所示。设Oij为模糊神经网络第j层的第i个节点的输出。

第一层：为输入层，将输入数据传输到下一层：

其中xi为模糊神经网络第一层的第i个输入。

第二层：为模糊化层，将输入变量模糊化，输出对应模糊集的隶属度，在本文中模糊集的语言变量为7个，第i个节点对应的输出可以表示为：

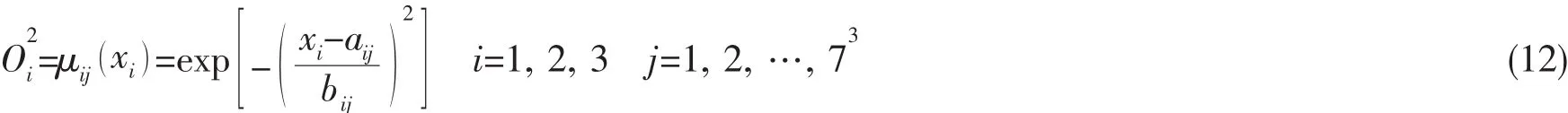
式中：j对应第三层的节点，μij为隶属度函数，其中aij为隶属度函数的中心，bij为隶属度函数的宽度。

第三层：为模糊规则推理层，实现模糊集的运算，第j个节点对应的输出可以表示为：

式中ωj为第j条模糊规则。

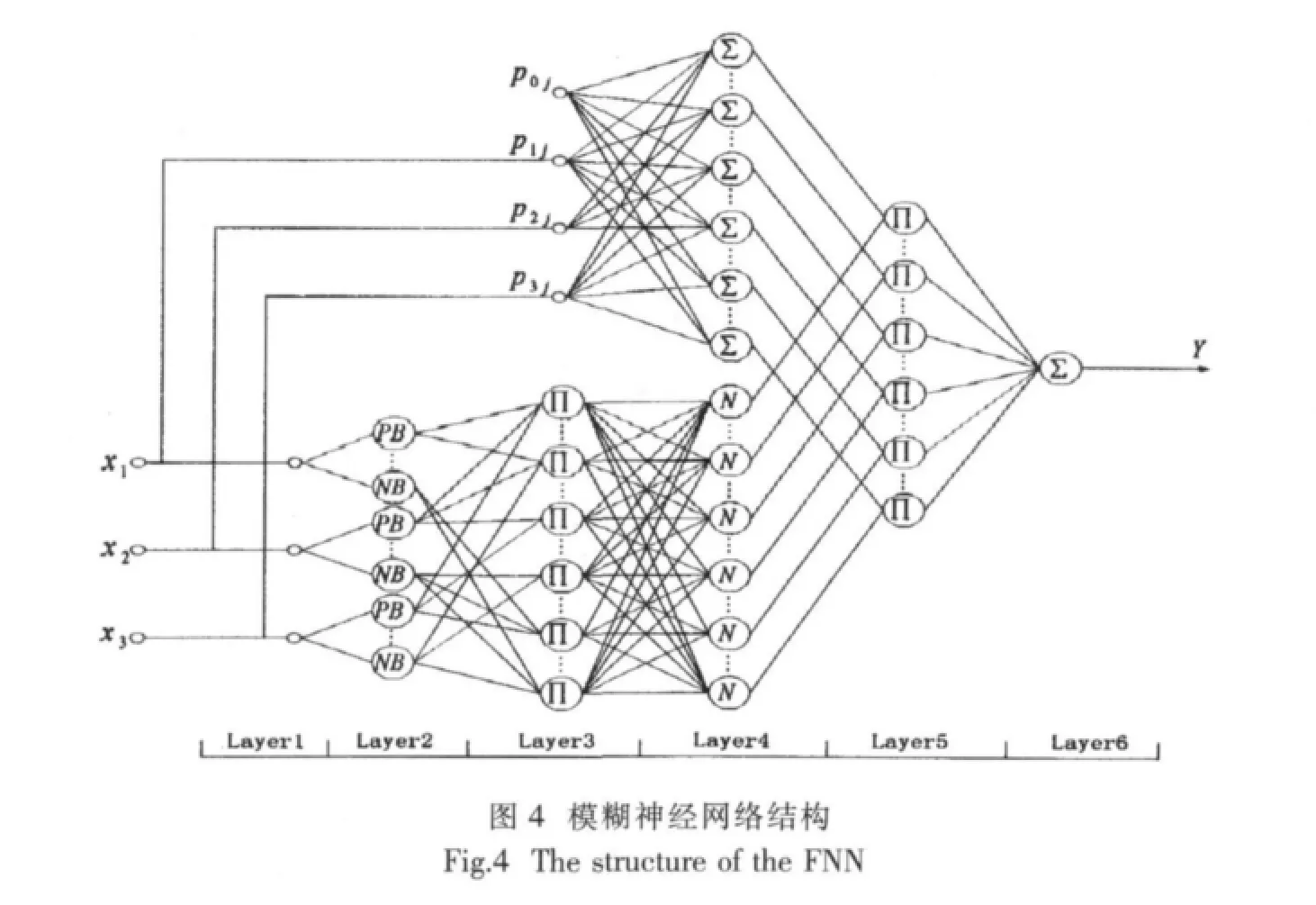
第四层：为各条模糊规则的适应度归一化层，第j个节点对应的输出可以表示为：

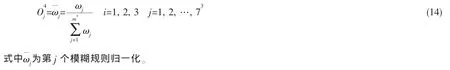
第五层：为去模糊化层，每个节点的传递函数为线性函数，表示局部的线性模型，第j个节点对应的输出可以表示为：

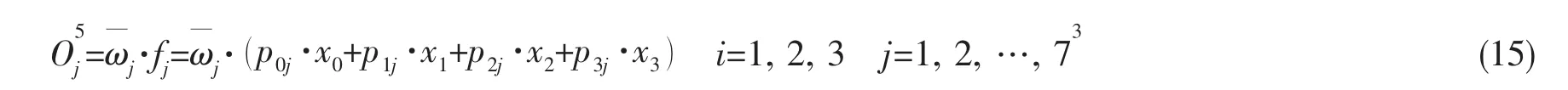
式中：x0=1，pij为线性函数 fj的系数。

第六层：为输出层，输出层节点为一个固定节点，计算所有输入信号的总输出：

式中Y为模糊神经网络的输出。

模糊神经网络的训练采用梯度下降的误差反向传播算法来调整参数，调整的参数包括隶属度函数的中心aij和宽度bij及线性函数的系数pij。训练前线性函数的系数pij的初始值取为-1～1之间的随机数，由于隶属度函数的中心aij和宽度bij的初始化决定输入空间的划分和模糊规则的数目，所以输入空间的划分采用常用的平均分割法来确定。

4 数值算例

4.1 导管架式海洋平台计算模型

本文对一综合性导管架式海洋平台在随机波浪力作用下的振动响应进行主动控制，模型如图5所示。平台结构总高140m（距离海床），设计水深80m，甲板的2层设备层和3层生活区组块高共计20m，甲板尺寸为 60×60m，导管尺寸（水平及斜杆）为 Φ0.8×0.02m，导管尺寸（竖杆）为 Φ1.6×0.04m，水平支撑4层。桩腿断面尺寸为Φ1.46×0.04，桩腿入土深为100m。导管架桩腿之间的间距比较大，远大于5倍至10倍桩腿直径，故相邻桩腿之间的群桩效应忽略不计。平台的等效质量分布对于平台动力特性有较大的影响，等效后由下至上各层的质量分布分别为：3000t、2500t、2000t、12000t。采用动态刚度阵法将导管架式海洋平台模型简化为图6所示的平面桁架结构。

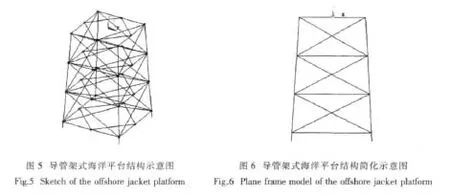
为验证简化模型，在表1中列出了简化后的平面动态刚度阵模型与三维有限元模型以及同样简化的平面有限元模型的前两阶固有频率的比较。从表中可以看出三者之间的固有频率十分接近，因此为了便于控制算法对某个方向的振动响应进行控制，根据平台的对称特性，完全可以将其简化为平面桁架结构来计算相应方向的动力响应。

表1 不同导管架式海洋平台计算模型的固有频率比较Tab.1 Natural frequencies of different offshore jacket platform models

4.2 随机波浪力作用下的导管架式海洋平台振动响应

作用在平台上的随机波浪力采用改进的P-M谱，并通过Morison公式计算得到[10]，如图7所示，其中随机波浪的有效波高Hs为8m，平均周期T0为8s；图8为模拟的作用在平台上的150s随机波浪力。

将图8所示的随机波浪力作用于上述导管架式海洋平台的计算模型上，通过模态叠加方法并直接积分可得到平台的时程位移响应幅值曲线，如图9所示。为了进一步验证动态刚度阵方法，对相同的简化平面导管架式海洋平台模型采用有限元方法来计算，计算结果同样在图9中列出。从图中可以看出，DSM和FEM方法的计算结果较为吻合，验证了本文的方法及计算程序的可靠性。

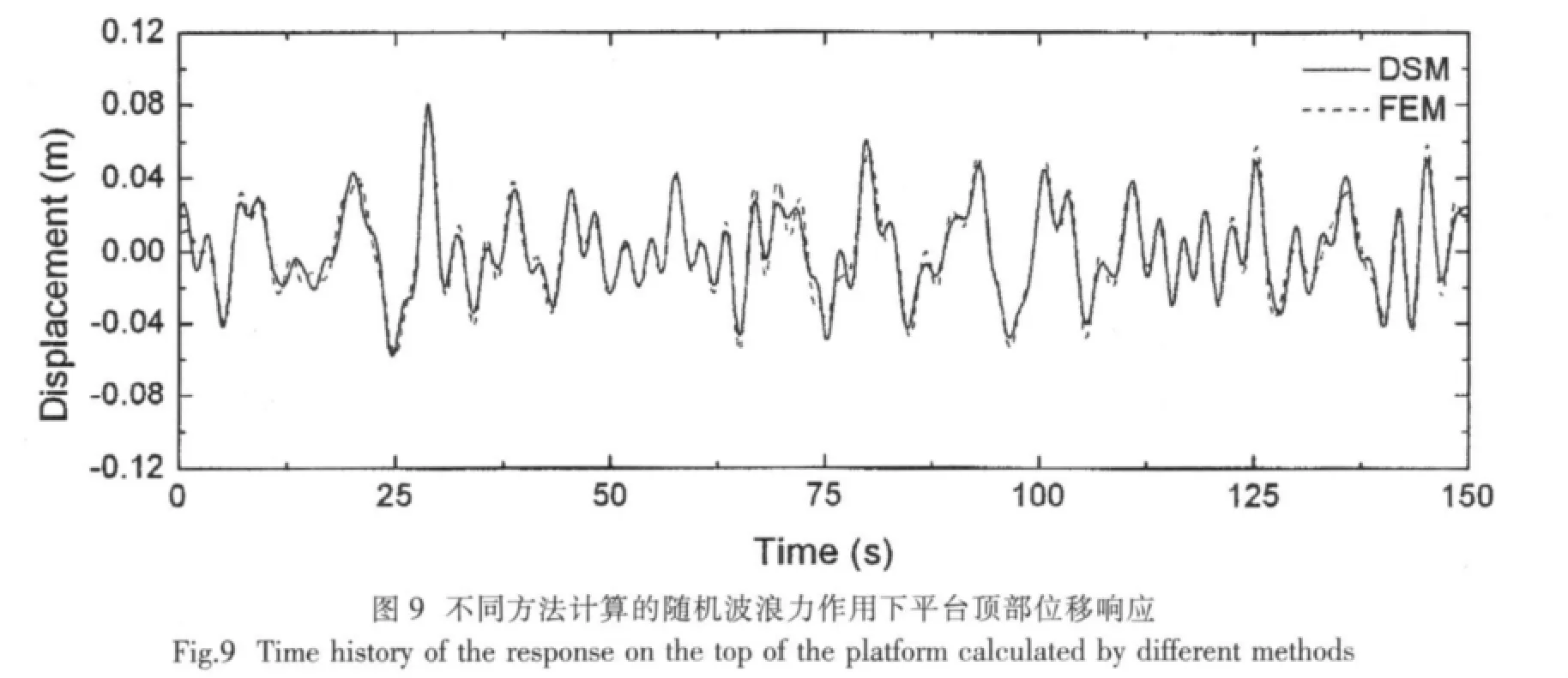
尽管上述两种方法的计算结果十分相近，但是它们所使用的计算时间却有非常大的差别，表2中给出了这两种方法对相同模型的计算时间比较，可以看出传统有限元方法在同等条件下，计算时程响应要比动态刚度阵法要多花费更多的时间。这也就是动态刚度阵的优点所在，也正因为其快速准确的特点，才使该方法有可能用于导管架式海洋平台的实时主动控制之中。

4.3 模糊神经网络训练及预测

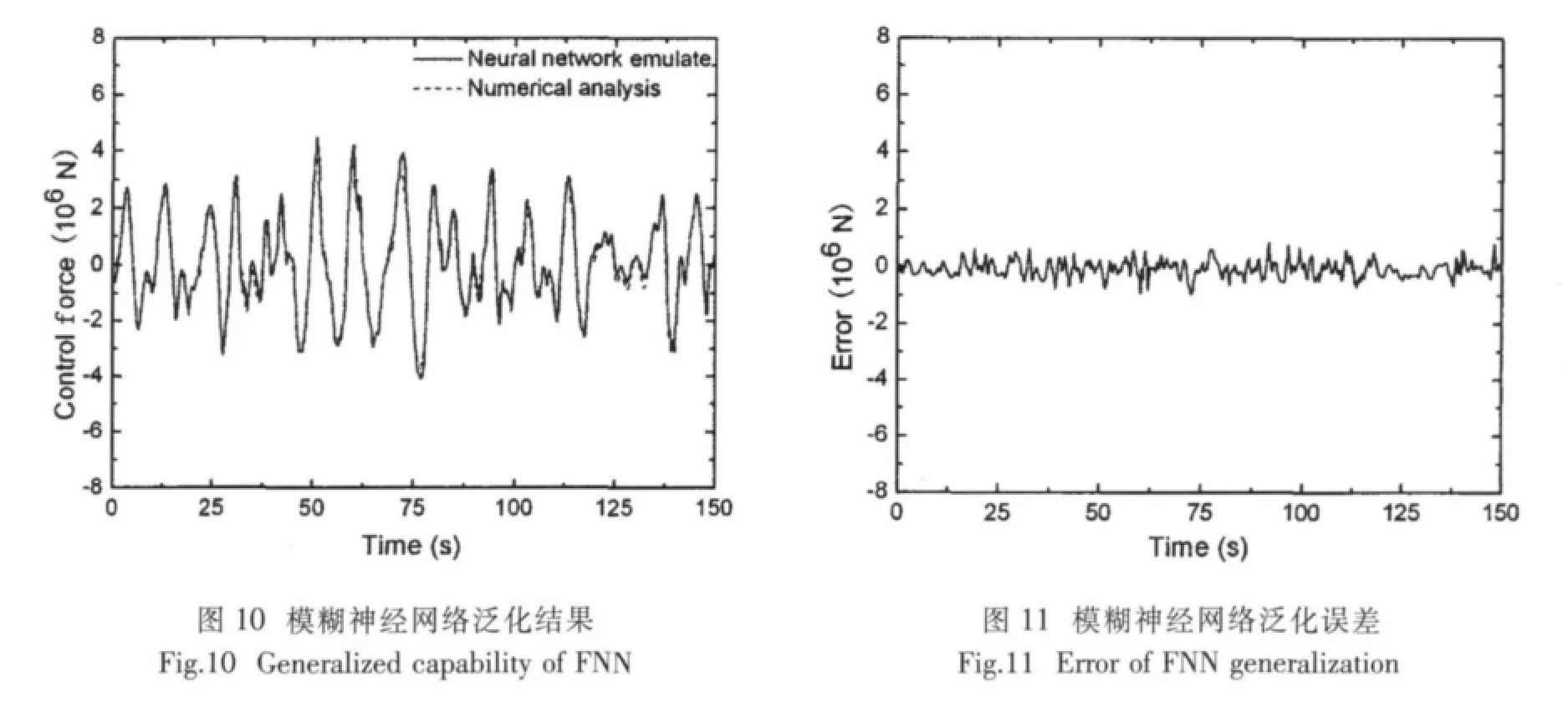
本文用4 000组样本数据对模糊神经网络进行离线训练，经过训练后用1 500组数据检验模糊神经网络的泛化结果，如图10所示。图11为模糊神经网络的泛化误差。从图10和图11中可以看出模糊神经网络具有很好的预测和泛化能力。

表2 计算时间比较Tab.2 Comparison of calculation time

4.4 随机波浪力作用下的导管架式海洋平台主动控制

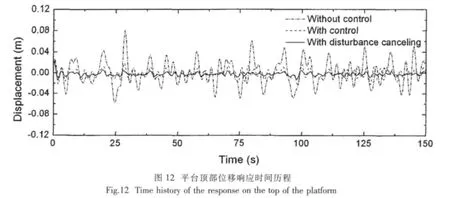
图12中给出了0-150s导管架式海洋平台在随机波浪力作用下及经过控制后的平台顶部的位移响应幅值时程曲线，未控制前位移响应幅值在-0.058 4m至0.080 4m之间，如图中点划线所示。通过基于动态刚度阵法的模糊神经网络自适应预测逆控制后，其顶部位移响应幅值被控制在-0.022 7m至0.020 6m之间，最大位移响应幅值减小达72%，控制效果明显，如图中虚线所示。图中实线表示经过扰动消除后的位移响应幅值，平台顶部位移响应幅值被控制在-0.012 2m至0.005 8m间，最大位移响应幅值减小85%，如图中实线所示。可见通过扰动消除后，对导管架式海洋平台的控制效果更佳。

4.5 随机风扰动的导管架式海洋平台主动控制

在实际海洋环境中，导管架式海洋平台除了受随机波浪力作用，还要受到风等载荷的作用。因此为了进一步验证本文控制模型在遭遇随机风载荷干扰时的抗干扰能力，在导管架式海洋平台顶部作用一个如图13所示的随时间变化的随机风载荷干扰。脉动风速的时程用线性滤波法中的自回归（Auto-Regressive，简记为AR）模型来模拟[11]，其中10m高程标准风速为25m/s，脉动风速的功率谱密度函数采用我国随机风载荷规范中规定的Davenport谱，地形地貌为A类[12]，然后通过Bernoulli方程求得时程风载荷。

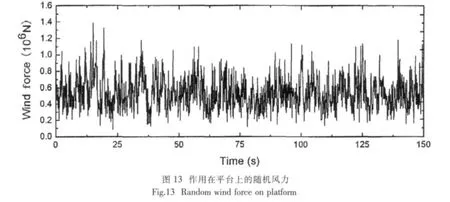
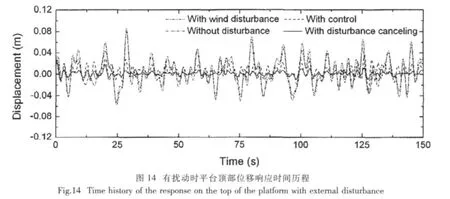
在图13所示随机风力作用下，平台顶部位移响应幅值及经过控制后的位移响应幅值时程曲线如图14所示。从图14中可以看出，只有波浪力作用的平台顶部位移响应幅值时程曲线为图中单点划线所示，有随机风扰动情况下平台顶部的位移响应幅值发生明显改变，平台顶部位移响应幅值在-0.053 60m至0.086 38m之间，图中双点划线所示。图14中虚线表示经过基于动态刚度阵的模糊神经网络预测逆控制器控制后的平台顶部位移响应幅值时程曲线，平台顶部位移响应幅值被控制在-0.029 27m至0.034 70m之间，最大位移响应幅值减小60%，实线为有扰动消除后的控制结果，平台顶部位移响应幅值在-0.010 19m至0.017 99m之间，最大位移响应幅值减小80%。从图中可以看出：对于随机风扰动，未进行扰动消除的控制效果并不很好，而经过扰动消除后，平台的顶部的位移响应幅值得到更为有效的控制。因此可见，采用本文的控制模型可以很好避免扰动对被控平台系统动态响应的影响，具有很强的抗干扰能力。

5 结 论

本文提出了基于动态刚度阵的模糊神经网络自适应预测逆控制模型，并将该模型用于导管架式海洋平台的主动控制中，通过数值算例可以看出：通过动态刚度阵法对导管架式海洋平台快速而精确的建模，将被控对象模型与智能控制算法结合在一起，弥补了模糊神经网络控制中精确的模型特征不能得到应用的不足。由于模糊神经网络有强的预测和辨识的能力，所以通过模糊神经网络预测平台顶部的控制力，有效地克服了控制过程中存在的时滞对控制系统性能的影响；自适应逆控制是将被控系统动态性能和扰动的控制分开来处理，这样可以尽量提高两个控制器的控制性能，而且对于存在随机的风扰动情况也有很好的控制能力；本文将对平台建模、辨识和控制过程中存在的误差当作扰动来处理，这样减小了建模、辨识和控制过程中存在的误差对控制性能的影响。

[1]周亚军,赵德有.海洋平台结构振动控制综述[J].振动与冲击,2004,23(4):40-43.

[2]Kolousek V.Dynamics in engineering structures[M].London:Butterworths Inc.,1973.

[3]周 平,赵德有.动态刚度阵法在船舶总振动计算中的应用[J].船舶力学,2006,10(4):126-132.

[4]Leung A Y T.Dynamic stiffness method and substructures[M].New York:Springer,1993.

[5]王勖成,邵 敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,2001.

[6]Wittrick W H,Williams F W.A general algorithm for computing natural frequencies of elastic structures[J].Quarterly Journal of Mechanics and Applied Mathematics,1971,24(3):263-284.

[7]卢志刚,吴士昌,于灵慧.非线性自适应逆控制及其应用[M].北京:国防工业出版社,2004.

[8]Widrow B,Walach E.Adaptive Inverse Control[M].New Jersey:Prentice-Hall Inc.,1996.

[9]王士同.模糊系统、模糊神经网络及应用程序设计[M].上海:上海科学技术文献出版社,1998.

[10]聂 武,刘玉秋.海洋工程结构动力分析[M].哈尔滨:哈尔滨工程大学出版社,2002.

[11]舒新玲,周 岱.风速时程AR模型及其快速实现[J].空间结构,2003,9(4):27-32.

[12]王修琼,崔剑峰.Davenport谱中系数K的计算公式及其工程应用[J].同济大学学报,2002,30(7):849-852.

Adaptive predictive inverse control for offshore jacket platform

CUI Hong-yu,HONG Ming,ZHOU Ping,ZHAO De-you
(Department of Naval Architecture,Dalian University of Technology,Dalian 116085,China)

A new active control scheme of fuzzy neural network(FNN)adaptive predictive inverse control(APIC)for jacket offshore platforms based on dynamic stiffness matrix(DSM)method is presented.The pressure transducers which are placed on the leg of the offshore platform are used for measuring the random wave forces in real time.And then the responses on the top of the platform under these random wave forces are calculated quickly and accurately by the DSM method.The calculated responses are taken as the input signals of FNN adaptive predictive inverse controller,through which the control force in the imminent time to the platform is forecasted.Meanwhile,a feedback adaptive predictive inverse controller is designed for the purpose of disturbance canceling and error reduction.For validation of the anti-disturbance capability of the control scheme,the active control of the jacket platform with external disturbances of random wind loads was also investigated.The numerical results show that the proposed control scheme has excellent anti-disturbance capability,and can overcome the time delay,and can decrease the vibration response of jacket offshore platform.

offshore jacket platform;dynamic stiffness matrix;adaptive predictive inverse control;

P751 TP181

A

1007-7294（2011）05-0545-11

2010-01-10 修改日期：2010-07-11

国家自然科学基金资助项目（50908036）

崔洪宇（1977-），男，博士后，E-mail:chy_2008@hotmail.com。