平面状态下EWK延性断裂准则与K准则对比研究

杨锋平，孙 秦，罗金恒，张 华，张 奕

（1中国石油集团石油管工程技术研究院，石油管力学和环境行为重点实验室，西安 710065；2西北工业大学 航空学院，西安 710072）

平面状态下EWK延性断裂准则与K准则对比研究

杨锋平1，孙 秦2，罗金恒1，张 华1，张 奕1

（1中国石油集团石油管工程技术研究院，石油管力学和环境行为重点实验室，西安 710065；2西北工业大学 航空学院，西安 710072）

为研究EWK延性断裂准则对金属起裂及扩展的预测能力，将EWK断裂算法嵌入ABAQUS主程序。针对金属I型裂纹，在平面应变条件下，通过试验与有限元计算相互对比的方法，研究了该准则与应力强度因子K准则对紧凑拉伸CT试样起裂的预测结果，发现两者有近似等效性。在平面应力条件下，以紧凑拉伸CS试样为模型，通过有限元计算，提取由EWK控制断裂的结构KR-曲线，将该曲线与试验资料对比，发现两者吻合良好。

EWK延性断裂准则；应力强度因子；KR-曲线；有限元方法

1 引 言

金属材料断裂往往是一种弹塑性断裂，相关研究工作非常多见。按理论归类，这些工作主要集中在以下三类：第一、以古典强度理论为依据。这部分内容非常丰富，中文可参考俞茂宏教授的论文[1]或

专著[2]；第二、以断裂力学的应力强度因子和J积分等为理论依据；第三、以损伤力学为理论依据。三者特别是前两者为许多工程问题的解决提供了强有力的支持，而第三者则正在成为更好的理论。三者各自的缺陷在于，古典强度理论对材料进行了理想化的假设，对断裂的研究大部分停留在经验上。断裂力学有比较完善的理论体系，但其研究对象是含裂体，且对裂纹作了理想化的假设。对于实际结构从无初始裂纹开始断裂或含复杂形状裂纹的问题则无能为力。损伤力学由50年代前苏联学者Kachanov提出雏形，其发展特别是连续损伤力学（CDM）的发展是在70年代由Lemaitre教授[3]领导完成。宏细观结合的损伤力学被认为是研究断裂最有前途的方法，不过就目前而言，损伤因子的演化方程一直是理论与试验亟待突破的瓶颈。

基于理论一或三的一类重要工程应用是各种金属延性断裂准则，主要解决无初始裂纹结构的开裂问题，在金属成型等领域起着重要作用。如何评定某种准则的精确程度成为其控制断裂的关键，目前较为多见的方法是通过几类不同的试验[4-10]，包括不同尺寸的镦粗、拉伸试验，然后建立试验的有限元模型，将基于该延性断裂准则的计算结果与试验对比，以此确定这种延性断裂准则的优劣，本文作者也研究过此类方法。该方法的不足之处在于其判定的依据仅来自有限的几类试验，无法从理论上获得更多的支持。

由于断裂力学有比较完善的理论基础，若某种延性断裂准则的判定结果与断裂力学的判定结果一致，则说明该准则与断裂力学K或J准则等效，从而获得了一定的理论支持。在等效关系确立后，可进一步认为对于K准则或J准则无法解决的问题（例如无初始裂纹结构开裂问题），可以试图用该延性断裂准则解决，当然其最终结果需要试验评定。这样做的实质是把基于古典强度理论或损伤力学理论的金属延性断裂准则与断裂力学理论结合在一起考虑，充分发挥了各自的优势，使得到的结论更加合理。然而很少有学者在同样的结构中将两者一起对比，本文的研究工作即在于此。通过两种紧凑拉伸试样（两类模型均满足小范围屈服假设，金属小范围屈服仅表示塑性区范围较小，但塑性区内变形仍非常剧烈，材料断裂属于韧性断裂），将Kamoulakos博士提出的EWK延性断裂准则[11]与K准则对比。结果证实了EWK准则与K准则有较好的互换性。

2 EWK断裂模型

EWK模型是Kamoulakos博士在McClintock、Wilkins（主要贡献）等人的工作基础上加以总结，在假设裂纹形成和扩展是材料一个连续特性的前提下，认为结构断裂是材料应变损伤的累积结果。裂纹的起始、扩展和结构的断裂主要取决于危险区域现时和历史的受力情况，独立于危险区域的形状、边界条件，除非危险区域的形状和边界条件影响着它的受力情况。他给出公式如下：

当材料中某个点的损伤变量Dp值达到临界值时，以该点为中心的某个局部区域（半径为Rc的圆）断裂失效。式中εp表示等效塑性应变，p代表该点所受的静水压力，Si表示应力偏量；α、β为材料常数，分别代表拉、剪对材料微孔洞生长的影响因子，plim表示不考虑孔洞效应时的理想极限静水压力，为材料常数。该模型与损伤力学概念的区别之处在于，认为损伤变量Dp的演化不影响材料的本构关系。因为从表达式看，Dp是由代表外力作用因素的量（w1代表拉、w2代表剪）构成，而不是由诸如材料微孔洞面积等内部因素构成，因此它不影响本构曲线。微孔洞的生长等材料内部因素则由α、β确定，认为是材料常数。从断裂力学角度考虑，Dp具有应变能密度性质，一定程度上和断裂力学中的能量释放率理论吻合。从古典强度理论体系出发，也可将其仅仅理解为与第二强度理论等相似的一种理论，区别在于EWK表达式是一种积分。该理论涉及的4个材料常数Dp、α、β、plim可由4种断裂实验确定。本文以铝合金2A12-CZ（LY12-CZ）为材料，分别进行如图1所示5种试验以确定材料常数（α试验为了得到材料本构关系）。 由试验确定的该材料常数分别为：Dp=0.234 6，α=2.311 0，β=-0.385 7，plim=1 717MPa。

在有限元计算时，EWK算法的实现是基于单元积分点计算的。将自行编制的EWK断裂子程序嵌入ABAQUS主程序中。对于每个单元的每个积分点，主程序每完成一次增量步计算，子程序提取一次EWK判断准则需要的参数，并进行判断，若达到断裂门槛值，积分点杨氏模量置零，否则不作任何变化。遍历所有单元的积分点后，程序进行下一个增量步计算。这样保证了主、子程序之间的实时通信，直到外载全部添加完毕为止。算法流程图如图2所示，该算法将使断裂发生在单元上，故单元越小，其计算所得的结果越精确，但它对单元的形状没有任何要求。另外，只要计算收敛，该算法可一直进行到裂纹扩展完毕。

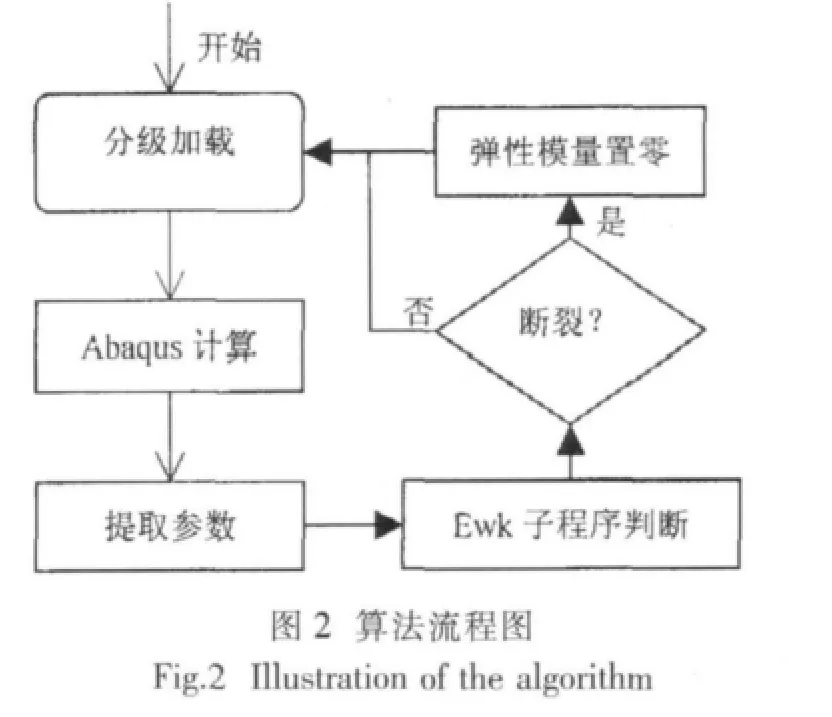
3 紧凑拉伸（CT）试样模拟

3.1 方法

该模型目的在于考察K准则与EWK准则的关系。K准则对于弹塑性断裂的有效性仅仅限于小范围屈服。因此，为了保证裂纹顶端处于小范围屈服条件，标准CT试样（其试样设计以及结果评定都需要核实小范围屈服及平面应变条件）是可靠的。用标准CT试样可以得到材料的断裂韧性KIC。反过来说，如果用测得的KIC值（一般需要用有效裂纹长度修正后的K准则）来预测CT试验的P-V曲线，其预测结果应当与试验曲线一致。若采用EWK准则预测，如果其预测所得的P-V曲线也与试验曲线一致，则证明了在小范围屈服条件下，EWK与K准则有等效性；如果不一致，则说明EWK准则的预测能力在材料小范围屈服条件下没有很好的精度。因此，本节通过试验与基于EWK准则的有限元模拟对比的方法来确认上述思想。

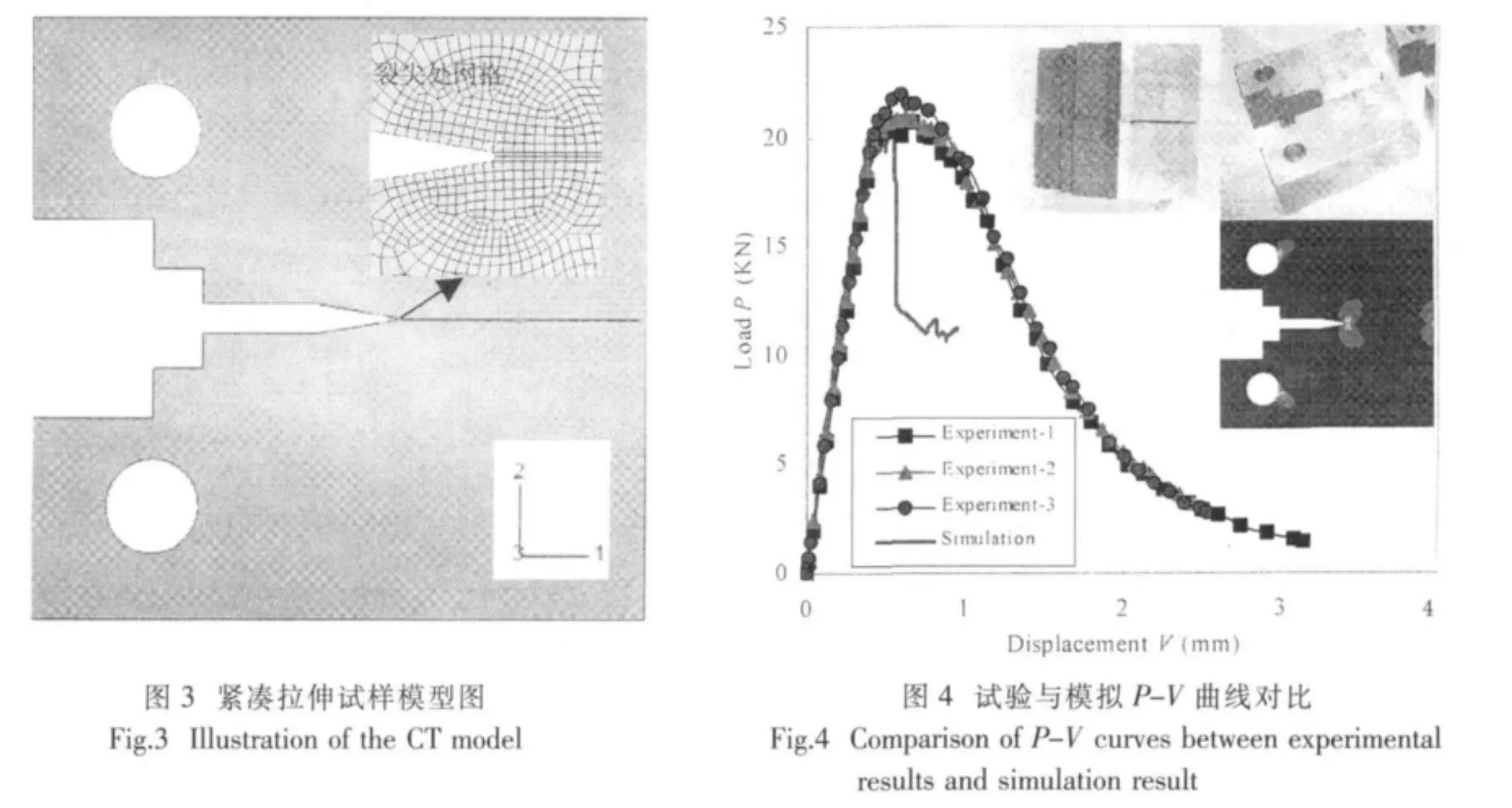
试验依据HB5142-96，试样厚度B取25mm，宽厚比W/B=2。有限元计算时材料模型使用图1(a)所得的本构关系，其真实应力应变曲线特征数据如下：弹性模量71 200MPa，泊松比0.33，屈服应力380MPa，极限应力590MPa，最大应变0.15。裂尖模型建成半径为0.08mm的半圆，裂尖局部细化网格，使最小网格尺度为0.1mm。采用8节点平面应变单元。分别在模型的两个销轴孔处添加1mm的位移载荷，并在模型对称轴处约束好1方向的位移，如图3所示（线切割及疲劳裂纹建成了开口裂纹）。试样断口及测得的P-V曲线取部分点如图4“Experiment”所示。有限元计算在断裂处理上采用1节中的办法，单元变刚度引起的收敛性问题可参看文献[12]。计算一直持续到载荷加载完毕或计算不收敛，其结果如图4的“Simulation”所示。

3.2 结果及讨论

对于平面应变的应力条件（厚板）而言，一旦起裂，则迅速达到失稳扩展，而不像薄板那样起裂后还可继续承载。因此对于图4中的曲线，以最大载荷为界限，只有前半段曲线对KIC计算有意义。对于前半段曲线的线性段，有限元模拟比试验略显刚硬，约2%。原因与计算采用平面应变单元有关。因为真正试验中，试样只有沿厚度方向正中间一层才处于纯粹平面应变状态，其上下两个表面均处于纯粹平面应力状态，沿厚度方向中心向两边是一种平面应变状态向平面应力状态的过渡。当然这种过渡剧烈，使得绝大部分处于近似的平面应变状态。而有限元模拟将这“绝大部分”变成了“全部”，于是显得有些刚硬。有限元计算所得的最大载荷则显示了该延性断裂准则的精度。由曲线可以看出，三件试样所得最大载荷均值为21.41kN，有限元计算所得最大载荷为20.90kN，相对误差2.38%。这种考察精度的缺点在于忽略了实际裂纹长度的影响。有限元建模时取裂纹长度a′=0.5W=25mm，实际试件在疲劳裂纹预制时不可避免会有长有短，本试验三个试样的裂纹长度分别为25.29mm、24.00mm、24.57mm。

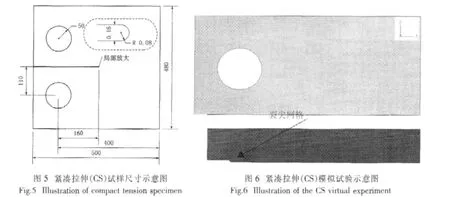
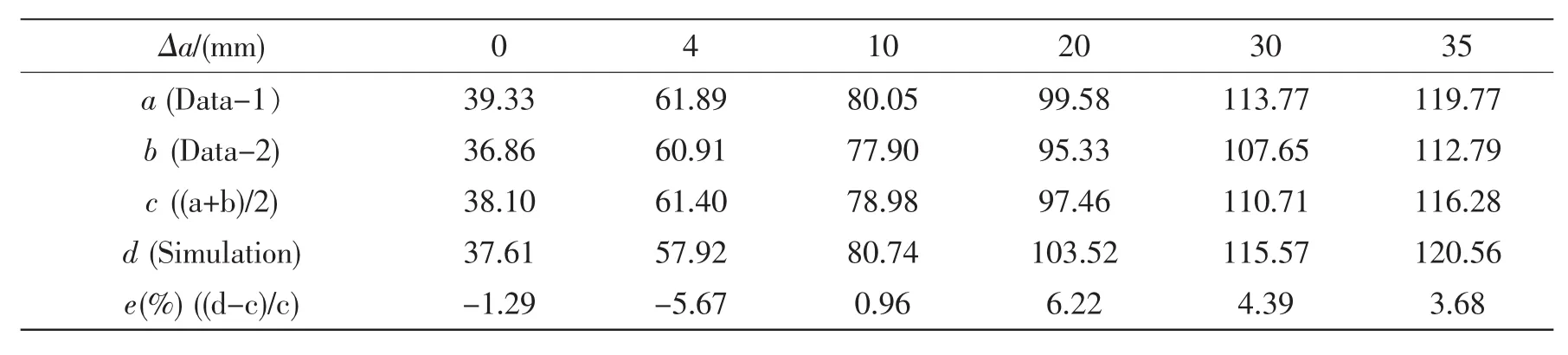
为了避免裂纹长度的影响，还可从另一个种更加客观的角度去评价其精度，即：真实试验可以得到这种材料的平面应变断裂韧性KIC，而基于EWK断裂子程序的有限元计算可看成一种虚拟试验，通过这种虚拟试验也可计算得到这种材料的平面应变断裂韧性KIC′。于是可通过KIC与KIC′的接近程度来考察EWK延性断裂准则的精度。根据HB5142-96数据处理方法，可得三件试样所得KIC分别为34.15MPa·m1/2、31.82MPa·m1/2、34.85MPa·m1/2，且三组数据均有效，均值 KIC为 33.61 MPa·m1/2。 对于虚拟试验，条件载荷 PQ′=20.05kN，最大载荷 Pmax′=21.41kN，载荷比 Pmax′/PQ′=1.04<1.1，裂纹长度 a′=25mm，计算得 KIC′的条件值 KQ′=34.65MPa·m1/2，计算 2.5(KQ′/σs)2=20.78

4 紧凑拉伸（CS）试样模拟

4.1 方法

本节目的在于考察平面应力条件下K准则与EWK准则的关系。当试样厚度足够大，三维约束已经达到平面应变条件时，断裂韧度KIC是与厚度B和裂纹扩展量Δa无关的材料特性。但当试样厚度很薄，塑性区尺寸与厚度相比不再是很小，则裂纹尖端应力应变场将处于平面应力状态。与平面应变断裂问题相比，平面应力断裂问题更为复杂。其主要原因在于材料起裂后，结构并未马上进入失稳，而是可以继续承受载荷而出现缓慢、稳态的扩展。在这种情况下，材料的抗裂阻力（R）既与结构厚度有关，又与裂纹扩展量Δa有关。对于给定厚度而言，测量K-Δa曲线成为衡量结构断裂韧性的一种办法。

于是为了评价在平面应力条件下EWK断裂算法的准确性，可将给定材料给定厚度的标准试样用基于EWK断裂准则的有限元算法计算其断裂过程，将计算得到的K-Δa曲线与真实试验所得曲线对比，若两者符合较好，则说明EWK断裂算法在平面应力条件下有较好精度。为此，采用HB5261-83金属板材KR-曲线试验方法中的标准紧凑拉伸试样，取厚度B=2mm，宽度W=400mm，初始裂纹a0=160mm，如图5所示。裂纹尖端建成半径为0.08mm的半圆模型，此举既模拟了裂尖的钝化效果，又可使划分网格时避免应力奇异。有限元计算时取其一半模型，将对称线上沿2方向的位移约束，销钉孔加拉力载荷，同时为约束1方向运动，将对称线上远离裂尖的地方添加1方向约束。模型采用4节点平面应力单元，在裂尖以及裂纹可能扩展的路径上细化单元，使其最小尺寸为0.1mm（基本为肉眼可见最小裂纹的尺寸），以保证获得较为精确的K-Δa，如图6所示。材料的本构关系采用2节中的数据。

4.2 结果及分析

有限元计算时，有效裂纹增量的计算根据HB5261-83“有形裂纹长度加塑性区修正量”方法可得如下

其中da表示当前可见裂纹扩展量，即模型中单元丢失的长度，ry表示裂纹前沿塑性区修正量，可用以下公式计算：

其中KI指当前的应力强度因子。KR的获取也可根据HB5261-83中提供的方法，即

其中P表示当前所加的载荷量，可由约束端沿2方向的支反力求出；F （a/W） 表示形状系数，可由以下公式计算：

其中a表示有效裂纹长度，其计算表达式如下

由此可知，此方法中Δa的计算依赖于当前的KR值，而KR的计算又依赖于当前的Δa值，这就形成一对矛盾。解决该矛盾可采用迭代求解，即取很小的增量步，利用上一步的Δai-1值，根据公式（8）算得当前步 KR(i)值，然后根据公式（7）、（6）求解当前步的 Δai，再利用当前步 Δai，求解下一步 KR(i+1)。 在第一步 KR(1)的计算中，可认为上一步 Δa0=0。 将得到的数据点（Δai，KR(i)）每十个取一个如图 7“simulation”所示。并将其拟合成函数，外推至Δa0=0，可得图7曲线“Fitting of simulation”。真实试验拟合所得的KRΔa 曲线如图 7“Data-1”、“DATA-2”所示，其数据源自文献《中国航空材料手册（第三卷）》[13]，列出 6 个数据点的信息见表1。

表1 试验及模拟所得某些裂纹扩展阻力值KR/MPa·m1/2Tab.1 Some resistance values of crack propagation given by tests and simulation,KR/MPa·m1/2

在认为试验可靠的前提下，将模拟数据与试验所得两组数据的均值做相对误差分析，其值可见表1的最后一行。最大相对误差出现在Δa=20mm处，即出现在曲线的中部，为6.22%，最小相对误差为0.96%，出现在裂纹扩展量Δa=10mm处，起裂时，其相对误差为1.29%，6个数据点平均误差为3.70%。这些数据说明，基于EWK断裂准则对平面应力条件下薄板断裂韧性的预测有很好的精度。

5 结 论

（1）平面应变条件下，通过数值计算与试验对比的方法确立了EWK延性断裂准则与K准则之间存在近似等效关系。

（2）平面应力条件下，EWK准则预测裂纹稳态扩展所获得的KR-曲线与现有试验数据吻合较好。

[1]俞茂宏.强度理论百年总结[J].力学进展,2004,34(4):529-560.

[2]俞茂宏.双剪理论及其应用[M].北京:科学出版社,1998.

[3]Lemaitre J,Desmorat R.Engineering Damage Mechanics[M].Berlin:Springer,2005.

[4]虞 松,陈 军,阮雪榆.韧性断裂准则的试验与理论研究[J].中国机械工程,2006,17(19):2049-2052.

[5]Venugopal Rao A,Ramakrishnan N,Krishna kumar R.A comparative evaluation of the theoretical failure criteria for workability in cold forging[J].Journal of Materials Processing Technology,2003,142:29-42.

[6]Ozturk F,Lee D.Analysis of forming limits using ductile fracture criteria[J].Journal of Materials Processing Technology.2004,147:397-404.

[7]Clift SE,Hartley P,Sturgess C E N,Rowe G W.Fracture prediction in plastic deformation process[J].Int.J Mech.Sci.1990,32:1-17.

[8]Bao Y B,Wierzbicki T.A comparative study on various ductile crack formation criteria[J].Journal of Engineering Materials and Technology,2004,126:314-324.

[9]Narayana Murty S V S,Nageswara Rao B,Kashyap B P.Improved ductile fracture criterion for cold forming of spheroidised steel[J].Journal of Materials Processing Technology,2004,147:94-101.

[10]Gouveia B P P A,Rodrigues J M C,Martins P A F.Ductile fracture in metalworking:experimental and theoretical research[J].Journal of Materials Processing Technology,2000,101:52-63.

[11]Kamoulakos A.The ESI-Wilkins-Kamoulakos(EWK)rupture model[M].In:Raabe D,ed.editors.Continuum Scale Simulation of Engineering Materials.Berlin:Wiley-VCH,2004:796-804.

[12]杨锋平,孙 秦.韧性金属材料渐进断裂的有限元算法研究[J].金属学报,2008,44(4):489-494.

[13]颜鸣皋,刘伯操,李金桂等.中国航空材料手册（第三卷）[M].北京:中国标准出版社,2002:39-83.

Studies on comparison between EWK ductile criterion and K criterion in plane state

YANG Feng-ping1,SUN Qin2,LUO Jin-heng1,ZHANG Hua1,ZHANG Yi1
(1 The Key Laboratory for Mechanical and Environmental Behavior of Tubular Goods,CNPC Tubular Goods Research Institute,Xi’an 710065,China;2 School of Aeronautics,Northwestern Polytechnical University,Xi’an 710072,China)

In order to study the precision of EWK ductile criterion for mode I cracking of metallic material,a subroutine of EWK fracture criterion was programmed and added to ABAQUS’main program.For 2A12-T4 aluminum alloy,under the stress condition of plane strain state,this criterion was compared with K-Criterion in the initial cracking prediction of compact tension specimen.Through comparison of experimental result and FEM result,it is found that EWK criterion and K-Criterion are approximatly equivalent.Under the stress condition of plane stress state,another compact tension specimen was taken as computational model whose cracking was judged by EWK criterion.KR-curve was derived after this computation was complete.It shows that the KR-curve is close to the published experimental data.

EWK ductile criteria;stress intensity factor(SIF);KR-curve;finite element method(FEM)

TB125

A

1007-7294（2011）05-0506-07

2010-05-10

杨锋平（1982-），男，博士，中国石油集团石油管工程技术研究院工程师；

孙 秦（1956-），男，西北工业大学教授，博士生导师。