一种适合线划图坐标系统转换的方法

陶叶青，杨 娟，方 刚

（宿州学院地球科学与工程学院，安徽 宿州234000）

一种适合线划图坐标系统转换的方法

陶叶青，杨 娟，方 刚

（宿州学院地球科学与工程学院，安徽 宿州234000）

对旧坐标系统下线划图的利用，关键在于对原有线划图的坐标系统进行转换，通常选用的转换方法是在平面上进行．基于平面的线划图转换方法易于实现，但也具有一些局限性．分析得出当前线划图坐标系统转换方法具有不同区域的长度变形使得尺度比参数无法统一、不便于地方独立坐标系下的线划图向国家坐标系进行转换这两方面的局限性，提出在椭球面上实现对线划图坐标系统进行转换，并给出以大地元素为转换参数的数学转换模型和转换方法．

线划图；坐标系统转换；长度变形；邻带坐标换算；大地元素

1 引 言

线划图作为测绘工作的重要成果，在不同坐标系统更替的过程中，如何实现对已有资料的再利用，是测绘工作者关心的问题．通常采用的方法是对原有线划图的坐标系统进行转换，但转换精度影响线划图的使用．因此，对于线划图的转换方法进行讨论有一定的实用价值．论文对传统线划图坐标系统转换原理与方法进行阐述，分析当前线划图坐标系统转换方法的不足之处，给出以椭球面为基准面实现对线划图坐标系统进行转换的数学模型与方法，并比较与传统转换方法的优缺点．

2 基于平面的线划图坐标系统转换

2．1 转换的原理与方法

在平面坐标系统中，对线划图进行转换，一般包含四个转换参数，即两个平移参数（a，b）、一个旋转参数α、一个尺度参数λ．最常见的转换过程有两个［1］：先旋转、再平移、最后统一尺度；先平移、再旋转、最近统一尺度．虽然转换过程不同，求得的四个转换参数也不相同，但是它们最终的转换结果都是一致的，按第一种转换过程进行，其数学转换模型为［2］：

其中（x1，y1）、（x2，y2）分别为不同坐标系统下的坐标．上述转换模型转换参数的求解，可通过在不同坐标系下进行控制测量，获得公共点在不同坐标系中的坐标 （表1），按最小二乘法求得转换模型的四个参数，即两个平移参数（a，b），一个旋转参数α，一个尺度参数λ．基于平面的划线图转换可通过CAD软件相应平移、旋转、伸缩命令实现 （图1）．

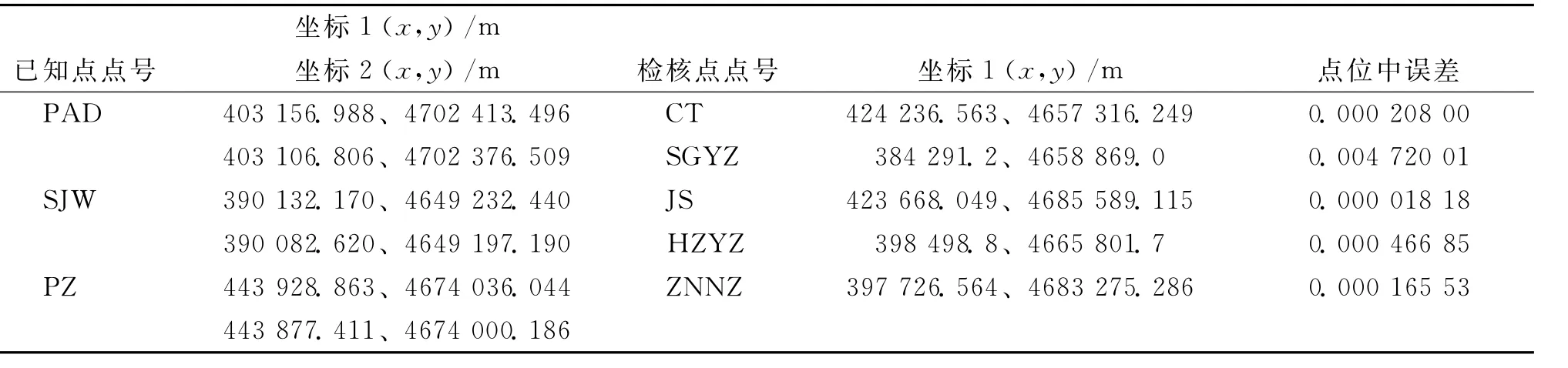
表1 公共点求解转换模型参数

图1 CAD实现对线划图坐标系统的转换

2．2 转换方法的缺点

2．2．1 无法顾及长度变形对尺度比参数的影响

线划图坐标系统转换的精度，除受转换模型参数求解精度的影响外，还受到投影因素的影响 （以正形投影为例）．正形投影使得观测点在椭球面上的大地坐标（B，L）表现在线划图中的平面坐标（x，y）会有长度变形，且变形的尺度与距离中央子午线的距离有关［3］：

式中y为横坐标，距离中央子午线越远的点，其绝对值越大．R为地球平均曲率半径．同一幅线划图中，处于不同区域的观测点距离中央子午线的远近不同，其相应的长度变形显然是不同的．长度变形反映在平面坐标系统转换的数学模型中 （式1），则是尺度比参数．在转换模型中，尺度比参数是通过若干个公共点坐标求得．公共点求解所得的尺度比参数，只是代表其自身的点位属性．对于处在不同区域的观测点，有别于求解模型参数的公共点，其长度变形不一至引起尺度比参数无法统一．采用同一尺度比参数进行转换，对转换后线划图的点位精度有一定影响．

2．2．2 不便于地方独立坐标系下的线划图向国家坐标系转换

国家坐标系采用分带投影的方法，使得靠近投影带边缘地区出现较大的长度变形．为使测量成果能够更好的满足本地区建设生产的需要，很多地区都定义地方独立坐标系．地方独立坐标系的定义通常有三种方法，为了便于地方独立坐标系向国家坐标系转换，同时减小长度变形，通常采用任意带投影［4］，即选用经过本地区中心位置的经纬为中央子午线，坐标系的定位与定向与国家坐标系一致．采用任意带投影的地方独立坐标系向国家坐标系的转换，通常运用高斯邻带换算［4］方法实现，即更改投影区域的中央子午线．线划图作为表述在平面上的地图要素矢量数据集［5］，无法在平面上直接通过高斯邻带换算实现坐标系统的转换．

3 基于椭球面的线划图坐标系统转换

3．1 转换的原理与方法

对于上文分析得出的结论，传统线划图坐标系统转换的缺点主要有：无法顾及长度变形对尺度比参数的的影响，使得转换模型中采用同一尺度比参数对转换精度有影响；不便于地方独立坐标系下的线划图向国家坐标系转换．上述两点缺点是由于坐标系统转换方法以平面为基准，通过实现对平面坐标（x，y）的转换而产生．鉴于此，如果以椭球面为线划图坐标系统转换的基准面，以大地元素作为转换参数，可以克服传统转换方法的不足之处．

在椭球面上实现对线划图坐标系统的转换以参考椭球面为基准，采用两个以上公共点在不同坐标系下的子午线弧长之差（ΔX）、平行圈弧长之差（ΔS）、大地方位角之差（ΔA）、大地线长度之比（λs）为转换参数，其中（ΔX）、（ΔS）为移动参数、（ΔA）为旋转参数、（λs）为尺度比参数．定义数学转换模型为：

具体转换步骤为：

（1）进行控制测量，获得两个以上公共点分别在不同坐标系统下的大地坐标（B1，L1）、（B2，L2）．

（2）根据大地坐标计算公共点间的子午线孤长之差（ΔX）、平行圈弧长之差（ΔS）、大地方位角之差（ΔA）、大地线长度之比 （λs）．

（3）以转换之前线划图坐标系统对应的参考椭球为投影面，将线划图按投影反算［5］，由平面投影至椭球面 （图2、图3）．

（4）以大地元素为参数的数学模型 （式3）为转换模型，按先旋转、再移动、最后统一尺度，进行线划图坐标系统转换．

（5）将转换后线划图以转换后坐标系统对应的参考椭球为投影面，按投影正算［5］，由椭球面投影至平面．

图2 投影反算前的线划图

图3 投影反算后的线划图

3．2 算例与结论

应用2．1节给出的已知数据，对已知点的两套平面坐标分别进行高斯反算，并按3．1节中给出的转换方法与步骤，求解基于大地元素的转换模型参数．将检核点的已知平面坐标进行高斯反算，得到检核点的大地坐标，与应用式 （3）求出的大地坐标作差（ΔB，Δl），以式 （4）作为精度衡量标准：

已知点、检核点的点位分布如图 （1）所示，表 （2）给出已知点、检核点的大地坐标，以及通过大地元素在椭球面上实现坐标系统转换的精度．

表2 通过大地元素实现坐标系统的转换

通过表 （2）与表 （1）的对比可以得到，以大地元素为转换参数，基于椭球面实现对线划图坐标系统的转换能够满足传统转换方法对转换精度的要求．基于椭球面的线划图坐标系统转换方法的优点在于能够克服传统转换方法的不足之处，顾及了由于投影引起的长度变形对尺度比参数的影响、便于地区独立坐标系下的线划图向国家坐标系的转换．但相比较于通过平面实现线划图坐标系统转换方法，基于椭球面的转换方法有计算量大、转换过程烦琐、等不足之点．以大地元素为转换模型的参数，它们在数值上都表现为微小量，因此通过矩阵变换求解参数时，容易引起舍入误差、产生病态矩阵．基于椭球面的转换方法不足之处在实际转换过程中应给予重视，这也是下一步研究工作需要解决的问题．

［1］ 姚宜斌．平面坐标系统相互转换的一种简便算法 ［J］．测绘与信息工程，2001，（01）：1－4

［2］ 施一民．现代大地控制测量 ［M］．北京：测绘出版社，2003：20－60

［3］ 陶本藻，邱卫宁，黄加纳，等．误差理论与测量平差基础 ［M］．武汉：武汉大学出版社，2003：5－32

［4］ 孔祥元，郭际明，刘宗泉．大地测量学基础 ［M］．武汉：武汉大学出版社，2005：36－55

［5］ 胡鹏，黄杏元，华一新．地理信息系统教程 ［M］．武汉：武汉大学出版社，2002：1－15

Method for Line Map Coordinates System Conversion

TAO Ye－qing，YANG Juan，FANG Gang
（Earth Science and Engineering School of Suzhou University，Suzhou 234000，Anhui，China）

To use line map of old coordinates system，the key point is that line map of coordinates system should be converted．And the method of conversion is done by plane usually．Although the method of line map coordinates system conversion based on plane is easy to achieve，it has some limitations：the current localizations，such as different area distortion of distance makes scale－ration different，and inconvenient conversion of local coordinate system．Opinion of plane map coordinates system conversion based on ellipsoid is put forward．Besides，geodetic elements as the parameters of mathematical model and conversion method are given．

line map；coordinates system conversion；distortion of distance；computation of coordinate zonal；geodetic elements

P 282

A

1673－1492 （2011）06－0032－04

来稿日期：2011－08－29

安徽省教学研究项目 （20101073）；宿州学院硕士科研启动基金的资助 （2010yss05，2010yss06）

陶叶青（1984－），男，江苏淮安人，宿州学院地球科学与工程学院讲师，硕士．

刘守义 英文编辑：刘彦哲］