新的RSA－TBOS广义签密方案

王会歌，曹 浩，刘 斌，庄锁法，沈 峰

（安徽科技学院理学院，安徽 凤阳233100）

新的RSA－TBOS广义签密方案

王会歌，曹 浩，刘 斌，庄锁法，沈 峰

（安徽科技学院理学院，安徽 凤阳233100）

为了抵抗适应性选择消息攻击、提高签名生成效率、加强秘密共享，提出一种新的RSA－TBOS广义签密方案．与韩益亮的广义签密方案相比，本方案是基于RSA大整数分解的困难性，且密钥长度的下限为160bits，能够实现短签密．其计算量大小介于韩益亮的方案和J．Malone－Lee的方案之间．同时，由于方案的签名是两部分消息经过随机化填充后的连接，因此，可以抵抗中间相遇攻击．经过证明，方案IND－CCA2是安全的．

签密；广义签密；数字签名；可公开验证

1 引 言

签密方案是Zheng在文献 ［1］最早提出来的，他在该文献中提出了两个非常类似的签密方案，分别称为SCS1和SCS2，在这两个方案中SCS1虽然在计算和通信带宽方面很有效，但是在安全性方面，因为涉及到消息的保密性，没有给出IND－CCA2安全性的规约证明．在不可否认性质中，该方案没有给出任何零知识证明协议．Zheng之后又出现了许多基于椭圆曲线上的离散对数困难性问题的签密方案［2－6］，虽然这些方案具有很高的效率，安全性也高，但适合于较小的系统．为了满足一些大型系统的需要，近些年来一些人又提出了基于RSA的签密体制．随着RSA加密和签名体制的进一步扩充和完善，它们的安全性和不可否认性也逐步的提高．起初是普通RSA加密、签名体制的研究，后来发展为基于强RSA假设的加密、签名体制［7，8］，但这些方案都没有给出随机预言模型下的安全性分析，在语义上并非安全，只能使用于签名或加密存在的情况下．在文献 ［9］中提出了一种最优非对称加密填充 （RSA－OAEP）方案，该方案给出了基于随机预言模型下形式化的安全证明．文献 ［10］中Malone－Lee等提出了一种RSA－TBOS签密方案．

本文就是以RSA－TBOS为基础提出的一种改进了的广义签密方案，该方案和文献 ［11］提出的方案不同，文献 ［11］中的方案是一种基于椭圆曲线离散对数假设的一种广义签密方案，适合于小型的系统．而本文提出的新的方案是基于大整数分解的困难性而设计的一种广义签密方案．新的方案不但可应用于小系统，而且也可应用于大系统，并且对其进行了效率分析．

2 签密与广义签密的定义

2．1 签密方案的定义

签密是以一种很有效的方式获得数字签名和加密组合功能的公钥密码原型．它能提供三种经常使用的安全性服务：保密性、认证性和不可否认性．执行协议的双方是签密方 （发送方）S和解签密方 （接受方）R．S对消息空间M 中的一则消息m产生签密文，R解出原始消息同时加以验证．类似于签名，发生争议时第三方可以进行仲裁．下面的定义采用文献［11］中的：

定义1 签密方案Σ＝（Gen，SC，DSC）由三个分量组成：

Gen：是密钥生成算法，为用户U产生密钥对，（SDKU，VEKU）←Gen（U，T），T为安全参数，SDKU为用户U的私钥，VEKU为用户U的公钥．

SC：签密生成算法，为概率算法，对于消息m∈M，ω←SC（m，SDKS，VEKR），ω为密文．其中SDKS表示用户S（发送方）的私钥，VEKR表示用户R（接收方）的公钥．

DSC：解签密生成算法，为确定算法，接收者利用自己的私钥和发送者的公钥解签密恢复消息并验证接收消息的正确性．对于签密文ω，m∪｛⊥｝←DSC（ω，SDKR，VEKS），表示验证失败．

定义2 （正确性）签密方案Σ＝（Gen，SC，DSC）是正确的．

对任意的S，R，m∈M ，存在DSC（SC（m，SDKS，VEKR），SDKR，VEKS）＝m ，Zheng给出了签密的安全性概念，一个签密方案是安全的，需要满足如下安全属性：

不可伪造性 （unforgeability）：适应性攻击者 （包括接收者）冒充发送方伪造一则密文在PPT时间计算上是不可行的．

不可否认性 （non－repudiation）：发送方想要否认他曾发出的签密文时，第三方进行仲裁在计算上是可行的．

机密性 （confidentiality）：适应性攻击者 （除发送方和接收方外的任何第三方）想要获得关于明文的部分信息在PPT计算时间上是不可行的．

消息的可认证性 （authentication）：对于发送方发给接收方的任何消息接收方都可以通过消息认证码的形式进行认证．

2．2 广义签密的定义

在一些系统中，有时既要满足机密性和完整性的需要，有时只需要其中之一．这样一来，定义1中的签密方案将不再可行．为了节省空间和执行代价，就需要设计一种满足这三方面要求的多功能系统，这样的方案在文献 ［11］中已经提出，但文献［11］中的方案适合应用于小系统，而本文设计的方案不仅适合应用于小系统，而且适合应用于大系统．

定义3 广义签密方案Σ＝（Gen，SC，DSC）由三个算法组成：

和上面的定义相同，Gen为密钥生成算法．

签密算法SC 为概率算法，对于消息m，ω←SC（m，SDKS，VEKR），当R∈￠时，存在SC（m，SDKS，VEKR）＝Sig（m，SDKS），DSC（ω，SDKR，VEKS）＝Ver（τ，VEKS）；解签密算法 DSC 为确定算法，对于签密文ω，m ∪ ｛⊥｝←DSC（ω，SDKR，VEKS）．当S∈￠时，SC（m，SDKS，VEKR）＝Enc（m，VEKR），DSC（ω，SDKR，VEKS）＝ Dec（ε，SDKR）．

其中ENC＝ （Gen，Enc，Dec）为加密方案，Gen同上，ε←Enc（m，VEKR），m←Dec（ε，SDKR），SIG＝（Gen，Sig，Ver）为签名方案，Gen同上，τ←Sig（m，SDKS），｛T，⊥｝←Ver（τ，VEKS），T 表示签名有效，⊥表示无效．

3 新的广义签密方案

3．1 算法描述

（1）域参数

①密钥参数

本文用A表示发送方Alice，也即用户U，用ID表示Alice的身份，可信中心对Alice进行物理鉴定以确定ID具有唯一性；用B表示接收方Bob．令IG是RSA模数生成器，输入1k，在k的多项式时间输出1024bits的模N＝pq．其中p和q是512bits的随机奇素数．g是群Z＊N中阶为素数r的生成元，其中r是下限长度为160bits的元素；可信中心随机选择x∈RZ＊N，计算y＝gxmodN．公开｛N，g，y｝，保密｛x，r｝．

设 （N，e，d，G，H，k0，k1）←RGen（1k），（N，e）是RSA公钥，在这里为了避免文献［12］中e＝3时的微弱攻击，取e的值为5，d＝e－1（modφ（N））是RSA私钥，并且｜N｜＝k＝n＋k0＋k1，2－k0和2－k1为可忽略的量；n是明文消息的长度，且要求k0≤（log2N）／e，k0＝160（保证2－k0可以忽略）．

②会话钥的生成

可信中心首先计算QID＝G（ID），然后计算签密会话密钥是K．可信中心通过安全信道将签密会话密钥K分别发送给A和B．并公开｛N，g，y，ID｝．

③Hash函数：

G、H是两个杂凑函数，且满足：

（2）签密算法：

签密者Alice执行签密操作．注意下面的A就是Alice．B就是Bob．

注意：这里规定符号i0＝0，（i为任意的字符串），和数学上的定义不同．

m∈｛0，1｝n时，A执行：首先A对接收到的K进行验证其正确性．A验证等式（gy×y×gG（ID））K≡gmod N是否成立，成立说明接收的加密密钥是正确的．注意：上面定义中的B的密钥正是这里的K．

Else s←（s′‖w）dA（mod N），加入时间标志：设t为当前时间，计算T＝H（s，t）

5．用K对s进行加密，得到e＝EK（s）mod N

7．发送 （c，s，t）给接收方B

（3）解签密算法：

接收者B收到（c，s，t）后执行如下的解签密算法：

计算Δt＝tb－t，tb是接收者B收到签密文的时间，如果Δt大于规定的时间，则拒绝解密，否则进行如下处理：

1．接收者B对接收到的K验证其正确性，验证算法如下：

检验（gy×y×gG（ID））K≡gmod N是否成立．若等式成立，则会话密钥是有效的，否则无效．

3．用密钥K对e进行解密s＝Dk（e），因为e＝EK（s）；如果s＝φ，return⊥

否则，验证解密出来的s和接收到的s是否相同，并验证等式T＝H（s，t），是否成立，若成立，则进行如下步骤，否则拒绝；

4．验证签名：计算u＝（s）eA

5．分离u为s′‖w

7．如果H（l‖m‖K）＝w，return m，否则return⊥

3．2 公开验证

Alice如果否认她曾发出的签密文时，则由第三方来仲裁．Bob将解签密算法执行完时，公开s′和w，并连同l一起提交给可信第三方，同时可信第三方要求A把她的l也交给他．然后可信第三方执行下列验证算法．

首先对A提交的l和B提交的l比较是否相等，以防止欺诈行为．

4．验证H（l‖m‖K）是否与w相等，就可以验证签密是否属于Alice的操作．因为对签名s进行了加密，所以可以防止恶意攻击者截取修改签名，Alice就难以否认自己的签密行为；对s的加密操作还有另一层意义，是为签密操作和只有加密操作存在情况下的第6步操作做准备工作，这样可以增加m加密的随机均匀性．下面简化的签名操作也有同样的公开验证原理，这是此签密方案的优势之一．

Bao ＆Deng方案［13］是第一个可公开验证的方案，但它是基于一个非标准的签名算法，且公开了消息的哈希值H（m），不具有语义安全性．而新的签密方案的哈希值用K填充，并且不公开，所以不会影响机密性．

3．3 签名模式和加密模式在只需要保证消息完整性的环境中执行签名模式．令接收方R＝φ．签密方案将变成签名方案．

在只需要保证消息机密性的环境中执行加密模式．令发送方S＝φ，签密算法将变为一个加密算法．

3．4 广义签密的正确性

令S为Alice，R为Bob．

要证明签密方案的正确性，即证明DSC（SC（m，dA，QB），dB，QA）＝m ．

证明 等式左边为解签密算法：

把签密后的参数c，s，t，dB，QA代入上述解签密过程中，可得到DSC（（c，s，t），dB，QA＝m ∪ ｛⊥｝．因为s＝DK（e），计算T′＝H（s，t），是否有T′＝T，u＝ （s）eA，分离u为s′‖w，w‖l＝G（w）⊕s′，并验证等式H（l‖m‖K）＝w是否成立，即可验证签密的正确性．

（2）在签名模式下，R∈φ，dB＝0，QB＝0，算法将简化为签名算法．

签名者Alice执行签名操作：

SC（m，dA，0）

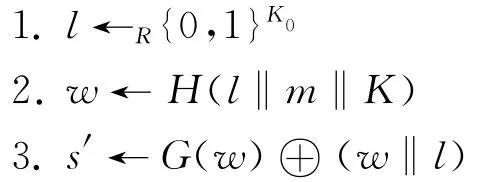
4．s← （s′‖w）dA（mod N），加入时间标志：设t为当前时间，计算T＝H（s，t）

5．用CFB模式的AES和密钥K＝0对m进行加密，得到密文0＝e＝E0（s）mod N

6．T‖m‖ ← （T‖m‖0）⊕0

7．Return Sig ＝ （m，s，t）

任一接收者执行验证操作：

DSC（Sig，0，QA）

1．K←0

3．把T分离出来，计算T′＝H（s，t），验证是否有T＝T′．如果等式成立，则说明s不是敌手重发的s

5．分离u为s′‖w

7．计算H（l‖m‖K）是否等于w，如果是，return m，否则return⊥；如果将空操作省去的话，即为签名方案，此签名方案的正确性是显而易见的．

（3）在加密模式下，S∈φ，dA＝0，QA＝0，算法将简化为一个加密算法．

任一加密者Alice执行加密操作：

SC（M，0，QB）

4．0＝s（s′‖w）0（mod N ），加入时间标志：t为当前时间，计算T ＝H（0，t）

5．用密钥K对m进行加密，得到密文e＝EK（0）

6．c＝ （T‖m‖0）⊕K

7．Return Sec＝ （c，t）

接收者Bob执行解密操作：

DSC（Sec，dB，0）

1．（T‖m‖0）＝c⊕K

2．从（T‖m‖0）中分离出T，计算T′＝H（0，t），验证t′是否等于T，如果相等return m，否则return⊥

4 新的广义签密方案的安全性

签密安全性的形式化证明主要是建立在加密和签名的可证明安全性理论基础之上，本文在此基础上对新的方案进行了安全性归约证明．

定义4 整数分解问题 （IF问题）

输入 N：奇合数，至少有两个素因子．

输出 奇素数p，q满足p｜N，q｜N．

只有在选择适当参数的条件下，IF问题才是困难的．

假设1 整数分解假设 （IF假设）一个整数分解器是一个PPT算法Α，满足概率ε＞0：

ε＝Prob［Α （N）整除N，1＜A （N）＜N］

其中Α输入由定义4确定．

令IG是整数生成器，输入1k，在k的多项式时间输出2k比特的模N＝pq．其中p和q是k比特的随机奇素数．

说IG满足整数分解 （IF问题），如果对于足够大的k，以不可忽略的概率ε＞0，不存在由IG （1k）所产生的整数分解算法．显然，一个能解IF问题的算法就能解RSA问题．也就是说解RSA问题就等价于解数学难题IF问题．

假设2 （Random Oracle假设） Hash函数H和G具有Random Oracle（随机预言机）属性，即Hash函数是确定的、有效的、不可逆的输出服从均匀分布的函数．

4．1 加密密钥的可验证性

当发送方和接收方收到从秘密信道传送过来的密钥K时，通过等式（gy×y×gG（ID））K≡gmod N验证K的正确性，有效防止密钥K的修改伪造和中间人攻击．因为密钥是由可信第三方产生的，所以密钥K的可信度高．

4．2 不可伪造性

假设签密的伪造者为Bob和Malice，因为Bob拥有解签密时用到的私钥dB，也即K，因此Bob伪造的能力最强．Bob对Alice发送来的签密利用可公开验证密钥K对其进行解签密，得到签名，于是对签密的伪造就转化为对签名的伪造．假设Bob有伪造的能力，此时Bob已经解签密得到了签名，并且已经验证了签名的正确性，Bob进行下面的运算，

1．验证签名：计算u＝（s）eA

4．如果H（l‖m‖K）＝w，return m，否则return⊥

尽管如此，因为Bob不知道Alice的私钥dA，所以Bob无法进行签名伪造．又由定义4和假设1可知Bob要想通过分解N求得签名的任何消息是不可能的，因为Bob不知道N的分解．又因为签名是串s′和w的连接，不满足中间相遇攻击的条件，所以可以抵抗中间相遇攻击．只要Bob不能伪造签密，Malice就更不可能伪造签密．因为Malice拥有的条件比Bob更少，伪造的能力就更弱，所以该签密方案是不可伪造的．

4．3 不可否认性

签密的不可否认性等价于签密的不可伪造性，如果不存在副本签密［14］，则不可伪造性蕴含不可否认性．假如可能伪造签密，则Alice就有机会否认，因为Bob和可信第三方没有足够的证据证明签密来自Alice．因为该方案中的函数映射都是一一对应，不出现二维映射，即不出现两个不同的横坐标同时映射到纵轴上同一坐标的情况，所以不出现副本签密的情况．又因为在签密的过程中加入了时戳的使用，且T是加密的，具有安全性质，所以可以防止签名s的重放攻击．

该方案的不可伪造性可通过上述的可信第三方公开验证的方法来实现，因此该方案满足不可否认性的要求．

4．4 机密性

定义5 （单向性） 函数f在（t，ε）域上是单向的，如果任意一个攻击者A在时间不超过t内恢复

f（s‖w）的原像的成功概率的上界是ε，那么就说该函数f是具有单向性的．可以用下面的式子表示：

定理1 新的广义签密方案是IND－CCA2可证明安全的．

证明 套用文献［15］的引理和推论证明该定理．

前提条件：假设该签密方案中的RSA函数满足定义5的单向性．

引理 在这里用A表示一个利用CCA2攻击该新的广义签密的攻击者，假设A执行时间t后以优势ε至多分别向签密预言机和解签密预言机作了qg，qh，qs和qu次询问．用f表示k比特的门限，用f′表示单向置换f的归约置换．那么有下面的式子：

其中t′＝tg·（qg＋qh＋qs）＋th·（qh＋qs）＋ts·qs＋tu·qu，tg是用来模拟随机预言机G所花费的时间，th，ts的定义类似．

推论 用引理中的符号有：

证明 要证明攻击者A是怎样通过计算c＊的部分原像来攻破单向函数f′的，A并不知道求f的原像的任何秘密信息．

现在假设目标发送者Alice知道怎样求f的值，目标接收者Bob知道怎样求f－1的值，用所有公开参数和Alice及Bob的公钥运行A，在这里有必要证明A怎样对随机预言机G和H、签密预言机和解签密预言机所作的询问进行反应．分别用符号Gsim、Hsim、Ssim、Usim表示这些模拟算法．下面将具体描述．

要使得模拟真实，需要分别保存两张表LG和LH，它们初始化为空，表LG由对随机预言机G进行提问的询问／应答对组成，表LH由对随机预言机H进行提问的询问／应答对组成．在模拟的结束，希望找到在LG询问期间得到的c＊的部分原像．

注意到：在Hsim中，假设每一次的询问都有形式l‖m‖K，这意味着每次的询问都有k0＋n＋＊比特长，这里的＊的值根据K的长度确定．其中m有n比特，l有k0比特，K有＊比特，之所以作这样的假设是因为在随机预言机模型中，它不会帮助A做出任何长度等于k0＋n＋＊的不同的询问．也允许A向Ssim做形如l‖m‖K的询问．

在查找阶段的结束时，A输出m0和m1，模拟器随机选择一个比特b和K＊，给攻击者A提供mb的签名s＊，假设s＊＝f（s′＊‖w＊），对随机预言机G和H 有：

用AskG表示A在LGH‖‖的事件．

如果w＊∉LG，那么G（w＊）未定义，l＊是随机均匀分布的变量，有可能存在这样一个M，使得l＊‖m‖K＊∈LH的概率至多为2－k0＋＊·（qh＋qs）．由此得出：

当一个密文有效时，如果输出拒绝，模拟器Usim可能仅仅是失败，这里用UBad表示该事件．假设Usim以s＝f（s′‖w）的形式被询问，且让w‖l＝G（w）⊕s′成立．当l‖m‖K 不在LH中时，如果H（l‖m‖K）＝w，或许会错误地拒绝一个有效的密文．假设询问发生在s＊被发送给A之前，由于l‖m‖K不在LH中，H（l‖m‖K）将随机地取值．如果询问发生在S＊被发送给A之后，那么s≠s＊意味着（m，l，K）≠ （mb，l＊，K＊）．在这两种情况下H（l‖m‖K）随机取值意味着

定义事件

如果攻击者取得成功，则它输出b，且b′＝b，用S表示这一事件．在事件⇁Bad，比特b独立于模拟器，也独立于攻击者，由此得出：

在事件⇁Bad中，攻击者和一个随机预言机、签密预言机和解签密预言机的完美仿真进行交互，由此得出：

从公式 （5）可以得到：

由公式 （6）（7）可以得出：

从 （4）得到：Pr［Bad］≤Pr［AskG ∨AskH］＋Pr［UBad］

由公式 （2）（3）（9）我们得到：

从上面的证明看出该证明结果中2－（k0＋＊）·（qh＋qs）的值比文献［10］中在证明抽象 TBOS的IND－CCA2安全时推得的结果中2－k0·（qh＋qs）的值小，所以如果文献［10］中的pr［AskG］可以忽略，则该证明结果中的pr［AskG］同样可以忽略．并且可以忽略的程度根据K的长度决定，K的长度越长，可以忽略的程度越高，否则相反．由此得出该新的广义签密方案中的签名部分是IND－CCA2可证明安全的．因为m在签名前是用假设2中的安全哈希函数处理过的，且处理的过程中加入了随机化比特串和密钥种子，由此得到的哈希值的随机均匀性好，所以攻击者是无法通过求哈希函数的逆达到攻击的目的．因此即使该方案中的签名信息是公开传给Bob的，如果在不知道明文消息m（除了Bob）的情况下是很难伪造的．又因为m在加密的过程中是用签名s加密后的随机串填充后进行的，加密后的密文是随机均匀分布的，所以攻击者不可能通过猜测密文的方式得到m．经过上述分析，该新的广义签密方案的安全性等同于OAEP的安全性［16］．

4．5 消息认证的性质

定理2 该新的广义签密方案具有消息认证的性质．

证明 很明显，该新的广义签密方案具备了文献［9］中定义的消息认证的条件，因此该新的方案具有消息认证的性质．

所以经过以上证明分析，该方案具备了定义2所具有的安全性质．

5 效率分析

5．1 计算复杂性分析

该新的签密方案的签名部分是基于RSA签名的，加密部分是基于对称加密算法的，它的算法简单，效率高．在公钥密码体制中，有限域上的模乘、模幂、（指数）、模逆计算复杂度较高．相比之下，有限域上的加法、hash、对称加／解密，所消耗的时间可以忽略．下面的表给出了该方案和其他几种签密体制的效率比较．

表1 计算量比较表格

5．2 与基于离散对数的方案的比较

SCS是表1中基于离散对数的方案中最快的一种．根据文献 ［11］中的数据，同等安全条件下椭圆曲线上的点的标量乘大约是模幂运算量的1／8，根据此结果，SC－ECDSA密钥生成的运算量约为SCS的1／8；SC－ECDSA签密操作的运算量约为SCS的1／4；解签密的运算量约为SCS的1／5．而本方案的密钥生成的运算量以及签密操作的运算量大致和SCS相等；而解签密操作的运算量为SCS操作的1／2；同时本方案比SCS方案优越的一个方面是该方案增加了公开验证操作．该方案的优势和TBOS相比是明显的．但比起SC－ECDSA方案运算量稍微大些，这是椭圆曲线本身固有的性质，可是它只适用于小型系统．而新的广义签密方案适用于大小系统，可以弥补SC－ECDSA方案的不足．

6 结 语

在已有的广义签密的基础上提出了一种新的可公开验证的广义签密方案，该新的方案不但可以适用于签名加密单独存在的场合，而且密钥K具有可公开验证的性质．密钥K的长度下限短，适用于签密长度不受限制的场合，且新的方案是IND－CCA2可证明安全的．经过效率分析，它的计算量大小适中，使用场合弥补了SC－ECDSA方案的不足，是一种有效的广义签密方案．但该新的广义签密方案的计算效率还不够好，需做进一步的研究．

［1］ Zheng Y．Digital signcryption or how to achieve cost（signature＆encryption）＋cost（signature）＋cost（encryption）［A］．Kaliski BS．Proceedings of CRYPTO’97 ［C］．Berlin：Springer－Verlag，1997：165－179

［2］ Nalla D，Reddy KC．Signcryption scheme for identity－based cryptosystems ［EB／OL］．http：／／wenku．baidu．com／view／60fcf68a84868762caaed58dHhtml．

［3］ Hwang RJ，Lai CH，Su FF．An efficient signcryption scheme with forward secrecy based on elliptic curve［J］．Appl Math Comput，2005，16 （07）：870－881

［4］ 张串绒，肖国镇．一个可公开验证签密方案的密码分析和改进 ［J］．电子学报，2006，34（01）：177－179

［5］ Tan CH．Analysis of improveed signcryption scheme with key privacy ［J］，Inform Proc Lett，2006，99 （04）135－138

［6］ 彭长根，李祥，罗文．一种面向群组通信的通用门限签密方案 ［J］．电子学报，2007，35（01）：4－67

［7］ 邱红丽，曹珍富．基于强RSA假定的前向安全签名方案 ［J］．计算机工程，2005，31（09）：64－66

［8］ Mao WB．Modern Cryptography：Theory and Practice［M］．北京：电子工业出版社，2004，7

［9］ Lee JM，Mao W．Two birds one stone：signcryption using RSA ［A］．Okamoto T．Proceedings of the RSA Conference 2003 ［C］．Berlin：Springer－Verlag，2003：210－224

［10］ Han YL，Yang XY．ECDSA可公开验证广义签密方案 ［J］．计算机学报，2006，29 （11）：2003－2011

［11］ Daniel R，Brown L．A weak－randomizer attack on RSA－OAEP with e＝3 ［EB／OL］．http：／／wenku．baidu．com／view／ab00e235f111f18583d05ab9．html．

［12］ Bao F，Deng RH．A signcryption schemes with signature directly verifiable by public key ［A］．Krawczyk H．Proceedings of the Public Key Crypto’98 ［C］．Berlin：Springer－Verlag，1998，55－59

［13］ Stern J，Pointcheval D，Lee JM，et al．Flaws in applying proof methodologies to signature schemes［A］．Motied Y．Advances in Cryptology－Crypto’02 ［C］．Berlin：Springer－Verlag，2002，93－110

［14］ Coron JS，Joye M，Naccache D．Universal Padding Schemes for RSA ［A］．Motied Y．In Advances in Cryptology－CRYPTO 2002 ［C］．Berlin：Springer－Verlag，2002：226－241

［15］ Shoup V．OAEP Reconsidered ［EB／OL］．http：／／wenku．baidu．com／view／8bec8f0690c69ec3d5bb7551．html．

［16］ Koblitz N，Menezes A，Vanstone D．The states of elliptic curve cryptography［J］．Designs Codes Cryptogr，2000，30（19）：173－193

New RSA－TBOS Generalized Signcryption Scheme

WANG Hui－ge，CAO Hao，LIU Bin，ZHUANG Suo－fa，SHEN Feng
（College of Science，Anhui Science and Technology University，Fengyan 233100，Anhui，China）

To resist adaptive chosen ciphertext attack，improve efficiency of the signcryption generation and strengthen the possibility to share secret，apublicly verifiable generalized signcryption scheme is put forword．Compared with Han Yi－liang’s our scheme ismainly based on the difficulty of the decomposition of RSA biginteger，and the length of the secret key in the scheme is not more than 160bites and it can realize short signcryption．The computational complexity of our scheme is between that of Han yi－liang’s and Malone－Lee’s．Because the signature in the new scheme is the linkage of two information after padding at random，it can resist the middle meeting attack．Finally，parts of IND－CCA2security of the new seheme is proved．

signcryption；generalized signcryption；digital signature；public verifiable

TP 309

A

1673－1492 （2011）06－0020－09

来稿日期：2011－10－10

安徽省教育厅自然科学项目 （KJ2010B059）；安徽科技学院安徽省自然科学基金预研项目 （ZRC2011274）

王会歌（1981－），女，河南许昌人，安徽科技学院理学院教师，硕士．

刘守义 英文编辑：刘彦哲］