Frobenius范数‖·‖Σ下的逆收敛速度

吴建春

（酒泉职业技术学院，甘肃酒泉735000）

0 引言

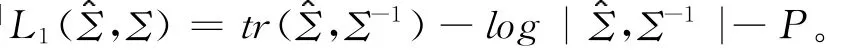
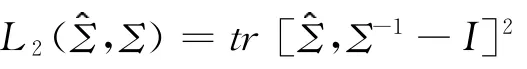
1 引理［2］

设bn＝E‖y‖2，cn＝max1≤i≤kE）且dn＝max1≤i≤kE）。

引理1 （f1，y1），…，（fn，yn）是（f，y）的ni.i.d样本。E（ε｜f）＝0 cov（ε｜f）＝Σn，0是对角线。而且分布是连续的，且K≤p。

引理2 bn＝O（p）且序列cn和dn是有界的。同时也存在一个常数σ1＞0，使得对所有的n来说都有λk（cov（f））≥σ1。

引理3 存在一个常数σ2＞0，使得对所有的n来说都有λp（Σn，0）≥σ2。

2 定理

定理 在引理1—3下，我们得出

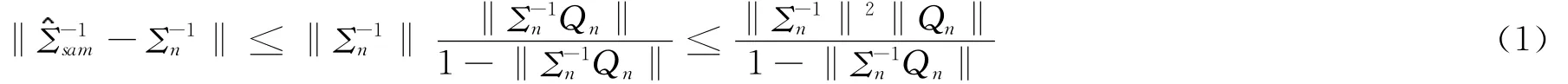
显而易见‖Qn‖＝Op（n－1／2pK），得出‖‖＝O（p－1／2），因为pK1／2＝o（（n／logn）1／4），可以得到和

接下来，来证明Σ－1在范数下的弱收敛性。基本设想是验证Σ－1的各个项的估计错误。

这与Sherman－Morrison－Woodbury公式一起说明了

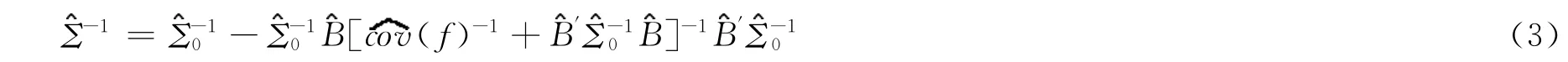
因此，我们可得出

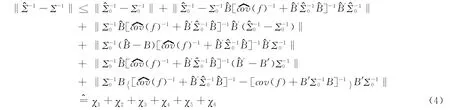
从引理3中可了解到，Σ0的对角线被限定为远离0。注意和Σ0都是成对角线的，因为pK1／2＝0（（n／logn）1／2），我们就能很容易地证明

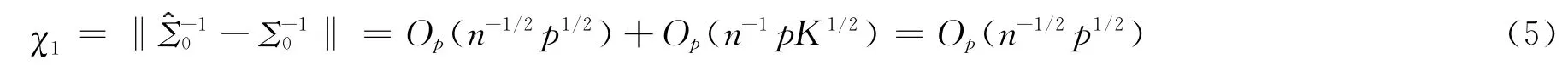
现在我们来考虑第二个项χ2。

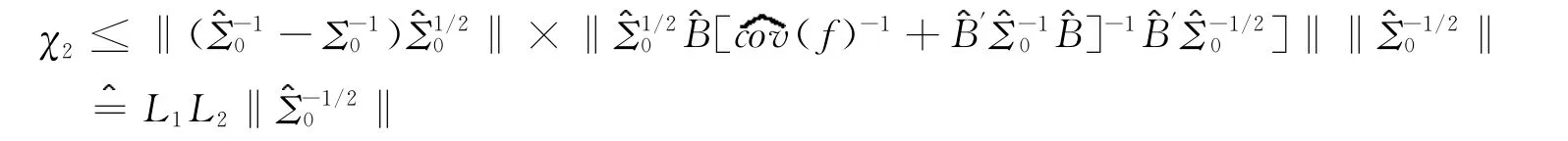
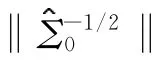
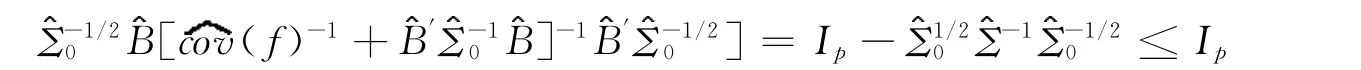
同样地，我们可以证明

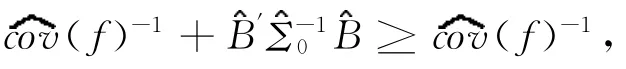
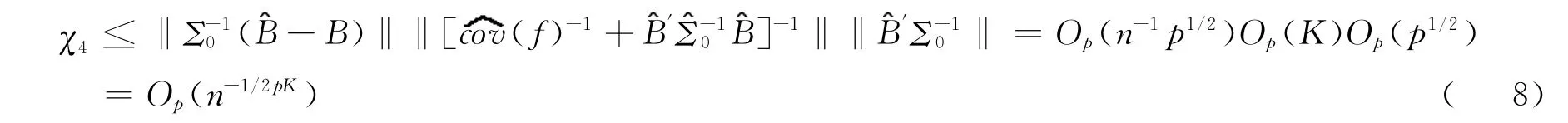
和

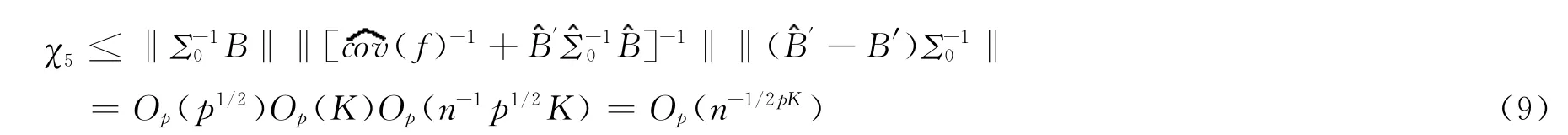
最后，利用定理3的证明的上半部分中的论点，我们可以证明［6］

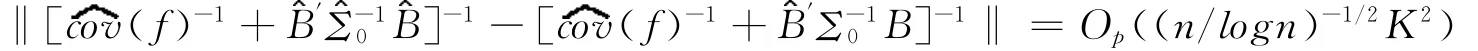
由此，我们得出

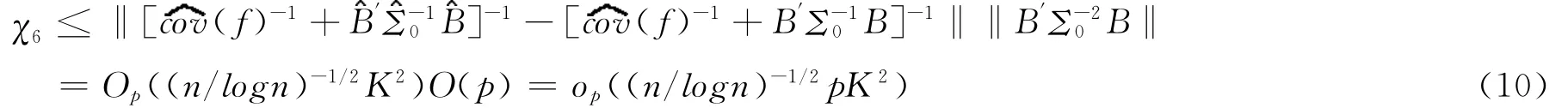
［1］苏化明，黄有度.一类数列极限的收敛速度［J］.高等数学研究，2004（7）：20－22.

［2］林 祥.不变分布及收敛速度［D］.中南大学，2003（1）：43－44.

［3］李杰红，赵华敏.关于矩阵方程AX＋YB＝C反问题的极小Frobenius范数对称解［J］.天津科技大学学报，2006（3）：63－65，69.

［4］马景义.析主成分分析和因子分析——以Frobenius范数下矩阵近似的新视角［J］.统计教育，2010（5）：43，54－56.

［5］张 静.行NA组列加权和的完全收敛速度［C］／／中国数学力学物理学高新技术交叉研究学会第十二届学术年会论文集，2008：516－517.

［6］邹黎敏，姜友谊，胡兴凯.关于矩阵Frobenius范数的一个猜想［J］.山东大学学报（理学版），2010（4）：48－50.