基于自回归模型的上海港港口吞吐量的预测

徐志刚

(上海海事大学，上海 200135)

0 引言

经济预测是指在有关的宏、微观经济学理论指导下，以经济发展的历史和现状为出发点，以调查研究和统计资料为依据，以科学的定性分析和严谨定理计算为手段，对预测对象有关经济活动的发展演变规律通过预测模型进行分析和解释，从而对预测对象的未来发展演变程度预先做出科学的推测。可是未来的变化会受到各种复杂因素的影响，充满着不确定性，预测的目的就是力求对未来经济发展过程中的不确定性达到极小化。

现代经济学中的预测方法很多，定性预测的方法主要有德尔菲法、小组意见法、专家评估法等，这些方法所得到的信息大多是非量化的、主观的，与当前的预测相关程度低，适合于中期到长期的预测研究。定量预测的方法很多，如适合用于短期预测的时间序列平滑预测法、神经网络法等，适合用于中、长期预测的动态模拟法、自适应滤波预测法、灰色预测法等。可是预测方法和模型的简单与复杂程度并不决定预测结果的关联程度，简单的预测方法也能够较清晰的得出预测结果。

1 自回归预测法

回归分析是关于研究一个叫做因变量的变量对另一个或多个叫做解释变量的变量的依赖关系，其用意在于通过后者的已知或设定值，去估计和预测前者(总体)的均值。

自回归预测法是指利用预测目标的历史时间数列在不同时期取值之间存在的依存关系(即自身相关)，建立起回归方程进行预测。具体说，就是用一个变量的时间数列作为因变量数列，用同一变量向过去推移若干期的时间数列作自变量数列，分析一个因变量数列和另一个或多个自变量数列之间的相关关系，建立回归方程进行预测。

自回归预测法的优点是所需资料不多，可用自变量数列来进行预测。但是这种方法受到一定的限制，即必须具有自相关。这种方法只能适用于某些具有时间序列相关趋势的经济现象，即受历史因素影响较大的经济现象，如各种开采量，各种自然产量等。对于受社会因素影响较大的经济现象，不宜采用这种方法。

1.1 自回归预测法的步骤

第一步，确定自相关数列。根据预测目的和要求，对预测目标的时间数列资料(月、季、年度)加以整理，使之具有可比性，并将这些数列划分为因变量和自变量数列。因变量数列的期限(即项数)，可以根据时间数列所反映周期变动规律确定。自变量数列，可用原时间数列向后逐期推移取得，它的期数必须同因变量数列相同。

第二步，确定回归模型。计算各个自变量数列的自相关系数，自相关系数的计算方法同一般相关系数的计算方法相同。根据自相关系数的大小，确定自变量，即选择自相关系数较大的自变量数列，用以拟合回归模型。自回归模型可以是线性的，也可以是非线性的;如果自回归模型中只有一个自变量，称为一阶(一元)自回归模型;有两个自变量，称为二阶(二元)自回归模型。在做相关经济预测中，一般用向后推移一期或两期的一阶(元)线性自身回归。因为二阶(元)以上的自身回归计算复杂，并不能提高预测准确度，用处不大。

第三步，估计参数，利用模型预测。模型参数值的求法，与其它回归模型的参数求法一样。预测期的自变量，就是自变量数列的下一期数值，在原时间数列中可以找到，用于进行预测。对预测值的可靠性检验，数列中可以找到，用于进行预测。对预测值的可靠性检验，也与其它回归模型相同。

2 上海港货物吞吐量的预测

2.1 模型创建思路

首先，因为所收集的上海港货物吞吐量是月度数据，所以考虑到可能会存在季节(月度)效应，从而设置了月度虚拟变量D2，D3……D12。把1月份设为基准类，那么，D2=1表示2月份，D3=1表示3月份，以此类推，D12=1表示12月份。当D2=D3……D12=0时，则表示1月份。

其次，由于货物吞吐量数据是时间序列数据，而不同月份的货物吞吐量之间可能存在前后相依的关系，故考虑采用自回归模型，即把Zt的滞后项作为模型的解释变量，但到底要引入几阶滞后项，才能最大限度的消除数据之间的自相关性，需要进行多次的尝试，方法是先引入一阶滞后项Zt－1，然后根据数据结果检验，再引入二阶滞后项，再检验，以此类推，直到满足检验条件为止。即当Durbin－Watson值最接近2时所得到的模型即为本次预测的最佳模型。

2.2 变量的引进及数据来源

根据预测的需要，引进因变量:Zt、Yt，月度虚拟变量 D2，D3……D12。其中:C1表示常数，C2，C3…… C15表示变量系数，Zt代表上海港货物吞吐量，Yt代表上海港集装箱吞吐量。表1、表2中的数据分别为上海港货物吞吐量的月度数据(2001年1月至2010年6月)和上海港集装箱吞吐量的月度数据(2001年1月至2010年6月)。

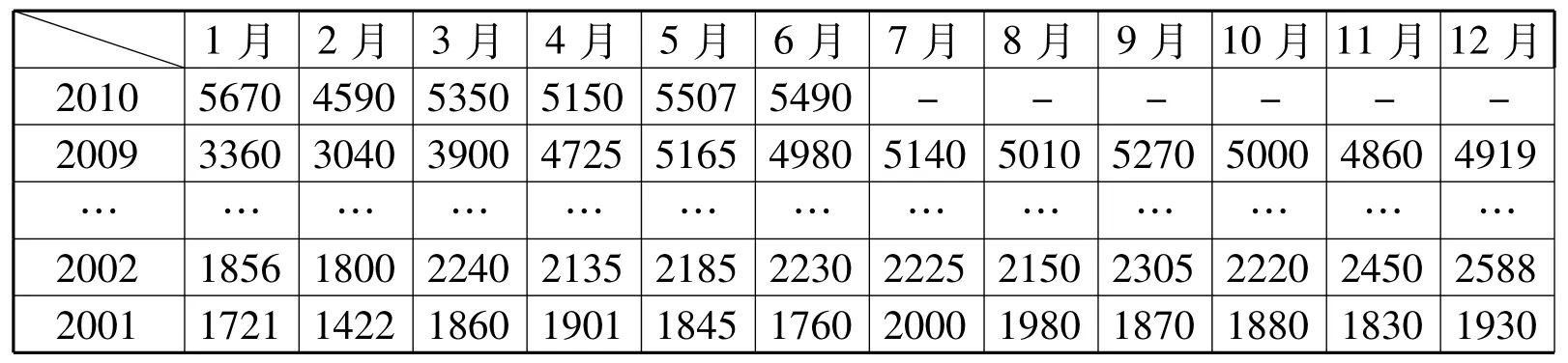
表1 上海港货物吞吐量(单位:万吨)

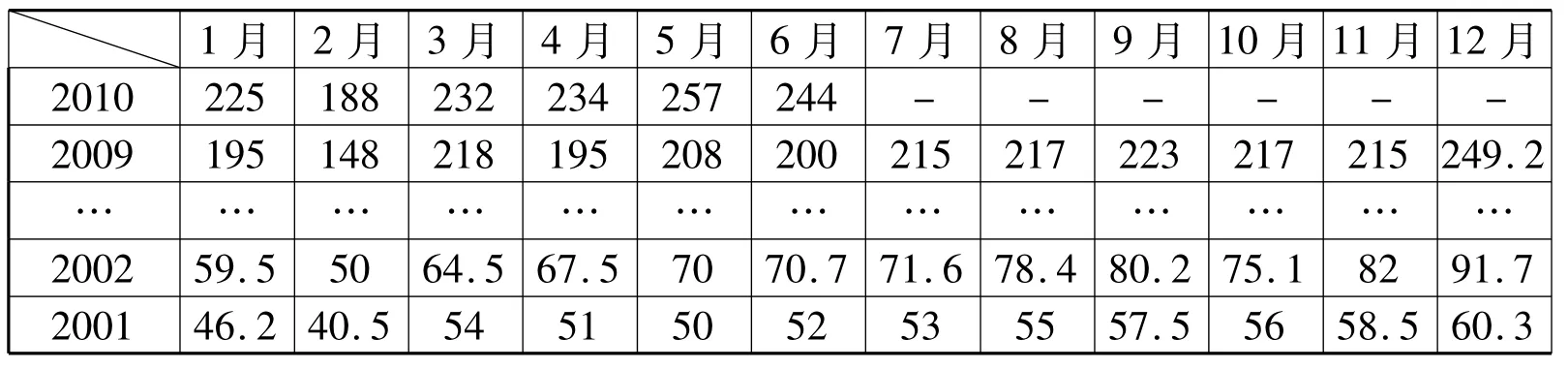
表2 上海港集装箱吞吐量(单位:万TEU)

2.3 模型创建过程

2.3.1 先建立初始模型

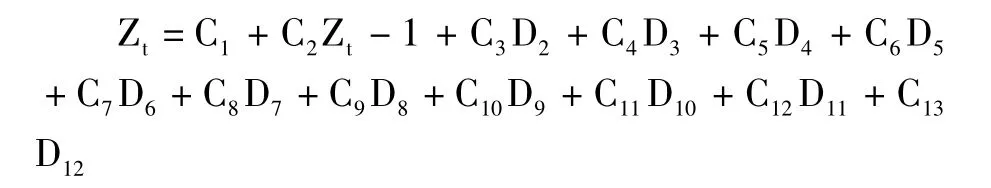
用views5.0软件处理数据，并对部分数据分析如下:

(1)滞后项 Zt－1对应的 P 值小于 0.0001，因而该变量是显著的，引入它是有必要的。

(2)多数月度虚拟变量对应的P值也很小(多数小于0.1或0.05)，因而月度季节效应也较为明显。

(3)R －squared(拟合优度)的值为 0.942781，说明模型的解释能力比较高。

(4)Prob(F－statistic)的值相当小(小于0.0001)，意味着该模型在总体上是显著的。

(5)Durbin－Watson 的值为 2.747816，不是很接近2，因而该模型还存在一定程度的自相关性。

结论:必须对其进行修正。改进方法:增加二阶滞后项 Zt－2。目的是消除自相关性。

2.3.2 第二次创建的模型

第二次创建的模型(增加了二阶滞后项Zt－2)如下:

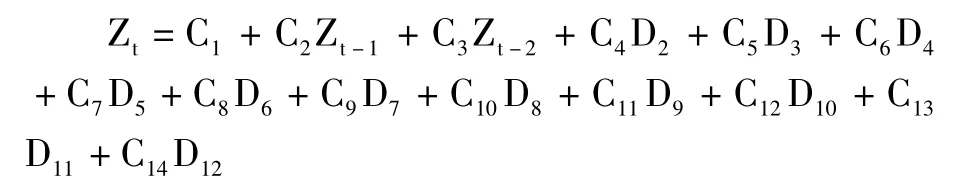
用views5.0软件处理数据，并对部分数据分析如下:

(1)滞后项 Zt－1和 Zt－2对应的 P 值都小于 0.0001，说明变量仍然很显著，因而引入这两个滞后项都是有必要的。

(2)多数月度虚拟变量对应的P值也很小(多数小于0.1或0.05)，因而月度季节效应也较为明显。

(3)R －squared(拟合优度)的值为 0.949586，说明模型的解释能力比较高。

(4)F值对应的P值相当小(小于0.0001)，意味着该模型在总体上是显著的。

(5)Durbin－Watson的值为 1.958747，已经很接近于2，因而可以近似认为模型不存在自相关性问题了，所以，无须对其进行修正。

但是，为了更加准确的说明自相关问题不存在，也可以再次引入三阶滞后项 ，然后对其做变量显著性检验，以考察是否有引入的必要。同理建立模型作相应分析，从而得出结论:Zt－3所对应的P值为0.6238，远大于通常的显著性水平 0.1、0.05 和0.01，可见引入三阶滞后项没有必要。

2.3.3 结论与预测结果

根据上面三个模型的估计结果及其检验分析，可以看出，在现有条件下第二个模型是最优的模型，因此，可以采用第二个模型的估计结果来对Zt变量未来的取值进行预测或估计。对第二个模型的变量系数进行赋值，即:

利用Eviews5.0的预测功能，得到如下数据结果(见表3)(取小数点后2位)并得出相应的曲线，如图1所示。

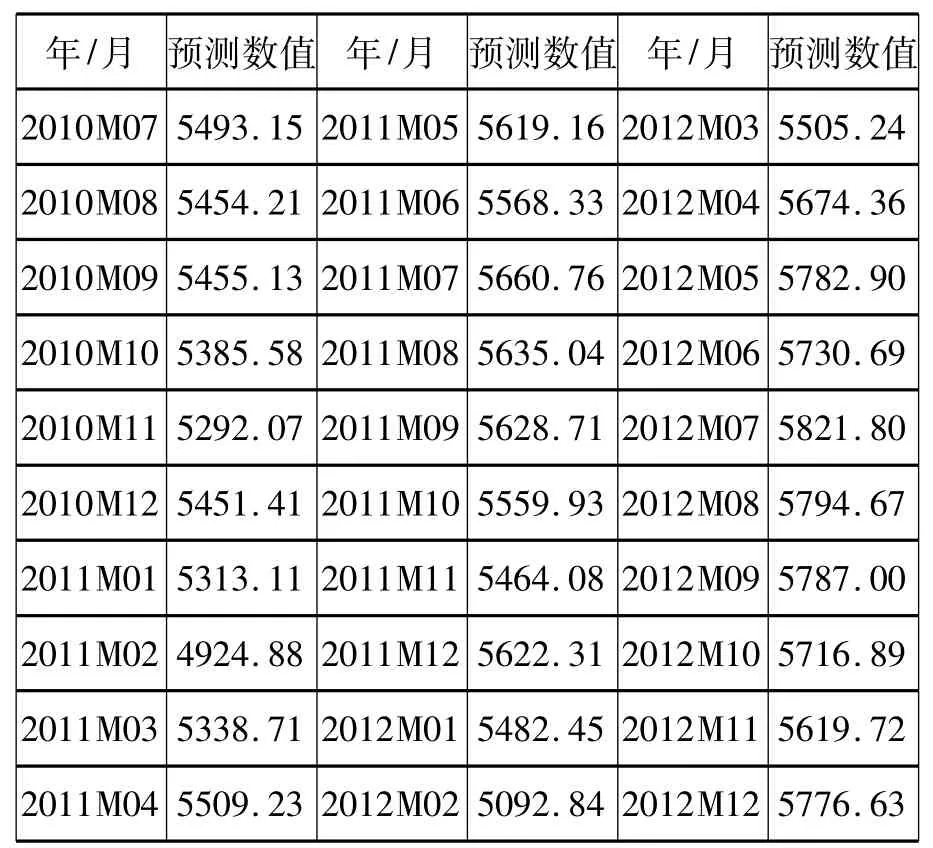
表3 上海港货物吞吐量预测值(单位/万吨)

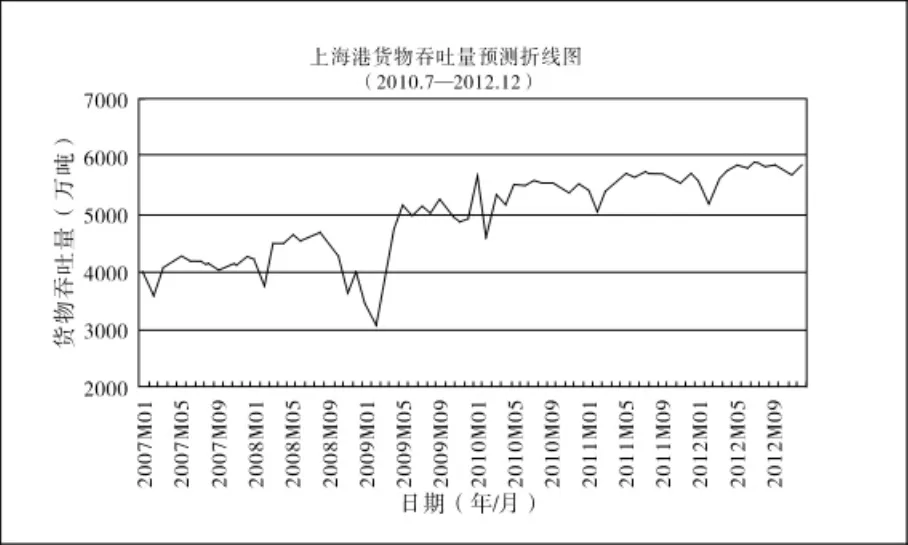
图1 上海港货物吞吐量折线图

2.4 上海港集装箱吞吐量的预测

按照上述建模的思路和方法，同样的依次增加Yt的滞后项来尝试创建更加准确的模型，从表中可以看出，当引入三阶滞后项时，此时滞后项 Yt－1、Yt－2和 Yt－3对应的 P值都很小，多数月度虚拟变量对应的P值也很小(多数小于0.1或0.05)，R－squared为0.980805，F值对应的P值相当小(小于0.0001)，意味着该模型在总体上是显著的。最后，Durbin－Watson值为2.017566，已经很接近于 2，因而可以近似认为模型不存在自相关问题了，所以，无须对其进一步修正，此模型为最优模型。即:

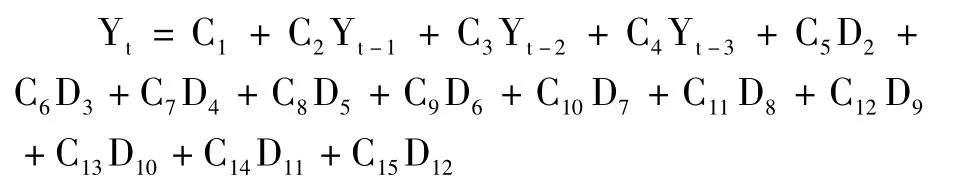
所对应的模型估计结果如下:

利用Eviews5.0的预测功能，得到数据结果如表4所示(取小数点后2位)，并做出相应的曲线，如图2所示。

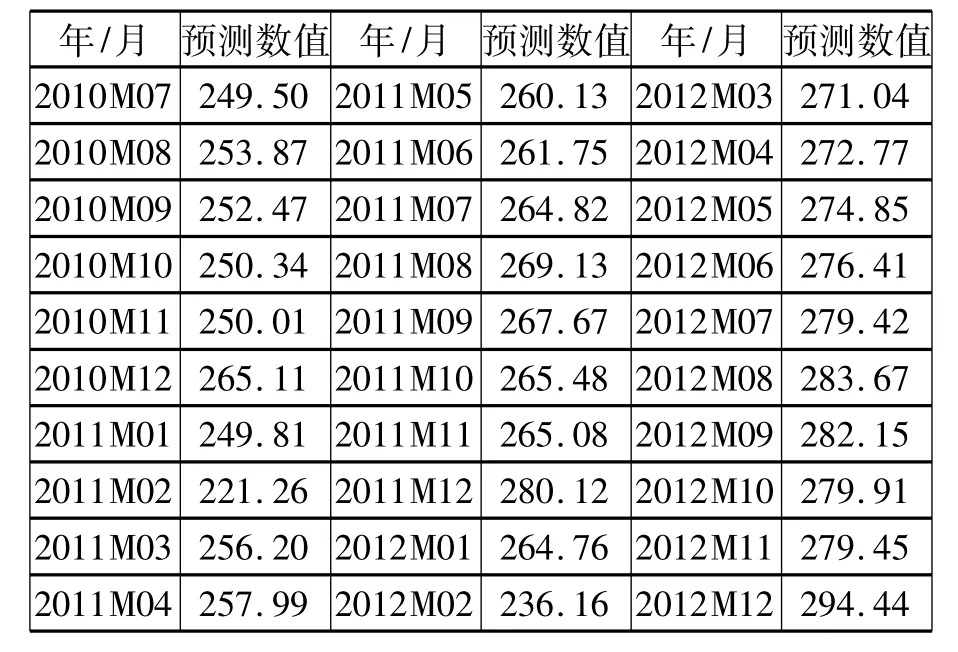
表4 上海港集装箱吞吐量预测值(单位/万TEU)

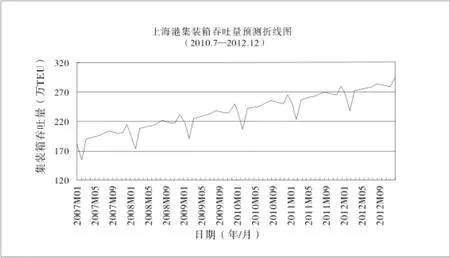
图2 上海港货物吞吐量折线图

3 小结与建议

从图1、2中的折线图可以看出，吞吐量在保持整体上升趋势的同时，在不同的年份存在相同的季节性差异，尤其是集装箱吞吐量的折线图表现的极为明显，在每年第一季度都出现了不同程度的下降。

通过计算，自2001年－2012年上海港货物吞吐量和集装箱吞吐量分别以平均10.22%和16.93%的年增长速度递增(数据计算中包括2010年6月至2012年2月的预测数据)，按预测结果到2012年底，全年货物吞吐量和集装箱吞吐量将分别达到68000万吨和3300万TEU。

可以设想到2015、2020年甚至更远的年代，作为集疏运体系中负荷量最大的公路运输肯定不能满足运输量的要求。作为运输量大、耗能低、污染少的内河运输方式应该成为集疏运体系中的一个重要组成部分，当然内河运输同时存在耗时、滞港等不利因素。为了运输发展的需要，同时也是配合上海国际航运中心建设的战略需要，上海内河运输的发展应被充分的研究和规划。只有不断建设发展公路、铁路、内河等联运条件，才能逐步形成较为完善的上海港口集疏运体系。

［1］达摩达尔·N·古扎拉蒂.计量经济学基础(第四版)［M］.北京:中国人民大学出版社，2005.

［2］樊欢欢，张凌云.Eviews统计分析与应用［M］.北京:机械工业出版社，2010.