水性质的分子动力学模拟研究

吴方棣 郑辉东 吴燕翔

(1.武夷学院 环境与建筑工程系，福建 武夷山 354300；2.福州大学 化学化工学院，福建 福州 350108)

水性质的分子动力学模拟研究

吴方棣1郑辉东2吴燕翔2

(1.武夷学院 环境与建筑工程系，福建 武夷山 354300；2.福州大学 化学化工学院，福建 福州 350108)

本文采用SPC/E水模型对水的性质进行了分子动力学模拟研究。结果表明，与常态及亚临界状态下相比，超临界下水的密度随温度压力的变化更为显著，这是超临界水具有较高溶解能力的重要原因；且在超临界下其自扩散系数明显增大，表明在超临界下水有着更高的扩散能力。在常态下水分子主要形成了二至四个氢键的结构，占了70%以上；随着温度的升高，每个水分子平均形成的氢键数减少。水表面张力模拟值与实验值相比偏小,其原因是未考虑氢键等因素对表面张力的影响。

水；密度；扩散系数；氢键度；表面张力；分子动力学模拟

1 引言

分子动力学(Molecular Dynamic，简称MD)是研究在某一条件下分子体系的各种性质随时间变化，它是以特定粒子(如原子、分子等)为基本研究对象，将系统看作具有一定特征的粒子集合，运用经典力学和统计力学方法，通过研究微观分子的运动规律，得到体系的宏观特性和基本规律[1]。分子动力学模拟作为一种理想的计算机实验方法，随着计算机技术的发展，近年来其广泛应用于化学化工、生命科学、医学、力学及材料科学等各个领域。

物质物性数据的获得通常有实验测定、模型计算以及近年来迅速发展起来的计算机模拟等方法。分子动力学模拟不仅可以获得物质的平衡性质，还可以获得物质的传递性质如：扩散系数等。水是我们日常生活中不可缺少的物质，它在化工生产过程中被广泛用作溶剂、冷却剂、萃取剂等。因此近年来广大学者对其性质也进行了较为深入的研究。本文采用分子动力学模拟方法，对不同条件（从常态至超临界状态）下水的密度、自扩散系数、氢键数以及表面张力做了较为全面的模拟研究。

2 模拟方法

2.1 势能模型选择

现常用的水的势能模型有SPC、SPC/E、TIP4P等，其分子结构及势能参数如表1，其中A、B为LJ参数。

表1 水模型参数表Table 1 The parameters of differentwatermodel

为了选择更为适合的水模型，我们分别计算了25℃、1atm下这三种模型的密度和扩散系数，结果如表2所示。

表2 在25℃、1 atm下不同水模型的密度及扩散系数的模拟值Table 2 The simulative density and diffusion coefficient of different water model at 25℃,1 atm

从表2可以看出，TIP4P计算的密度与实验值最接近，但扩散系数相差较大，而SPC/E的密度与扩散系数都与实验值的误差很小，因此SPC/E水模型能够提供更为准确的数据，从而本文采用SPC/E水模型进行计算。

2.2 模拟细节

本次的分子动力学 (MD)模拟采用的是GROMACS4.0.5[4]软件包。模拟采用NPT系综，三维周期边界条件，压力耦联采用berendsen[5]方法，温度耦联采用v-rescale[6]方法。采用PME[7,8]算法进行静电相互作用力计算，库仑截断半径为10 A°。范德华截断半径为12A°。对所有键长采用LINCS[9]进行抑制。模拟的时间步长为2 fs，每隔1 ps保存一次坐标数据，为保证体系达到平衡，每个计算体系模拟时长为4-6 ns。

3 结果与讨论

本文模拟过程水分子数为4176个，下面分别对水的密度，自扩散系数，氢键度以及表面张力进行研究分析。

3.1 水密度的计算

采用NPT系综计算了不同温度、压力下水的密度，并与文献值进行了比较，结果如表3所示。表3中常态及亚临界状态密度文献值由文献[10]查阅和计算得到；超临界下密度的文献值根据Saul[11]推导得出的水的38参数状态方程计算得到。

从表3可以看出，模拟值与文献值很接近，最大相对误差不超过±10%，其精度基本能够达到工程设计计算的要求。比较文献值与模拟值可以看出，模拟的密度总体趋势比文献值要偏小。从表3数据还可以看出，在常态和亚临界状态下，温度是影响密度的主要因素，而压力对密度的影响较小；在超临界条件下，温度和压力的变化都会对密度产生较大的影响，但也依然保持了常态及亚临界条件下的随着温度升高密度减小，随着压力增大密度也随之增大的趋势。

超临界水密度是除偶极矩外决定其对有机溶剂溶解度大小的另一个重要因素；通常情况下，其密度增大，溶解度增大；密度减小，溶解度减小[12]。根据这一特性及超临界下水的密度随温度压力变化显著的特点，从而在实际应用过程中，可以通过调节温度压力来改变超临界水的溶解能力，进而达到萃取、分离等目的。

表3 水密度模拟值Table 3 The simulative density ofwater

3.2 水的自扩散系数计算

分子动力学模拟通过对研究物系中粒子的运动方程的求解从而得到粒子的运动速度和运动轨迹，通过统计计算即可求得扩散系数，由于是计算机实验，它能够不受高温高压的限制，对于计算超临界、深冷等特殊条件下的扩散系数其优势更加明显，因此它是研究扩散系数等传递性质的有效手段[13]。现今，基于MD计算溶液扩散系数主要有两种方法：一种是Einstein法，基于Einstein方程的，通过统计均方位移(MSD)与时间的变化，当时间足够长时，MSD与时间基本呈线性关系，从而计算斜率即可得到溶液扩散系数，其自扩散系数计算式如式1所示[14,15]。

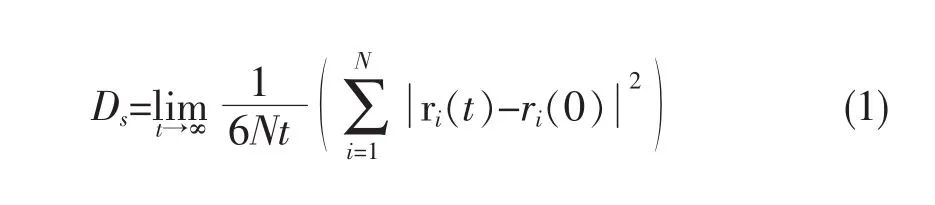
另一种是Green-Kubo法，通过计算体系中组分的速度相关函数再积分得到，其计算式如式2所示[14,15]。

由于Einstein法计算方法相对简便且准确性与Green-Kubo法相当，因此本文中的扩散系数采用Einstein方法进行计算。

本文用Einstein方法计算了不同温度、压力下水的自扩散系数，结果如表4所示。表4中常压及亚临界状态下扩散系数文献值由Krynicki[16]关联式计算得出；超临界条件下扩散系数文献值由Lamb[17]的实验数据公式拟合得到。

比较模拟值与文献值可知，水自扩散系数的模拟值与文献值的最大相对误差为-8.98%，其平均相对误差在±10%以内。因此在实验数据不足的情况下，用分子动力学模拟的方法来预测水的扩散系数是可行的[18]。从表4可以看出，从常态至超临界状态，水的自扩散系数都是随着温度的增加而增大，随着压力的增大而减小。与常态及亚临界条件相比，在超临界状态下，水有着更高的扩散系数，并且扩散系数随温度、压力的变化更加敏感。

表4 水的自扩散系数Table 4 The self-diffusion coefficient ofwater

3.3 水中氢键成键度

为了统计不同条件下的氢键变化情况，我们首先要给出合适的氢键成键标准。氢键的定义有分别按能量标准和按几何标准定义[19,20]，同时也有采用能量-几何混合的标准来定义[21]。本文由于是用坐标文件来统计氢键的，因此拟采用几何的标准来定义氢键。Teixeira[22]的中子衍射实验表明，当氢键偏离O-H键轴30°时，即图1中θ小于150°时，氢键将被破坏；通过水分子的径向分布函数研究表明，水分子间氧－氢间第一壳层的距离为2.4 A°，水分子内的氧－氢键距离为1.1 A°。为了编程统计过程的方便，从而我们定义氢键如下：如图1所示，当图1中∠ α≤30°并且R≤3.5 A°时氢键形成，当∠ α>30°，或 R>3.5 A°时氢键断裂，这一标准结合了本文体系的实际情况，同时也被众多国内外学者所采用[20,23]。

图1 水中氢键的定义Fig.1 The definition of H-bonds in water box

按照上述标准，本文采用VMD软件并结合Tcl/Tk编程，统计了不同温度、压力下水分子的成键度，结果如表5所示。从表5可以看出，298 K，0.1 MPa时，成键度为2.73，与Mas[24]用势函数SAPT-5s的计算值2.77很接近，但与Soper[25]测得该条件下的实验值3.58相比偏小，其主要原因还是现有水势能模型的准确性不足引起的。虽然结果与实验值有一定的偏差，但用于氢键估算和了解氢键变化规律是可行的。不论在何种条件下，随着温度的升高，压力减小，水的平均成键度减小；反之，成键度增加。可以看出，在超临界条件下，即使到了873 K，50 MPa下，水中仍然有少量的氢键存在，Gorbaty[26]也用实验证明了在超临界条件下仍有氢键的存在。现今，对于具体在什么情况下水中氢键会消失仍没有定论。

通常，每个水子可以形成1到5个氢键[27]。本文对不同条件下水分子各种氢键的概率做了统计，如表6所示。

表5 水中氢键的平均成键度Table5 The averagenumberofH-bonds perwatermolecule

从表6可以看出，在常态下，未形成氢键的水分子所占的比例很小；水分子主要形成了二至四个氢键的结构，占了70%以上。随着温度的升高，形成三、四、五个氢键的水分子数逐渐减少，而未成键和形成一、二个氢键的水分子数所占比例增加。与常态下相比，亚临界下未形成氢键的水分子数所占比例增幅明显，在接近超临界(633 K,22.05 MPa)时达到了33.05%。在亚临界相同压力下，温度升高使形成二、三、四、五个氢键的水分子数都减少，而未成键和形成一个氢键的水分子数增加；在亚临界相同温度下，随着压力的增加，未成键和形成一、二个氢键的水分子数有所减小，同时形成三、四、五个氢键的水分子数有所增加。到了超临界条件，形成5个氢键的水分子消失，与亚临界条件下相比未形成氢键的水分子数大幅增加，在873 K，50 MPa时达到了73%。在超临界相同压力下，温度升高使得形成各种类型氢键的水分子数都减少；而相同温度下，压力升高未成键水分子数减少，形成一、二、三、四个氢键的水分子数都有所增加。

表6 不同条件下各种氢键的概率Table 6 The probability of the different kinds of H-bonds in water

3.4 水表面张力的计算

表面张力通过压力张量的分量计算得到[28,29]，如式3：Pxx，Pyy，Pzz分别是系统压力张量在各个轴的分量，bar，Lz是模拟体系Z轴的长度，nm。通过单位换算即可得到水的表面张力。计算得到不同温度下水的表面张力如图2。图2中实线为Vargaftik[30]等人的实验值。从图2可以看出，模拟值与实验值相比都呈偏小的趋势，其原因可能是在计算过程中的简化计算，没有考虑氢键等因素对表面张力的影响，而水中却含有大量的氢键，从而使得模拟值比实验值偏小。

图2 水的表面张力Fig.2 The surface tension ofwater

4 结论

本文采用分子动力学方法对水的物性进行了模拟研究，其中水密度与自扩散系数的模拟值与文献值基本一致，可见采用分子动力学模拟方法来模拟预测水的性质是可行的。尤其当在超临界条件下实验数据难以测定时，分子动力学模拟的优势就更为明显。模拟结果表明：超临界下水的密度随温度压力的改变而变化显著，这一特性是超临界水用于萃取、分离有机溶剂的重要依据；水在超临界下比常态下有着更高的扩散能力。对水中的氢键计算结果表明：在常态下水中每个水分子平均形成的氢键数以二至四个氢键为主，占氢键总数的70%以上；然而随着温度的升高，每个水分子形成的氢键数减少。水表面张力模拟值比实验值小，其主要原因是计算过程未考虑氢键等因素对表面张力的影响。

[1]任华.分子模拟在界面相互作用计算中的应用 [D].西安：西北工业大学，2007.

[2]W.L.Jorgensen,J.Chandrasekhar,J.D.Madura,R.W.Impey,M.L.Klein.Comparison of simple potential functions for simulating liquid water[J].J.Chem.Phys.,1983,79,926-935.

[3]H.J.C.Berendsen,J.R.Grigera,and T.P.Straatsma.The Missing Term in Effective Pair Potentials[J].J.Phys.Chem.,1987,91:6269-6271.

[4]B.Hess,C.Kutzner,D.van der Spoel.GROMACS 4:Algorithms for Highly Efficient,Load-Balanced,and Scalable Molecular Simulation[J].J.Chem.Theory Comput.,2008,4:435-447.

[5]Berendsen,H.J.C.,Postma,J.P.M.,DiNola,A.,Haak,J.R.Molecular dynamicswith coupling to an external bath [J].J.Chem.Phys.1984,81:3684-3690.

[6]Bussi,G.,Donadio,D.,Parrinello,M.Canonical sampling through velocity rescaling [J].J.Chem.Phys.2007,126:014101.

[7]Essmann,U.,L.Perera,M.L.Berkowitz,T.Darden,H.Lee,and L.Pedersen.A smooth particlemesh ewald potential[J].J.Chem.Phys.,1995,103:8577-8592.

[8]T.Darden,D.York,L.Pedersen.Particle Mesh Ewald:An N-log(N)method for Ewald sums in large systems[J].J.Chem.Phys.,1993,98:10089-10092.

[9]Hess,B.,H.Bekker,H.Berendsen,and J.Fraaije.LINCS:A Linear Constraint Solver for molecular simulations [J].J.Comp.Chem.,1997.18:1463-1472.

[10]马沛生.化工热力学 [M].北京:化学工业出版社，2005.

[11]A.Saul,W.Wagner.A fundamental equation for water covering the range from the melting line to 1273 K at pressures up to 25000 MPa[J].J.Phys.Chem.Ref.Data,1989,18(4):1537-1564.

[12]杨润田，王志锋，张海峰，等.超临界水的应用及其环境中材料腐蚀的研究 [J].表面技术，2007，36(5):84-87.

[13]肖吉，陆九芳，陈健，李以圭.超临界水中气体扩散系数的分子动力学模拟 [J].高校化学工程学报，2001，15(1):6-10.

[14]H.Inomata,S.Saito,P.G.Debenedetti.Molecular Dynamics Simulation of Infinitely Dilute Solutions of Benzene in Supercritical CO2 [J].Fluid Phase Equilibria,1996,116:282-288.

[15]石剑.超临界CO2体系扩散系数的实验研究和分子动力学模拟 [D].天津:天津大学，2006.

[16]K.Krynicki, C.D.Green, D.W.Sawyer. Pressure and temperature dependence of self-diffusion in water[J].Faraday Discuss.Chem.Soc.,1978,66:199-208.

[17]W.J.Lamb,G.A.Hoffman,J.Jonas.Self-diffusion in compressed supercritical water[J].J.Chem.Phys.,1981,74(12):6875-6880.

[18]孙炜，黄素逸，王存文，池汝安.超临界水密度和自扩散系数预测的分子动力学模拟 [J].华中科技大学学报，2008，36(5):103-105.

[19]T.Lazaridis,M.Karplus.Orientational Correlations and Entropy in Liquid Water[J].J.Chem.Phys.,1996,105(10)：4294-4316.

[20]F.W.Starr,J.K.Nielsen,H.E.Stanley.Fast and Slow Dynamics of Hydrogen Bonds in Liquid Water [J].Phys.Rev.Lett.,1999,82(11):2294-2297.

[21]A.G.Kalinichev,S.V.Churakov.Size and topology of molecular clusters in supercritical water:a molecular dynamics simulation [J].Chemical Physics Letters,1999,302:411-417.

[22]J.Teixeira,M.C.Bellissent-Funel,S.H.Chen,Dynamics of water studied by neutron scattering [J].J.Phys.:Condens.Matter,1990,2:105-108.

[23]A.Luzar,D.Chandler.Hydrogen-bond kinetics in liquid water[J].Nature,1996,379(4):55-57.

[24]E.M.Mas,R.Bukowski,K.Szalewicz.Ab initio three-body interactions for water.II.Effects on structure and energetics of liquid[J].J.Chem.Phys.,2003,118(10):4404-4413.

[25]A.K.Soper,F.Bruni,M.A.Ricci.Site-site pair correlation functions of water from 25 to 400°C:Revised analysis of new and old diffraction data [J].J.Chem.Phys.,1997,106(1):247-254.

[26]Yu.E.Gorbaty, A.G.Kalinichev. Hydrogen Bonding in Supercritical Water.1.Experimental Results [J].J.Phys.Chem.,1995,99(15):5336-5340.

[27]张秀欣.液态水分子间氢键相互作用的从头分子动力学研究 [D].天津：河北工业大学，2007.

[28]C.A.Croxton,Statistical Mechanics of the Liquid Surface[M].John Wiley&Sons,Chichester,1980.

[29]N.J.P.Nijmeijer,A.F.Bakker,C.Bruin,et al.A molecular dynamics simulation of the Lennard-Jones liquid-vapor interface[J].J.Chem.Phys.,1988,89:3789-3792.

[30]N.B.Vargaftik,B.N.Volkov,L.D.Voljak.International Tables of the Surface Tension of Water[J].J.Phys.Chem.Ref.Data,1983,12(3):817-820.

Molecular Dynamics Simulation on Physical Properties of Water

WU Fangdi1ZHENG Huidong2WU Yanxiang2

(1.Department of Environment and Architecture Engineering，Wuyi University，Wuyishan，Fujian 354300;2.College of Chemistry and Chemical Engineering,Fuzhou University,Fuzhou，Fujian 350108)

The physical properties of water under different conditions were studied with SPC/Emodel by MD simulation.The density of supercritical water changed more significantly with the variation of temperature and pressure than that under subcritical and normal conditions,which is an important basis for supercritical water being used for extraction and separation of organic solvents.Moreover，supercritical water has higher diffusion ability than normal water.The studies showed that each water molecules mainly formed by two to four hydrogen bonds under normal condition.The number of hydrogen bonds in water reduced as the temperature increased.The simulation value of surface tension of water was smaller than experimental value for do not take into account the effects of H-bonds on the surface tension.

water;density;diffusion coefficient;degree of H-bond;surface tension;MD simulation

Q7

A

1674－2109(2011)05－0061－06

2011-09-07

吴方棣（1985-），男，汉族，助教，硕士，主要研究方向：传质与分离。