小棋盘大乾坤

221700 江苏省丰县王沟中学 蔡际红 刘广平

小棋盘大乾坤

221700 江苏省丰县王沟中学 蔡际红 刘广平

1 问题情境

围棋起源于公元前2000年的古代中国．从古代“井田制”到现代各种管、线、路的立体网络，再到虚拟如互联网络无不与棋盘世界相关．棋盘上最短走法问题是趣味数学问题常见问题，具有很好的教育功能．也是教材和教学实际的重要题材．要解决棋盘网络问题还得从数学入手．

2 原题呈现

在苏教版数学教材2－3计数原理导言部分设置了如下问题情境.

题1 如图1是某城市的街道．西北角是某同学的家，东南角是学校．问:从家经东西4条街、南北5条街(最短距离)，有几种不同的走法?

习题也多次出现由浅入深不同层次的练习题:

题2 (习题1．1T 9)如图2，从A处沿街道走到 B处，使路程最短的不同走法有多少种?

图1

图2 图3

题3 (习题1．1T10)如图3，从A处沿街道走到 B处，使路程最短的不同走法有多少种?

题 4 (习题 1．4T10)如图4，某地有南北街5道，东西街6道，一邮递员从该地西南角的邮局A出发，送信到东北角的B地，且途经C地，要求所走路程最短，共有多少种不同的走法?

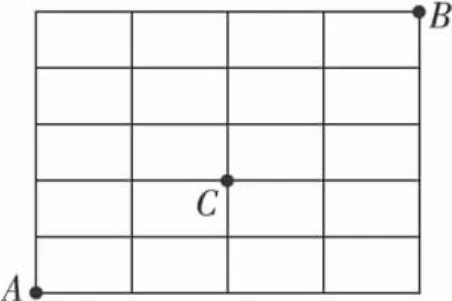
图4

3 推广探究

3．1 问题综述

如图5，由m+1条等距a的水平直线和n+1条等距b的竖直直线组成的图形，称为(m+1)×(n +1)棋盘，也称为 m×n格棋盘．从左下角 A0，0到右上角 Am+1，n+1的最短路程为ma+nb．求走最短路线的方法有多少种．

图5

问题可以推广为从任意点到任意点的走法，及经过某点的走法．

格点记法:记A点为A0，0，第i行第j列的格点记为Ai，j．从 A0，0点到 Ai，j的最短走法数记为 ai，j．

3．2 解法探求

爱因斯坦说过“有待探索的自然界是有规律的，相信基本规律是简明单纯的”，此问题亦不例外．

3．2．1 归纳猜想法

3．2．2 递推公式法

③式我们称为递推公式，从①，②出发，运用③递推，即可求出任何 ai，j对应 .

3．2．3 杨辉三角形

观察图6中数字特点，如图7:

图6 图7

4 结论推广

图9

5 结论应用

5．2 应用举例

例1 (2010苏北四市第三次调研考试第23题)如图10，在某城市中，两地之间有整齐的方格形道路网，其中A1，A2，A3，A4是道路网中位于

一条对角线上的4个交汇处．今在道路网M，N处的甲、乙两人分别要到N，M处，他们分别随机地选择一条沿街的最短路径，以相同的速度同时出发，直到到达N，M为止．

(1)求甲经过A2到达N的方法有多少种;

(2)求甲、乙两人在A2处相遇的概率;

(3)求甲、乙两人相遇的概率．

解 (1)甲经过A2，可分为两步:

第一步，甲从M经过A2的方法数为C13种;

图10

例2 (1)一只蚂蚁沿着正方体ABCD—A1B1C1D1的棱布设管道，由A点出发沿棱到C1，路程最短的走法有多少种?

(2)若沿二阶魔方(8个小正方体)的棱呢?

(3)若沿三阶魔方(27个小正方体)的棱由A点出发沿棱到C1，求蚂蚁由A点出发途经B点到C1的概率是多少?

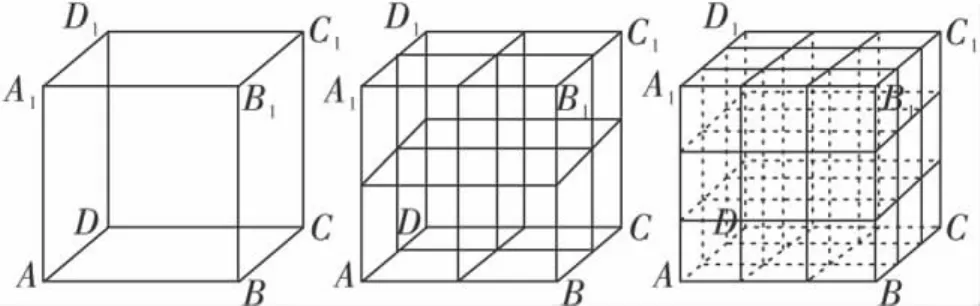
图11

6 延伸思考

课本是最重要的教学资源，我们应充分挖掘课本习题的丰富内涵，通过拓展、延伸、类比、联想发现并证明新结论，形成数学模型，并利用它解决新问题，实现课本资源利用的最大化．我们要揭开表象把握实质，积极应用数学模型优化解决．同时对激发学生兴趣、培养学生的创新能力和理性精神均有裨益．正可谓:

棋盘虽小，

内藏乾坤;

课本朴素，

内涵精深;

联想思考，

探求规律;

得“意”忘“形”，求其精神．

1 裘宗沪．趣味数学三百题．北京:中国少年儿童出版社，1984

20110504)