基于结构方程的区域旅游产业竞争力评价模型

喻胜华， 杨 薇

（1．湖南大学经济与贸易学院，湖南长沙410079；2．武汉生物工程学院计算机与信息工程系，湖北 武汉430415）

基于结构方程的区域旅游产业竞争力评价模型

喻胜华1， 杨 薇2

（1．湖南大学经济与贸易学院，湖南长沙410079；
2．武汉生物工程学院计算机与信息工程系，湖北 武汉430415）

文章从系统分析评价区域旅游产业竞争力的传统统计分析方法的优劣出发，借助结构方程模型来研究资源因素、支持因素、区域旅游管理因素、区位因素及需求状况因素五个因素与区域旅游产业竞争力之间的关系。采用对称量表形式，通过现场调查和发送电子邮件等方式完成研究所需要的数据收集，并在此基础上建立了拟合优度更好的区域旅游产业竞争力评价模型。研究表明，上述五个因素与区域旅游产业竞争力之间均存在正相关关系，其中旅游需求对区域旅游产业竞争力的影响最大，其次为支持因素。

结构方程；区域旅游；竞争力评价

一、引 言

目前，随着我国经济的飞速发展，旅游业作为伴随着我国改革开放而发展起来的一项新兴产业也得到了快速的发展，并已成为许多地区经济发展的支柱产业之一。提升我国旅游产业的核心竞争力，把旅游业做大做强已成为我国经济发展的一项长期战略。近10年来，我国学者对如何科学评价旅游产业竞争力开展了广泛的研究。从研究方法来看，已往研究主要应用了层次分析法、数据包络法、主成分分析法、多变量方差分析、相关性分析、复回归分析、路径分析等方法［1］［2］［3］［4］［5］［6］［7］。这些方法有可取之处，但是缺点也比较明显：大多数方法只能在同一时间内检验单一的自变量与因变量关系，而且这些分析方法往往存在理论上的假设限制及使用缺陷。层次分析法依赖专家的判断但容易造成主观臆断；因子分析能反映变量与变量之间的关系，但无法进一步分析变量间的因果关系；路径分析虽然可以分析变量间的因果关系，但实际情况却难以符合其变量之间的测量误差为零、残差之间不相关、因果关系为单向等基本假设。为弥补上述方法缺陷的必要性，本文借助结构方程模型来分析资源因素、支持因素、区域旅游管理因素、区位因素及需求状况因素等五因素与区域旅游产业竞争力之间的关系。解决变量的量化问题，从而使结论更具有客观性和全面性。此外，易丽蓉的研究中采集样本的范围局限于重庆市，这会在一定程度上影响模型的精度和适应范围，并且该文献最终的模型结构较复杂，未对模型进行修正［8］。因此，本文拟在此基础上对结构方程模型作进一步的重构和精简，并根据最终的通径图，得到了旅游产业竞争力评价的数学模型。

二、理论模型的构建

结构方程模型是一种通用的线性统计建模技术，广泛应用于心理学、经济学、社会学和管理科学等领域，与层次分析、因子分析及路径分析等传统方法相比，结构方程模型有着明显的优势。层次分析法易造成主观臆断，因子分析法无法分析变量间的因果关系，而路径分析虽然可以分析变量间的因果关系，但实际情况却难以符合其变量之间的测量误差为零、残差之间不相关、因果关系为单向等基本假设。结构方程模型可以弥补这些方法的不足之处。

结构方程模型包含两个部分：结构模型和测量模型，结构模型反映潜变量之间的因果关系，亦称潜变量模型，其模型形式为：

其中，η、ξ分别是内生潜变量向量和外生潜变量向量；B、τ分别为内生潜变量和外生潜变量的通径系数矩阵；ζ为随机误差向量，反映了η未能被解释的部分。

测量模型用以描述潜变量和可测变量之间的关系，其模型形式为：

其中，x是ξ的观测指标，y是η的观测指标，δ是x的观测误差向量，ε是y的观测误差向量。Λx是由x在ξ上的因子负荷构成的矩阵，Λy是由y在η上的因子负荷构成的矩阵。

三、旅游竞争力评价模型的构建与修正

1．变量设置

本文首先以“区域旅游产业竞争力五因素模型”为基础构建初步的结构方程模型，然后对此模型作进一步的修正，从而得到最终模型。设模型包括2个外生潜变量：旅游资源（zy）和支持因素（zcys）；4个内生潜变量：旅游需求（xq）、区域旅游竞争力（jzl）、区域旅游管理（gl）和区位条件（qw）。其中，zy的可测变量为：自然资源（x1）、人文资源（x2）和游乐基础设施资源（x3）；zcys的可测变量为：旅游地一般基础设施（x4）、服务质量（x5）和季节是否合适（x6）；xq的可测变量为：旅游地的整体形象（y1）、旅游地特产的向往（y2）和个人的偏好（y3）；jzl的可测变量为：旅游地的游客人数（y4）和旅游地的游客人数增长率（y5）；gl的可测变量为：旅游地的环境（y6）、旅游地的管理（y7）和旅游目的地的营销方式（y8）；qw的可测变量为：邻近效应（y9）和交通的便利性（y10）。

2．初始模型

本文采用对称量表形式，将问卷评分级度划分为七等：完全不重要、不重要、不太重要、重要、比较重要、很重要、特别重要。同时赋予每个评分级度相应的分值，分别为1～7。通过现场调查和发送电子邮件等方式来完成研究所需要的数据收集，共收到有效问卷236份。首先采用SPSS13．0统计软件计算每个观测变量的最小值、最大值、平均数、标准差、偏度及峰度，计算结果表明每1个指标的偏度值和峰度值的范围都在－2与＋2之间，所以满足正态分布的要求，再采用内部一致性这一指数对量表信度进行检验，一般来说，Cronbach’sα值大于0．7为高信度，小于0．35为低信度，0．5为最低可以接受的信度水平。本文中数据的Cronbach’sα值大于0．7，说明本问卷的信度比较好。具体数值如表1所示。

表1 信度检验表

将收集的数据输入到LISREL 8．51，并采用预先编好的LISREL语法文件，结果如图1所示。

图1 初始模型的通径图

从图1初始模型的通径图可以看出，卡方值为194．36，自由度为74，相应的p值为0．003 3，表明卡方值显著。近似误差的均方根RMSEA为0．073（小于0．08），拟合优度指数GFI达到了0．90，说明模型较好地拟合了样本数据。但比较拟合指数CFI（0．85）和规范拟合指数NFI（0．76）都未达到0．90以上，所以模型还需要进一步修正。为方便起见，我们把上述初始模型记为M1。

3．模型的修正

模型M1的输出结果表明，模型中可能错误地设定了没有影响性的因果关系。为此，我们考虑两种精简模型：即剔除区位条件与需求状况影响的修正模型M2，同时剔除区位条件与需求状况影响和区域旅游管理与需求状况的影响的修正模型M3。由于修正模型M2和修正模型M3都是初始模型M1的“嵌套”模型，所以对这3个模型进行比较时，要运用似然比检验，用2个模型拟合的卡方值之差作为新的卡方值，用2个模型的自由度之差作为新的自由度。在检验的结果中，如果增加自由参数后，卡方值显著减少，说明增加自由参数是值得的；如果减少自由参数后，卡方值没有显著地增加，说明减少自由参数是可取的。修正模型M2和修正模型M3的各输出结果如表2所示。从表2可以看出，相比较而言，修正模型M3的卡方值最小，而GFI值和CFI值最大，且接近0．90，说明修正模型M3拟合得更好，所以，我们最终确定的最佳模型为修正模型M3，这也符合模型选择的简约性原则。修正模型M3相应的通径图如图2所示。由图2中的因子负荷和通径系数可写出区域旅游产业竞争力评价的数学模型，即：

其中，jzl（1）和jzl（2）分别为区域旅游产业竞争力的实际值和理论值，其他各变量关于对应指标的线性关系式可类似写出。

我们先通过专家评分法得到每个评价指标的分值，然后由（4）式计算出区域旅游产业竞争力的实际值，再由各潜变量的分值及（5）式得到区域旅游产业竞争力的理论值，在实际评价的过程中，如果实际得分高于理论得分，则认为该区域的旅游产业竞争力较高，反之，如果理论得分高于实际得分，则认为该区域的旅游产业竞争力较低。

表2 修正模型和初始模型的拟合指数对比

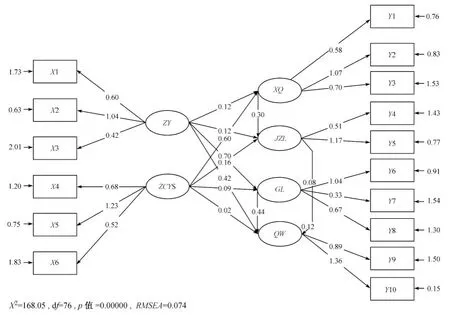
图2 模型M3的通径图

四、结 论

由第三部分的表达式（5）可知，旅游资源、支持因素、旅游管理、旅游需求以及区位条件等五个影响因子与区域旅游竞争力之间均存在正相关关系，其中，旅游需求对区域旅游竞争力的影响最大，其次为支持因素。由于各因素对区域旅游竞争力的影响相差不大，因此其他因素的影响也不能忽略，而要综合考虑各种因素，以全面提升区域的旅游竞争力。

［1］万绪才，李刚，张安．区域旅游业国际竞争力定量评价理论与实践研究［J］．经济地理，2001，21（3）：355-358．

［2］张欣．旅游产业区域竞争力的理论研究和实施分析［D］．青岛：青岛大学硕士论文，2002．

［3］杨森林，郭鲁芳，王莹．中国旅游业国际竞争策略［M］．上海：立信会计出版社，1999．18-36．

［4］黎洁，赵西萍．论国际旅游竞争力［J］．商业经济与管理，1999，19（4）：63-66．

［5］冯茂娥．陕西省旅游业国际竞争力测评与提升战略研究［D］．西安：陕西师范大学硕士论文，2003．

［6］张争胜，周永章．城市旅游竞争力的实证研究以广东省为例［J］．资源开发与市场，2005，21（1）：13-17．

［7］黄秀娟．旅游产业竞争力研究综述［J］．福建农林大学学报（哲学社会科学版），2007，10（2）：53-59．

［8］易丽蓉．基于结构方程模型的区域旅游产业竞争力评价［J］．重庆大学学报（自然科学版），2006，29（10）：154-158．

The Evaluation Model of Regional Tourism Industry Competition via Structural Equation

YU Sheng-hua1， YANG Wei2
（1．College of Economics and Trade，Hunan University，Changsha 410079，China；
2．Department of Computer and Information Engineering，Wuhan Bioengineering Institute，Wuhan 430415，China）

The paper examined the relationship between the regional tourism industry competitiveness and the five factors such as resources，support，regional tourism management，location and demand by analyzing the strengths and weaknesses of the traditional statistical analysis methods for evaluating the regional tourism industry competitiveness，with the merits of structural equation model．Using the symmetric scale，data collection was obtained through investigation and E-mail，etc．Based on the data，the evaluation model was developed about regional tourism industry competitiveness with better fitness．From the final route chart it can be seen that there are positive correlation between any one of the above five factors and the regional tourism industry competitiveness．Among them the tourism demand has the biggest influence on the regional tourism industry competitiveness，and the next is support factor．

structural equation；regional tourism；evaluation of competition

F590；F224．0

F069

1008-407X（2011）04-0044-04

2011－04－23；

2011－08－10

喻胜华（1966-），男，湖南宁乡人，教授，博士，主要从事数量经济学研究；杨薇（1985-），女，湖南衡阳人，助教，主要从事数量经济学研究。