不含4-圈的平面图的L( p, q)-标号
2011-01-12朱海洋盛景军侯立峰葛生联
朱海洋,盛景军,侯立峰,葛生联
(徐州空军学院后勤指挥系,江苏徐州 221000)
不含4-圈的平面图的L(p,q)-标号
朱海洋,盛景军,侯立峰,葛生联
(徐州空军学院后勤指挥系,江苏徐州 221000)
令G为平面图,用Δ(G)和λp,q(G)分别表示G的最大度和L(p,q)−标号数,其中p和q是满足p≥q的两个正整数.证明了若G为Δ(G)≤5且不含4-圈的平面图,则λp,q(G) ≤ (2q−1)Δ (G)+ 8p+ 14q− 11.这一结论改进了有关文献的相关结果.
平面图;4-圈;L(p,q)-标号
所有图均为无向连通简单图.对于图G,令V(G)、E(G)、Δ(G)和δ(G)分别为图的顶点集合、边集合、最大度和最小度,如果图G能画在曲面S上使它的边仅在端点处相交,则称G可嵌入曲面S.若图G可嵌入平面,则称G是平面图.平图是平面图在平面上的一个嵌入.dG(u,v)表示顶点u,v之间的距离.图G的围长g(G)是G中最短圈的长度.图G的平方图记为G2,指的是一个图满足以下条件:V(G2) =V(G)并且uv∈E(G2),当且仅当1≤dG(u,v) ≤ 2.图G的正常k−顶点染色是映射f:V(G) → {1,L ,k},其中f满足对任意的相邻顶点u,v,都有f(u) ≠f(v),最小的整数k称为图G的色数,记为χ(G),由 Brooks定理,对于任意图G,χ(G2) ≤Δ2(G)+ 1,这个上界是紧的,Petersen图和5-圈就是两个最简单的例子.其它未定义的符号见文献[1].
定义1 设p和q是满足p≥q的两个正整数.图G的k−L(p,q)−标号是一个映射ϕ:V(G) → {0,1, L,k} ,其中ϕ满足对任意的u,v∈V(G),若dG(u,v) = 1,则p;若dG(u,v)= 2,则 |ϕ(u)−ϕ(v)|≥q.图G的L(p,q)−标号数是使G存在k−L(p,q)−标号的最小的整数k,记为λp,q(G).图G的L(1,1)−标号等价于图G2的正常顶点染色,且λ(G)=χ(G2) −1.
1,1
Wegner[2]首先研究了平面图的平方图的色数,证明了若G为 Δ (G) = 3的平面图,则χ(G2) ≤ 8,并且提出以下著名猜想:
猜想1 设G为平面图,若 4 ≤Δ (G)≤7,则χ(G2) ≤Δ (G)+5;若 Δ (G)≥8,则

1 引理及其证明


证明:假设引理1不正确,设G为 Δ (G)≤ 5且不含4-圈的平图,为不含构型(A1)–(A10)的一个反例.由于G无4-圈,所以G中不存在两个相邻3-面,且每个顶点u至多关联 ⎢⎣d(u)/2⎥⎦个 3-面.由于假设G不含构型(A1)和(A2),所以δ(G) ≥ 2且G中任意3-面都不关联任何2-点.由假设G不含构型(A3),所以G中不存在一条边uv∈E(G)使d(u) = 2和d(v)≤4.由于假设G不含构型(A4),所以G中不存在一条边uv∈E(G)使d(u) =d(v) = 3.由于假设G不含构型(A5),所以G中不存在一条关联某个 3-面的边uv∈E(G)使d(u)=4,d(v)=3.下面给出所使用的重新分配顶点和面的权转移规则:
(R1)每个5+−面f转移权1/5给每个相关联的点;
(R2)每个5−点u转移权4/5给每个相邻的2-点;
(R3)每个4+−点u转移权1/5给每个相邻的3-点;
(R4)每个4−点u转移权1/5给每个相关联的3-面;
(R5)设u是一个5-点和f是它的关联3-面.若f是一个(5,5,5)−面,则u转移权1/3给f;否则u转移权3/5给f.
设w′表示结果权函数,只需证明对任意的x∈V(G)UF(G),均有w′(x)≥ 0.
下面首先考察任意面f∈F(G)的新权.

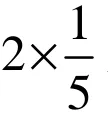
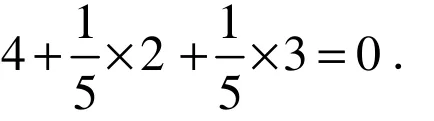
情况3 若d(u)=4.设x,y,z,t是u的邻点.由于假设G不含(A3),所以x,y,z,t均为3+−点.
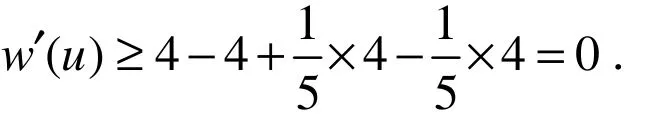
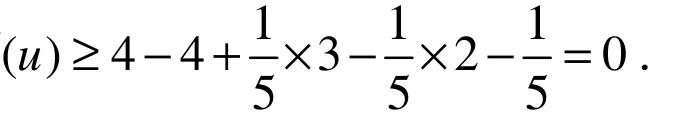
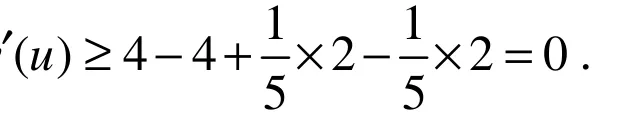
情况 4 若d(u)=5.设x,y,z,t,w是u的邻点.由假设G不含(A7),所以u至多相邻 2个2-点.
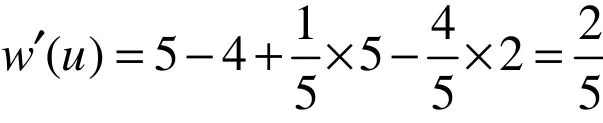
情况4.2 假设u只关联1个3-面,那么u关联4个5+−面.不妨设 [ ]f=uxy为该3-面.因为G不含构型(A2),所以x,y均为3+−点.因为G不含构型(A4),所以{x,y}中至多存在1个3−点.因为G不含构型(A8),所以{z,t,w}中至多存在1个2-点.
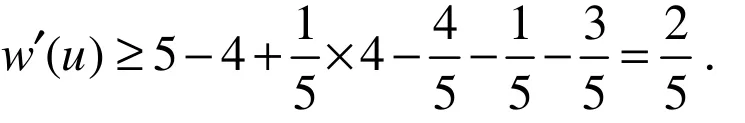

情况4.3 假设u只关联2个3-面,那么u关联3个5+−面.不妨设f1=[uxy]和f2=[uzt]为关联u的3-面.因为G不含构型(A2),所以x,y,z,t均为3+−点.因为G不含构型(A4),所以{x,y}中至多存在1个3−点,{z,t}中至多存在1个3−点.
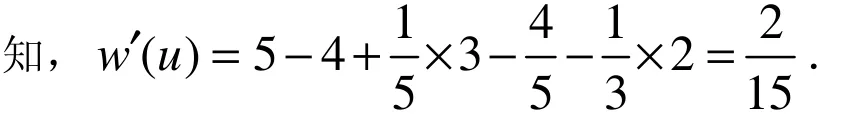
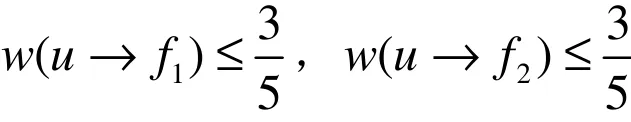
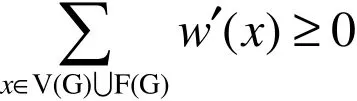
2 定理1的证明


定理1的证明:采用反证法.
假设定理1不成立.选取G为满足假定条件且λp,q(G)>n的边数|E(G)|尽可能小的平面图,其中n= (2q−1)Δ (G)+ 8p+ 14q− 11 = 4(2p−1)+ (2q−1)(Δ (G)+ 7).记L= {0,1,L ,n}.
由引理1知,G包含满足构型(A1)–(A10)之一的顶点u.假设u1,L ,uk为u的邻点,且d(u1)≤d(u2) ≤L≤d(uk).若(A1)或(A2)成立,令H=G−u.若(A3)或(A4)或(A7)成立,令H=G−uu1.若(A5)或(A6)成立,令H=G−ux.若(A8)或(A9)成立,令H=G−uw.若(A10)成立,不妨设d(x) =d(z) = 3,令H=G−ux.显然,H是不含4-圈的平面图,且 Δ (H) ≤Δ (G),|E(H)|<|E(G)|.由于G的边数的极小性,λp,q(H)≤n,因此H存在一个以L为标号集合的n−L(p,q)−标号.设该映射为φ,下面给G进行标号.
情形1 若(A1)成立,将φ限制到图G上.因为|F(u)|≤ (2p−1)+ (2q−1)(Δ (G)−1) 情形2 若(A2)成立,将φ限制到图G上,因为|F(u)|≤ 2(2p−1)+ (2q− 1)(d(u1)−2+d(u2)−2) ≤ 2(2p−1)+ (2q− 1)(5 −2 +Δ (G)−2) 情形 3 若(A3)成立,将φ限制到图G上,现去掉u和u1的原有标号,依次给u1和u重新标号.设xi为u1的不同于u的邻点,其中i=1,L ,d(u1)−1.那么 |F(u1)|≤(d(u1)−1) (2p−1)+(2q− 1)(d(u)−1+d(x1)−1 +L+d(xd(u1)−1)−1).因为d(u1) ≤ 4,所以 |F(u1)|≤3(2p−1)+ (2q− 1)(2− 1+ 5− 1+ 5− 1 +Δ (G)−1)≤n.令φ(u1)∈LF(u1).由于F(u)≤ 2(2q−1) + (2q− 1)(d(u1)−1 +d(u2)− 1) ≤ 2(2q−1)+ (2q− 1)(4− 1 +Δ (G)−1) 情形4 若(A4)成立,将φ限制到图G上.首先去掉u和u1的标号,然后依次给u和u1进行重新标号.由于 |F(u)|≤ 2(2p−1)+(2q− 1)(∑i=1,2,3(d(ui)−1)) ≤ 2(2p−1)+(2q−1)(2 +4+ Δ (G)− 1) 情形5 若(A5)成立,将φ限制到图G上.首先取消u和x的标号,然后依次给u和x进行重新标号.设z,w为u的不同于x,y的邻点.因为|F(u)|≤ 3(2p−1) +(2q− 1)(d(x) −2+d(y) −2 +d(z)−1 +d(w) −1) ≤ 3(2p−1) + (2q− 1)(3 −2 +5 −2 +5 −1 +Δ (G)−1) 情形6 若(A6)成立,将φ限制到图G上.首先取消u和x的标号,然后依次给u和x进行重新标号.因|F(u)|≤ 3(2p−1)+ (2q− 1)(d(x) −2 +d(y) −2 +5− 1 +Δ (G)−1) ≤ 3(2p−1)+ (2q− 1)(2 +2 +4 +Δ (G)−1) 情形7 若(A7)成立,将φ限制到图G上.首先取消u,u1,u2的标号,然后依次给u,u1,u2进行标号.因为 |F(u)|≤ 3(2p−1)+(2q− 1)(∑i=1,L,5(d(ui)−1)) ≤ 3(2p−1)+(2q−1)(1+ 1+ 3+ 4 +Δ (G)− 1) ≤n,令φ(u)∈LF(u).其次给u1,u2进行标号,因为|F(ui)|≤2(2p−1)+ (2q− 1)(Δ (G)−1 + 4) 情形8 若(A8)成立,将φ限制到图G上.首先取消u,t,w的标号,然后依次给u,t,w重新标号.设z为u的不同于x,y,t,w的邻点.因为|F(u)|≤ 3(2p−1) +(2q− 1)(d(x) −2 +d(y)−2 +d(t) −1 +d(w) −1 +d(z) −1) ≤ 3(2p−1)+ (2q− 1)(3 +3 +2+ 1 +Δ (G)−1)≤n,令φ(u)∈LF(u).其次给t进行标号,因为|F(t)|≤ 3(2p− 1)+(2q− 1)(5− 1+ 5− 1 +Δ (G)− 1) 情形9 若(A9)成立,将φ限制到图G上,首先取消u,w的原有标号,然后依次给u,w重新标号.不妨设d(x)≤4.由于|F(u)|≤ 4(2p−1) + (2q− 1)(d(x) −2 +d(y) −2 +d(t) −2+d(z)− 2+d(w)− 1)≤4(2p−1)+ (2q− 1)(2 +3 +3 +Δ (G)−2+ 1)=n,令φ(u)∈LF(u).最后给w进行标号,因为|F(w) |≤ 2(2p− 1)+(2q− 1)(5− 1 +Δ (G)− 1) 情形10 若(A10)成立,不妨设d(x) =d(z) = 3,令H=G−ux.设w为u的不同于x,y,z,t的邻点.将φ限制到图G上.首先取消u,x,z的标号,然后依次给u,x,z重新标号.因为|F(u)|≤ 3(2p−1)+(2q− 1)(d(x) −2 +d(y) −2 +d(t) −2 +d(z) −2 +d(w) −1) ≤ 3(2p−1)+ (2q− 1)(1+ 3 +3+ 1 +Δ (G)− 1) 这样,每一种情况φ都可以扩展到G的以L为标号集合的n−L(p,q)−标号,所以λp,q(G)≤n,这与λp,q(G)>n相矛盾.证毕. [1]West D B. 图论导引[M]. 李建中, 骆吉洲, 译. 2版. 北京: 机械工业出版社, 2006: 10-20. [2]Wegner G. Graphs with given diameter and coloring problem [R]. Dortmund: Department of Mathematics, University of Dortmund, 1977: 1-10. [3]Thomassen C. Applications of Tutte cycles [R]. Copenhagen: Department of Mathematics, Technical University of Denmark, 2001: 1-20. [4]Heuvel J V D, Mcguiness S. Coloring the square of a planar graph [J]. Journal of Graph Theory, 2003, 42: 110-124. [5]Molly M, Salanatipour M R. A bound on the chromatic number of the square of a planar graph [J]. Journal of Combinatorial Theory: B, 2005, 94: 189-213. [6]Wang W F, Lih K W. Labeling planar graphs with conditions on girth and distance two [J]. SIAM Journal on Discrete Mathematics, 2003, 17(2): 264-275. [7]Wang W F, Cai L Z. Labeling planar graphs without 4-cycles with a condition on distance two [J]. Discrete Applied Mathematics, 2008, 156: 2241-2249. [8]Borodin O V, Ivanova A O. 2-distance (Δ+2)-coloring of planar graphs with girth six and Δ (G)≥ 18 [J]. Discrete Mathematics, 2009, 309: 6496-6502. L(p,q)-Labeling of Planar Graphs without 4-Cycles ZHU Haiyang, SHENG Jingjun, HOU Lifeng, GE Shenglian LetGbe a planar graph,p,qbe two positive integers withp≥q, Δ(G) andλp,q(G) denote respectively the maximum degree and theL(p,q)-labeling number ofG. Then,λp,q(G)≤ (2q− 1) Δ (G)+ 8p+ 14q− 11 could be achieved ifGbe a planar graph with Δ (G) ≤ 5 and without 4-cycles. The result improves previous results for the planar graphGwith Δ (G) ≤ 5 and without 4-cycles. Planar Graph; 4-Cycles;L(p,q)-Labeling (编辑:王一芳) O157.5 A 1674-3563(2011)02-0019-08 10.3875/j.issn.1674-3563.2011.02.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得 2010-07-05 朱海洋(1979- ),男,吉林白城人,助教,硕士,研究方向:图论与军事运筹学
(Department of Logistics Command, Xuzhou Air Force College of PLA, Xuzhou, China 221000)
