二阶椭圆问题的格林函数双线性矩形元的超收敛性

张兴军，何文明

(温州大学数学与信息科学学院，浙江温州 310035)

二阶椭圆问题的格林函数双线性矩形元的超收敛性

张兴军，何文明

(温州大学数学与信息科学学院，浙江温州 310035)

把二维二阶椭圆问题的格林函数的双线性矩形元的逐点误差估计与一般二阶椭圆问题的一次线性元的超收敛性结合起来，对二维二阶椭圆问题的格林函数的双线性矩形元的超收敛性进行了研究，得到了相应的逐点误差估计.

二阶椭圆问题；格林函数；双线性矩形元；逐点误差估计；超收敛性

考虑如下的二阶椭圆问题：

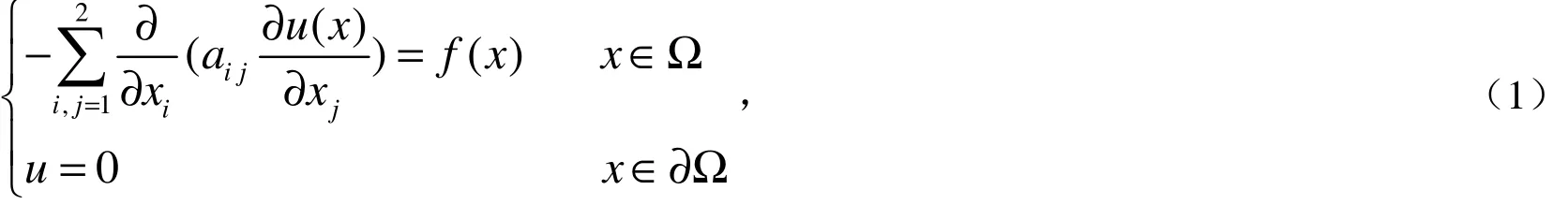
设x0∈Ω，（1）式在点x0的格林函数被定义为[1-2]：

如果采用内积的方法，则(x)可以被定义为：

这里A(u,v)被定义为：

由于在一般情况下不能得到方程（1）的解析解，因此有限元等数值方法就成为求解（1）的有效工具.近年来，有限元的超收敛性很受关注，有些文献是通过研究其相应格林函数的有限元的逐点估计来观察有限元的超收敛性的[3-5].设Th为区域Ω的一致矩形部分，由文献[3]和文献[6]得到如下的超收敛性结果：

本文运用研究一般椭圆问题的有限元方法的超收敛性的方法[9]来对（1）的格林函数双线性矩形元的超收敛性进行研究，得到如下结果：

注：本文中，c表示常数，c在各个地方的取值可以不一样，但都与h无关.

1 主要结果

本节要用到如下3个基本结果：

引理2[4]设Th为定义在区域Ω上的一致矩形剖分，而是∂xGx基于Th的双线性矩形元近似，则

引理3 在引理2的条件下有：

本文的主要结果如下：

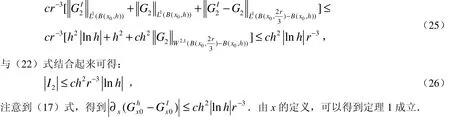
2 数值算例

[1]谢锐锋. 凹角域上Green函数逼近的逐点估计与有限元外推[J]. 计算数学, 1988, 10(3): 232-241.

[2]Krasovskii J P. Isolation of singularities of the Green’s function [J]. Mathematics of the USSR-Izvestiya, 1967, 1(5): 935-966.

[3]林群, 朱起定. 有限元的预处理与后处理[M]. 上海: 上海科学技术出版社, 1994: 80-89.

[4]朱起定, 林群. 有限元的超收敛理论[M]. 长沙: 湖南科学技术出版社, 1989: 73-79.

[5]朱起定. 有限元法的逐点估计及最大模内估计[J]. 计算数学, 1981, 3(1): 87-90.

[6]陈传淼, 黄云清. 有限元高精度理论[M]. 长沙: 湖南科学技术出版社, 1995: 47-53.

[7]Schtaz A H, Wahlbin L B. Interior maximum norm estimates for finite element methods [J]. Mathematics of Computation, 1995, 64: 414-442.

[8]Wahlbin L B. Superconvergence in Galerkin Finite Finite Element Methods [M]. New York: Springer Press, 1995: 166-195.

[9]何文明, 崔俊芝, 朱起定. 一种改进的超收敛与外推的方法[J]. 计算数学, 2002, 24(3): 327-334.

[10]He W M. Error estimates of finite element method about elliptic problems with singular righthand side [J]. Applied Mathematics and Computation, 2007, 188(1): 824-832.

[11]Zhu Q D. Superconvergence analysis for cubic triangular element of the finite element [J]. Journal of Computational Mathematice, 2000, 18(5): 541-550.

[12]Zhu Q D, Zhao Q H. New Discussions for Finite Element Superconvergence [J]. Advances in Mathematics, 2004, 33(4): 453-466.

Super-convergence of Bilinear Rectangular Element of Green’s Function in Second Order Elliptic Problems

ZHANG Xingjun, HE Wenming
(College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)

By combining pointwise error estimates of bilinear rectangular element of Green’s function in two-dimensional second order elliptic problems with super-convergence of one order linear element of common second order elliptic problems, the super-convergence of bilinear rectangular element of Green’s function in two-dimensional second order elliptic problems was examined. And the corresponding pointwise error estimates were obtained at the same time.

Second Order Elliptic Problem; Green Function; Bilinear Rectangular Element; Pointwise Error Estimate; Super-convergence

(编辑：王一芳)

O175.2

A

1674-3563(2011)02-0007-06

10.3875/j.issn.1674-3563.2011.02.002 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2010-05-27

张兴军(1984- )，男，贵州遵义人，硕士研究生，研究方向：偏微分方程

book=0,ebook=168