东方气田海管悬跨段安全评估分析

姚 平, 范奉鑫, 李中阳, 李 磊, 曹玉龙, 刘 洋

(1．中海石油(中国)有限公司湛江分公司生产部, 广东 湛江 524057; 2．中国科学院 海洋地质与环境重点实验室, 山东 青岛 266071; 3．中国科学院 力学研究所 环境力学重点实验室, 北京 100190)

东方气田海管悬跨段安全评估分析

姚 平1, 范奉鑫2, 李中阳3, 李 磊3, 曹玉龙3, 刘 洋3

(1．中海石油(中国)有限公司湛江分公司生产部, 广东 湛江 524057; 2．中国科学院 海洋地质与环境重点实验室, 山东 青岛 266071; 3．中国科学院 力学研究所 环境力学重点实验室, 北京 100190)

从工程实际问题出发, 利用实际测量资料, 通过建立近底床悬跨海管的有限元模型, 计算了不同底床形状下海管最大静挠度随海流流速变化的规律, 对东方 1-1气田某标段海管进行了安全评估,筛选出了危险悬跨段。这一计算结果对海管的防护维护工程实践具有切实的指导意义。

东方1-1气田; 海底悬跨管线; 评估分析; 有限元模型; 沙波

海底管道自从1954年正式投入运行, 就以其经济性和便利性, 迅速成为海上石油天然气集输的重要设施, 被誉为海上油气开发的生命线。海底管线的安全与否直接影响海上油气运输的经济效益和生态环境。位于南海北部湾海域的东方1-1气田是中国海洋石油有限公司目前最大的自营气田。由于该海域海底沙脊沙波异常活跃, 非常容易造成海底管道悬跨, 海管在悬跨段很容易发生弯曲变形。为保证管道安全运行, 中海油每年都要进行潜水探测, 随时了解海管情况, 尤其是台风过后海管的悬跨状况。为了研究海管跨长与弯曲应力的关系, 很多学者提出数值模型来进行分析。Mouselli[1]提出了CAM方法, 通过管道强度准则来判断海管静态临界安全跨长。王维[2]提出了弯矩修正法, 在管道模型的边界条件中加入约束, 以此来模拟埋设段对选跨段的影响。但是上述的学者研究都没有考虑水动力的影响, 而实际情况中海管悬跨段受到海水流动的水动力影响十分显著。本文以某次探测结果为例, 建立起考虑水动力影响的数值模型。并通过有限元计算, 分析各悬跨段的安全状况, 指出可能出现危险的跨段。

1 模型参数

由于本文中建立起的数值模型是基于实际工程需要, 因此在建立模型之前需要将海管悬跨数据与设计数据进行整理。表1、表2所列的是东方1-1气田中的某条海管的设计参数和实际探测结果。该条海管总长约 150 km, 由西向东铺设, 西侧海管埋在沙中, 东侧海管平放在海底之上。由表2可知, 该海管总共有21处悬跨, 其中最大悬跨高度为0.1 m的悬跨段占总段数的 57.1%, 悬跨高度为 0.2 m的占23.8%, 悬跨高度达到1 m以上的只有16号段。悬跨长度20 m以下的悬跨段占总段数的28.6%, 悬跨长度20～40 m的占38.1%, 悬跨长度50 m以上的占19.1%, 即3, 11, 14, 16号段。由实测数据可以看出,悬跨段均位于浅海海域, 且相差不大, 从中筛选出相对危险的悬跨段： 3, 7, 8, 10, 11, 13, 14, 16号段。其中7, 8, 10三段悬跨为一段比较长的悬跨穿过两个沙波形成, 沙坡大小和管道的掩埋深度未知。

2 计算模型

海管管径相对于管跨长度来说是一个极小量。为了便于力学模拟计算, 在数值模型中可以将模型管道看作柔性管, 同时也可以将海底管道的振动假定为梁式弯曲振动。本文采用Euler-Bernoulli梁模型研究带有水泥配重层海管的挠曲变形问题。跨长为L的悬跨海管(如图1所示)弯曲微分方程[3]为：

式中,E为海管的弹性模量;I为海管惯性矩。在海管的双层结构中, 钢管刚度要远大于水泥层的刚度, 因此我们在方程中只考虑钢管刚度[4]。由此可得到海管的惯性矩：

表1 海管设计参数Tab. 1 Parameters of the pipeline

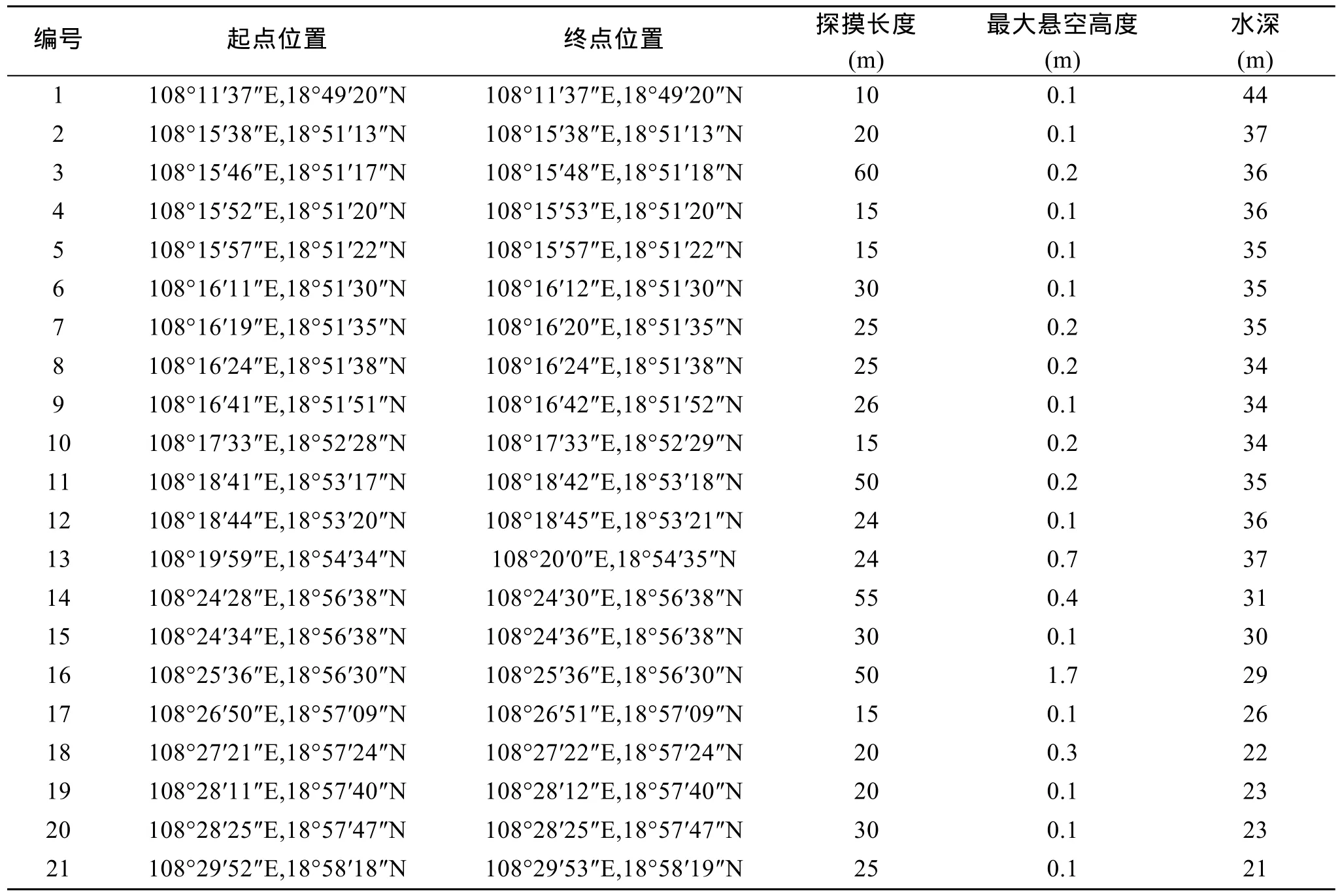
表2 东方1-1气田某段海管悬跨段实际测量数据Tab. 2 Measurements of a spanning pipeline in Dong-Fang 1-1 gas field

式中ts为钢管壁厚,Di为钢管外径, 由于海管两端为弹性约束, 因此可以得出海管的边界条件：

w为海管中点静挠度;sρ为钢管密度;M为海管总质量。钢管的质量与水泥的质量相差不大, 海管质量应为钢管质量和水泥质量之和：

上式中A为海管外截面积;FL为海流对海管的升力, 与外流速度u、外流体密度ρ、海管外径D、悬跨跨长L有关, 公式如下：

式(5)中的CL为升力系数。

图1 两端扭转弹性约束的悬跨海管Fig. 1 An elastically mounted span

由于实测资料中海管的路由都为不稳定的砂质底床, 所以本文的有限元静态模型将重点考虑底床对悬跨段受力的影响。Müller[5]基于势流理论给出的升力解析解与实验差别比较大, 为了得到升力系数沿轴向的分布, 可以基于条带法将海管沿轴向做均匀切片处理, 即对每一截面都用二维的修正势流法得到升力, 进而考察海管升力沿轴向的分布, 将升力加载至有限元模型, 计算得到海管变形沿轴线方向的分布。由修正势流法得到的平底床海管升力系数, 计算结果与实验[6-7]非常接近, 具体推导过程可参看文献[8]。

式中e为海管与底床的间隙(图 1), 根据海管悬跨状况确定两端边界条件。因为海管或是搁在海床上或是穿过沙波, 所以海管两端不能单纯采用固支或者简支的约束条件, 更贴近实际的约束应该是介于固支和简支之间的约束模式[9-10]。本文采用两端带有扭转弹簧的简支约束条件。按实际状态分为两种情况讨论： (1)海管埋入海床中时(如3, 7, 8, 10号段)。悬跨端部受到未悬跨部分的转动约束, 以及海床泥土的转动约束。扭转刚度k取为108Nm/rad。(2)海管搁在海床上时(如11, 13, 14, 16号段)。悬跨端部仅受到未悬跨部分的转动约束, 故其扭转刚度应小于第一种情况。k取为0.2×107Nm/rad。

一般情况下海流速度为 1～2 kn, 即 0.514 4～1.028 9 m/s, 考虑到台风等恶劣天气, 这里将分两种情况讨论海管的疲劳寿命, 一种为一般情况, 海流速度取为0.8 m/s, 另一种为极端海况(台风、风暴潮),底床附近的海流速度取为1.5 m/s 。

确定计算方法之后, 采用ANSYS有限元软件建立起海管模型, 并对模型的静挠度进行求解。不同水深对海管的应力分布以及挠度影响不大, 危险悬跨段主要由悬跨长度和悬空高度决定。下一步对从实测数据中筛选出相对危险的悬跨段： 3, 7, 8, 10, 11,13, 14, 16号进行数值模拟计算, 评价其安全性。

3 计算结果分析

判断海管是否安全有两个标准： (1)刚度失效：若海管的最大位移与海管长度比值小于 0.004, 即则海管处于安全状态; (2)强度失效：若海管承受的最大应力小于许用应力, 即则海管处于安全状态。

由于在平底床的条件下, 钢管更容易发生刚度失效[4], 本文采用第一个标准来判断海管是否安全。首先在考虑一般情况(海底海流速度为 0.8 m/s)的情况下计算海管在自重(空管状态下)和浮力作用下的最大挠度wmax, 看其是否满足的工业标准。确定计算参数如表3、表4所示, 一般将质量附加系数设为常数。

表3 模型钢管计算参数Tab. 3 Parameters of the steel pipe model

表4 模型流场计算参数Tab. 4 Parameters of flow field in the model

海管设计参数中水泥负载厚度为 0.08～0.095 m,本次模拟计算将分别计算这两种负载厚度情况下的海管变形。采用ANSYS有限元软件中的静态分析模块来进行求解[11], 计算的结果按照水泥负载厚度划分。表5为 0.08 m时海管各危险段的静挠度值, 表6为0.095 m时海管各危险段的静挠度值。表中L为海管跨长,h为水深,hs为最大悬空高度,w为最大静挠度。

表5 负载厚度0.08 m时静挠度Tab. 5 Static deflections when the thickness of cement equals 0.08 m

表6 负载厚度0.095 m时静挠度Tab. 6 Static deflections when thickness of cement equals 0.095 m

现实中底床形态有可能是由海水冲刷造成的冲刷坑, 因此对安全隐患较大的 11, 16号段和悬空高度为0.7 m的13号段进行冲刷底床情况下的受力分析, 评价其安全性。在冲刷底床情况下, 升力系数为负[8]。经过计算可得11, 13, 16号段的静挠度如表7所示, 表中h0为原始悬空高度。

表7 0.095 m负载厚度下11, 13, 16号段静挠度Tab. 7 Static deflections of No. 12, 13, and 16 when the thickness equals 0.095 m

由结果可见, 在冲刷底床情况下 11, 16号段海管不能满足的标准, 因此11, 16号段都是不安全的, 尤其是 16号段已经严重超出标准,十分危险。13号段虽然悬空高度较高, 但是由于悬跨跨长比较短, 因此海管中点的静挠度还未到刚度失效的标准。7, 8号段跨长与13号段基本相同, 但悬空高度只有0.2 m, 因此也可以断定7, 8两号段满足的工业标准。

将所得结果按照悬跨长度从小到大绘制出位移走势曲线(图 2), 可以看出随着跨长的增加, 海管的最大位移也在增加。

图2 不同水泥厚度海管最大位移随跨长变化Fig. 2 Span-dependant pipeline displacements at two different thicknesses

将海管的长度固定, 通过改变海流流速可以得到海管中点最大位移随着外流速度的变化规律(图3)。可以看出不同底床形状下, 海管中点最大位移变化规律有显著区别。在平底床条件下海管中点位移随着外流速度的增大而减小, 当外流速度从 0增加到 2.0 m/s时, 海管的中点位移减小了 2.36%, 在冲刷底床条件下, 随着流速的增加, 海管中点最大位移会逐渐变大, 当流速从0增加到2.0 m/s时, 海管的中点位移增加了13.4%。这是因为在平地床条件下,海管升力系数为正, 随着海流流速的增加, 正向升力会FL增大, 从而抵消掉一部分重力; 在冲刷底床条件下, 升力总的效果为负, 所以随着流速的增加,海管中点最大位移变大。

图3 海管最大位移随流速变化Fig. 3 Velocity-dependant displacements of pipeline at two different sea beds

4 结论

本文从实际问题出发, 对东方气田某标段海管的海底悬跨实际情况进行分析, 筛选出一些重点悬跨段, 建立有水动力影响的海管悬跨安全计算的静态模型并且确定了计算参数。通过分析计算结果, 可以得出如下结论： (1)对于筛选出的各重点悬跨段, 3,11, 14, 16号段是不安全的。建议对通过本文计算所得出的不安全号段海管尽快进行加固维护。(2)相对于水泥负载厚度0.08 m, 水泥负载厚度0.095 m时海管更容易发生危险。(3)在平底床情况下, 随着流速的增加, 海管受到的正向升力增加, 其中点位移会减小; 在冲刷底床情况下, 海管会受到负向升力, 其中点最大位移会增加。

[1]Mouselli A H. Offshore pipeline design analysis and methods[M]. United States： Penn Well Books, 1981.

[2]王维. 确定海底埋设输油管线允限冲刷长度的一种实用方法[J]. 西南石油学院学报, 1996, 18(3)： 94-97.

[3]Lin Mian, Cao Yulong, Li Lei, et al. Investigating of a Near-bed Submarine Pipeline in current[C]// the ASME.Proceedings of the ASME 2009 28thInternational Conference on Ocean, Offshore and Arctic Engineering.Honolulu, Hawaii, USA： ASME, 2009： 191-195.

[4]李磊, 曹玉龙, 林缅. 预测近底床悬跨海管的危险跨长 [J]. 中国石油大学学报, 2010, 34(2)： 1-7.

[5]Müller W V. Systeme von doppelquellen in der dbenen strömung [J]. Zeitschrift für Angweandte Mathematik und Mechanik, 1929, 9： 200-213.

[6]Buresti G, Lanciotti A. Mean and fluctuating forces on a circular cylinder in cross-flow near a plane surface [J].Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41(1-3)： 639-650.

[7]Lei C, Cheng L, Kavanagh K. Re-examination of the effect of a plane boundary on force and vortex shedding of a circular cylinder [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 80(3)： 263-286.

[8]李磊. 海流-海管-沙床相互作用及海管安全性研究[D]. 北京： 中国科学院研究生院, 2011.

[9]Magda W. Wave-induced cycle pore-pressure perturbation effects in hydrodynamic uplift force acting on submarine pipeline buried in seabed sediments [J].Coastal Engineering, 2000, 39(2-4)： 243-272.

[10]邢静忠, 柳春图. 考虑海床变形的裸露悬跨海底管道静力分析[J]. 海洋工程, 2007, 25(4)： 21-26.

[11]曹玉龙, 林缅. 基于 ANSYS的近底床悬跨海管建模技术研究[J]. 力学与实践, 2010, 32(6)： 64-68.

Security analysis for the spanning pipelines located in Dong-Fang 1-1 Gas Field

YAO Ping1, FAN Feng-xin2, LI Zhong-yang3, LI Lei3, CAO Yu-long3, LIU Yang3
(1. China National Offshore Oil Corporation, Limited-Zhanjiang Production Department, Zhanjiang 524057, China;2. Key Laboratory of Marine Geology & Environment, Institute of Oceanology, the Chinese Academy of Science,Qingdao 266071, China; 3. Key Laboratory of Environment Mechanics, Institute of Mechanics, the Chinese Academy of Science, Beijing 100190, China)

Feb., 02, 2010

Dong-Fang 1-1 Gas Field; submarine spanning pipelines; assessment analysis; finite element model; sand waves

Submarine pipelines are major instruments for transporting oil and gas. A finite element model was established for the spanning pipelines near a seabed. The variations of pipeline deformation with current velocity was calculated according to the measurement data of Dong-Fang 1-1 Gas Field. The security assessments was analyzed. The dangerous segments of a spanning pipeline were pinpointed. This result will guide the company in preventive measures for dangerous spanning pipelines.

P756.2

A

1000-3096(2011)08-0058-05

2010-02-02;

2010-06-11

中国科学院知识创新工程重要方向项目(KZCX2-YW-212-2); 国家科技部“863”目标导向类项目(2006AA09Z301); 国家基金委自然科学基金项目(40776057)

姚平(1965-), 男, 陕西彬县人, 工程师, 从事海洋工程设施安全保障研究工作,电话： 0759-3902040, E-mail： yaoping@cnooc.com.cn

刘珊珊)