基于兰贝格材料模型管土相互作用对海管横向屈曲的影响
2022-09-02陈政张强
陈 政 张 强
(东北石油大学机械科学与工程学院)
管道因具有连续性、经济性的优点而广泛应用于热力运输[1]、油气运输等行业。 在生产、安装过程中产生的初始缺陷,容易导致管道出现失效和使用寿命缩短的情况[2],因此需要对管道进行相应的研究。 随着油气开发向着海洋进军,用于海底稠油运输的海管也越发受到人们的重视。 海底开采的稠油凝点高、含蜡量较多、粘度较大,因此运输时需要对海管进行加热,加热后的管道容易出现热屈曲现象[3]。 浅海的海管多为半埋或全埋形式,半埋管、全埋管容易出现隆起屈曲;放置在深海的海管多采用裸露敷设,裸露敷设在平坦海床上的海管更容易出现横向屈曲。
在基于小坡角、线弹性假设,以及在没有初始几何缺陷的情况下,HOBBS R E给出了理想直管道横向屈曲临界载荷的计算公式[4]。 陈景皓等对含初始缺陷的海管进行有限元分析,得出初始缺陷的增大会影响海管临界屈曲温度,并对影响管道强度的3种缺陷尺寸进行参数敏感性分析[5]。王泽武等对平铺在刚性海床面上、 含5种缺陷的海管进行横向屈曲非线性数值模拟,得出能够满足含各种通用初始几何缺陷海管抗稳定性设计的表达式,该表达式是基于无量纲分析法开发的临界温升计算表达式,但该表达式并没有关注到管土的相互作用[6]。 LIANG Z等研究了恒定高温高压环境下的海底管道屈曲问题[7]。 利用有限元分析得出,随着温度的升高,管道的应力先增加后减小,文中只考虑了恒定工况下的海管屈曲情况,缺乏对多工况下的海管屈曲分析。 刘羽霄等研究了管土相互作用对海管横向屈曲的影响,通过有限元分析,研究轴向、横向摩擦系数对海底管道横向屈曲的影响,所采用的模型是基于兰贝格(Ramberg-Osgood)材料模型的有限元模型,主要研究的是管土相互作用下海管的临界温差和临界载荷,在分析管土相互作用时,建立的是常温下兰贝格材料本构, 但是由于X65管线钢的弹性模量会随着温度降低,因此对于不同温度下的海管,需要建立单独的兰贝格材料模型[8]。大量学者对高温高压海管横向屈曲进行研究,都验证了在单一工况下,海管横向位移大小随初始缺陷的增大而增大[9~11]。 付长静等综述了海管在波浪作用、海床的管土相互作用下的国内外实验[12]。 王立忠等研究了在进行数值仿真时,海管系统阻尼值和升温速率的确定方法,研究了海管初始几何缺陷和管土相互作用对海管热屈曲动力过程的影响[13]。
笔者以裸露敷设在平坦海床上的海管为研究对象,考虑不同温度的兰贝格材料模型,建立管土相互作用的非线性海管模型, 在多次开工、停工情况下,分析管土相互作用对海管横向屈曲的影响。
1 管土相互作用的海管模型
1.1 非线性海管模型
海管材料为X65管线钢。 海管裸露敷设在水深200 m的海床上, 海床平坦且与海管完全贴合没有间隙,海管进行锚固。 海管外部有一层厚度为5 mm的外部防腐绝缘涂层,在防腐绝缘涂层外部有厚度为55 mm的混凝土。海管外部受到200 m的均布深水压力。海管所处的环境温度为5 ℃,工作时的温度设置为90 ℃[14]。
以上述工况为例,采用ANSYS软件建立对应的有限元模型,将海管离散成PIPE288管道单元。管道外径D=559 mm,壁厚t=19.1 mm,管道长度L=2000 m,管道两端固支,海管模型如图1a、b所示。图1c为海管的局部有限元网格图,文中2 000 m长的海管由管道单元组合而成,每个管道单元长度为2 m,每个管道单元绕圆周划分成24份。
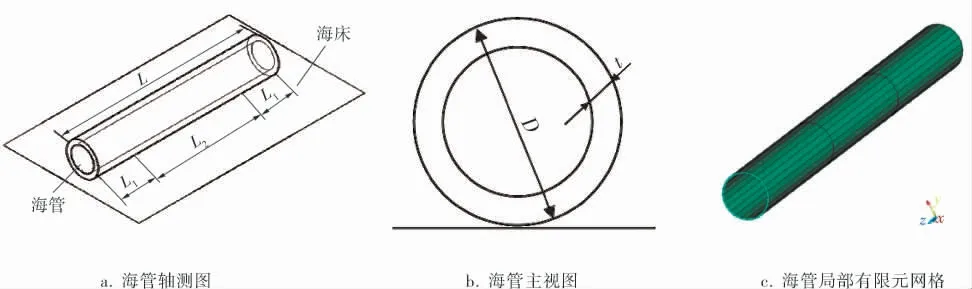
图1 管土相互作用的海管模型


海管两端固支在海床平面上,海管自身受重力G和外部静水压力pex(2.01 MPa)。 在管道960~1 040 m处,施加横向初始扰动力F0=7000 N,给海管一个初始的横向缺陷。 海管与海床涉及到管土相互作用问题, 设置成正交各向异性土壤摩擦。海床表面依附目标单元TARGE170, 海管表面依附接触单元CONTA175。 横向土壤摩擦系数μ1=0.8,轴向土壤摩擦系数μ2=0.5。对海管施加温度载荷T1(90 ℃)和内部工作压力pop(15 MPa),用于模拟海管在海底工作时的状态。 对海管施加温度载荷T2(5 ℃)和内部停工压力pst(1.94 MPa),用于模拟海管在海底停工时的状态。 海管在开工加热时,其边界条件如图2所示(单位:m)。

图2 海管边界条件
为了研究海管在多次开工、停工后的屈曲情况,对海管进行多次加载、冷却。
海管的各工况如下:
a. 工况1,对海管施加初始载荷,产生初始缺陷;
b. 工况2,撤去初始载荷;
c. 工况3,第1次加热,海管施加温度载荷T1=90 ℃和工作压力pop=15 MPa;
d. 工况4,第1次冷却,撤去温度载荷和工作压力, 海管温度降低到5 ℃, 施加停工压力pst=1.94 MPa,用于代替工作压力;
e. 工况5,第2次加热,海管施加温度载荷T1和工作压力pop;
f. 工况6,第2次冷却,海管温度降低到5 ℃,施加停工压力pst;
g. 工况7,第3次加热,海管施加温度载荷T1和工作压力pop;
h. 工况8,第3 次冷却,海管温度降低到5 ℃,施加停工压力pst。
1.2 兰贝格材料模型
海管的材料模型可采用线弹性、 理想弹塑性、兰贝格材料模型[15]。X65管线钢的兰贝格应力σ、应变ε可表示为:


考虑到海管在工作和停工情况下温度不同,需要对不同温度下的海管建立兰贝格材料模型,X65管线钢在不同温度下的应力-应变曲线如图3所示。
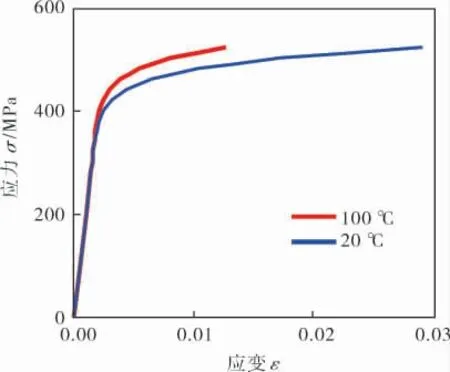
图3 兰贝格应力-应变曲线
1.3 模型的影响因素分析
1.3.1 材料本构模型的影响
为计算分析不同材料模型下的海管屈曲情况,材料本构模型取线弹性、理想弹塑性、兰贝格材料模型,海管最大变形量和受到的最大等效应力曲线如图4所示。 其中,工况7的变形云图如图5a所示,工况8的等效应力云图如图5b所示。

图4 3种材料模型的海管最大变形量和最大等效应力曲线

图5 3种材料模型的海管变形和等效应力云图
结合图4、5可知,基于线弹性材料模型,海管在各工况下的最大变形量和最大等效应力波动较大,工况7的等效应力达2 400 MPa,显然与实际情况不符。 对于理想弹塑性和兰贝格材料模型,在工况1~6的情况下, 海管的变形量和应力均基本重合。 但在工况7下,对比兰贝格和理想弹塑性材料模型的横向位移可见,前者比后者大48%;在工况8下,前者的等效应力比后者小19.6%。 由于理想弹塑性的材料模型做了简化,而兰贝格材料模型更符合真实的应力应变关系,因此,当这两种材料模型的有限元计算结果存在较大误差时,优先选择兰贝格材料模型。
1.3.2 横向约束长度的影响
从图5可知, 横向屈曲主要发生在海管中间段,海管端部及其附近变形量小,为提高计算效率,可对海管端部及其附近施加横向约束。 海管两端设置长度为L1的横向约束, 中间段L2为自由段(图1a)。 海管中间段长度L2分别设置成不同的长度,分析各工况下横向约束长度对海管的最大变形量和等效应力的影响(图6)。
由图6可知,随着中间自由段长度的增加,海管最大变形量与最大等效应力受其影响变小。 当中间自由段长度L2达到740 m后,海管的最大变形量曲线基本可以看作一条水平直线,其最大等效应力曲线也已经收敛,说明中间自由段长度的增加对海管最大变形量已无明显影响,对海管最大等效应力的影响也已可忽略不计。 无任何附加横向约束的情况下,海管各工况下的最大变形量与最大等效应力的数值与L2=740 m时的数值误差在5%以下。 因此,为了简化模型,减少计算量,对2 000 m长的海管左右两端各设置L1=630 m的横向约束,L2=740 m的中间自由段不设置横向约束。

图6 横向约束长度对最大变形量和最大等效应力的影响
2 海管横向屈曲影响分析
2.1 横向摩擦系数的影响
海管在开工加热和停工冷却时,因热载荷和内外压差的影响,会出现热屈曲现象。 当海管裸露布置在海床上时,容易发生横向屈曲。 考虑海管的自重,在屈曲过程中,其与海床之间存在相互作用。 这种管土相互作用关系会在海管发生屈曲时影响其屈曲变形状态。 笔者将海管与海床之间的管土相互作用转化为海管与海床之间存在的摩擦阻力。 该摩擦阻力由横向摩擦阻力和轴向摩擦阻力两部分组成。
为研究横向摩擦系数大小对多次开工、停工情况下海管横向屈曲的影响,笔者分析了横向摩擦系数μ1为0.1~0.9,轴向摩擦系数μ2为0.5的情况下,海管横向位移大小与横向摩擦系数的关系(图7)。

图7 横向摩擦系数对横向屈曲的影响
由图7可知, 经过多次开工加热、 停工冷却后, 当海管与海床之间横向摩擦系数μ1取0.2~0.5时,在加热和冷却过程中,海管膨胀向外屈曲和向内收缩时, 横向摩擦阻力对其阻碍作用较弱,海管的横向位移随着横向摩擦系数的增大而增大; 当海管与海床之间横向摩擦系数较大(μ1取0.5~0.9)时,在加热和冷却过程中,对海管屈曲的约束作用较大,海管横向屈曲受到抑制,其横向位移随横向摩擦系数的增大而减小;当海管与海床之间横向摩擦系数μ1为0.5时,海管的横向位移在1 000 m位置处达到最大,即7.249 m。 图8为横向摩擦系数μ1=0.5,轴向摩擦系数μ2=0.5时,各工况下海管横向位移的曲线。

图8 各工况下横向位移曲线
由图8可见, 由于海管安装时产生的初始缺陷, 在进行第1次开工加热后, 横向位移大幅增加,由1.51 m增加到8.54 m。 在进行多次开工加热和停工冷却后,由于横向摩擦阻力的影响,海管的横向位移有明显的下降趋势。
2.2 轴向摩擦系数的影响
海管与海床之间除了存在横向摩擦系数外,还存在轴向摩擦系数。 在海管开工加热膨胀或停工冷却收缩时,轴向摩擦阻力会阻碍海管的轴向滑移, 使得管道内的轴向应力无法得到释放,从而对海管的横向屈曲造成一定的影响。 为了分析在多次开工、停工情况下,海管轴向摩擦系数对海管横向屈曲的影响,设定海管与海床的横向摩擦系数μ1=0.8,海管与海床之间轴向摩擦系数μ2取0.1~0.9,分析海管横向位移和轴向摩擦系数之间的关系(图9)。

图9 轴向摩擦系数对横向屈曲的影响
从图9可以看出,在进行多次开工、停工后,海管轴向摩擦系数的变动对其横向位移的影响较小。 这一结论与文献[6]所研究的管土相互作用对海管后屈曲影响得到的结论一致。
在文献[6]的研究中,不同轴向摩擦系数对应的管道后屈曲的变形影响不大,轴向摩擦系数μ2在0.5~0.9时, 海管的横向位移随着海管的海管轴向摩擦系数增大而增大。 但笔者考虑了温度对海管材料模型的影响,在多次开工、停工后,海管的横向屈曲随轴向摩擦系数的增大而减小。
3 结论
3.1 将管土相互作用转化为海管与海床之间横向摩擦和轴向摩擦。 在多次开工、停工后,横向摩擦系数在0.2~0.5时,海管的横向屈曲随着横向摩擦系数增大而增大; 横向摩擦系数在0.5~0.9时,海管的横向屈曲随着横向摩擦系数增大而减小。3.2 在多次开工、停工后,轴向摩擦系数的改变对海管横向屈曲影响依然较小。
3.3 在管土相互作用影响下, 多次的开工加热、停工冷却后,海管的横向屈曲能够得到明显的缓解。 说明海管加热技术具备一定的止屈能力。
