卷管铺设的海管曲率模型及残余应力计算

张九菊，段梦兰，胡显伟

(1.北京石油化工学院 机械工程学院，北京 102617;2.复旦大学 力学与工程科学系，上海 200433;3.中国石油大学(北京)海洋油气研究中心，北京 102249;4.中国石油天然气勘探开发公司，北京 100034)

卷管铺设在20 世纪70年代起开始在美国、巴西、欧洲等国家应用，对于小管径管道具有铺设速度快，铺管效率高等特点，在国内，由于市场、技术、铺管船造价等方面的因素，目前还没有卷管铺管船，因此鲜有这方面的研究。

图1 为海管在用卷管铺设的示意图。海管的尺寸通常为4 ～16 英寸时可用于卷管铺设，在上卷及退卷的过程中海管发生了多次弯曲，经历了多次弹塑性变形［1］。Kyriakides 等［2］指出过弯曲会导致海管截面的椭圆化，而椭圆化会降低海管的弯曲能力，甚至使海管发生失稳及局部屈曲。海管在完全卸载时将产生残余应力，残余应力将会对含有缺陷的海管造成局部破坏，甚至整体断裂［3］，影响海管的疲劳寿命［4］。卷管铺设的关键技术包括控制海管的弯曲曲率及矫直等［5］。

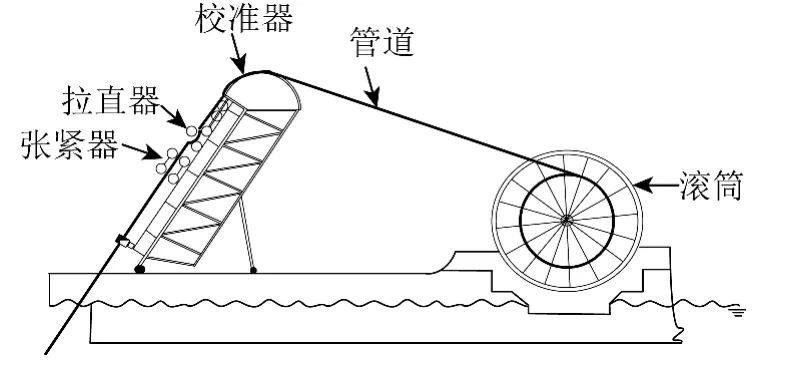
图1 卷管铺设方法简图Fig.1 Sketch of pipeline laying methods

目前为止，巴西对卷管铺设技术的研究较多，巴西里约热内卢联邦大学对海管上卷、退卷过程进行了模拟。Netto 在文献［5］中描述了海管的弯曲模拟过程，用主钢结构模拟滚筒，钢模结构模拟校准器，用液压装置进行驱动，海管的弯曲半径分别由主钢结构和钢模结构的半径决定。并用有限元软件ABAQUS 进行了数值模拟。Douglas 等对海管上卷过程也进行了研究，不同的是，文献［6］针对不同的管材，不同的弯曲半径，用“四点弯曲法”仿真模拟，该试验主要通过控制中间两点的位移来实现管道的弯曲与拉直。文献［7］提出了管道的名义应变近似为管道的弯曲半径与滚筒半径的比值，并画出了卷管铺设过程中在驱动载荷的作用下的应力-应变响应曲线，且规定管道塑性应变不能超过3%［8-10］。残余应力改变了管道的材料力学性质，对管道的极限强度及疲劳性质有一定的影响［8，11-12］。Eikrem 等［13］用试验对含有缺陷的管道施加弯矩及反向弯矩，试验结果表明残余应力加大了裂纹尖端应力。到目前为止，对卷管铺设的研究可供参考的资料较少，学者们对海管弯曲曲率及残余应力的研究大多是只针对卷管上卷时进行了初步的分析研究，而对海管复杂的循环受力过程的深入研究目前尚少见。为此，将针对卷管铺设过程中海管的上卷、完全卸载、退卷(反向加载)、再次卸载等各个步骤中的弯曲曲率及残余应力的力学模型分别进行研究，并考虑当海管的截面从外向内逐渐屈服时，寻找海管截面上残余应力的分布规律，并分析影响海管弯曲曲率及残余应力变化的参数。

1 卷管铺设的海管弯曲曲率模型

海管曲率通常以海管发生弹性变形为条件，由几何关系得到曲率半径与应力的关系式，使得应力强度小于海管的许用应力，从而得到海管的曲率设计值。而实际上，在卷管铺设中海管不可避免地将发生弹塑性变形，在反复加载的情况下，简单的线弹性已不能描述海管的弯曲曲率变化。

1.1 海管弯曲曲率模型简化的基本假设

为使复杂的问题研究方便且与实际工程接近，选取纯弯曲的加载方式，所研究的问题可视为受纯弯曲的梁的弹塑性力学问题，对加载后的梁进行卸载过程分析，求其残余曲率解析解，及再次加载后梁的残余曲率。在研究海管曲率模型时采用如下假设:

1)材料的应力、应变关系采用普朗特简化曲线;

2)把滚筒、校准器看作刚性体，海管材料可承受大变形;

3)海管上卷时施加的弯矩超过了弹性极限弯矩，海管材料发生了弹塑形变形;

4)海管卸载时，弯矩改变量和曲率改变量之间服从弹性关系;

5)海管截面在变形之后仍然保持平面且近似为圆截面［14］。

1.2 海管上卷的曲率模型

海管上卷缠绕到滚筒上的截面如图2 所示。

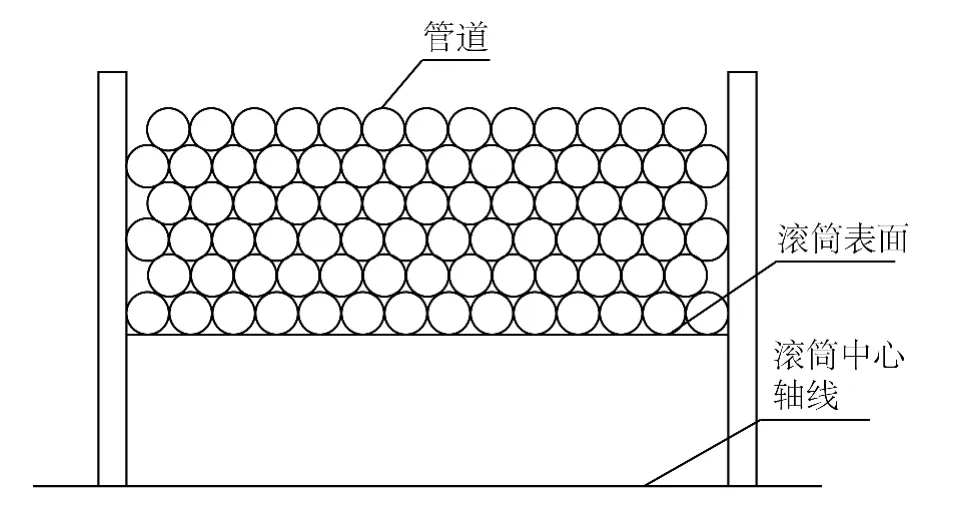
图2 管道缠绕滚筒截面示意Fig.2 The section of pipe reel-on

运用卷管铺设方法时海管上产生的最大应变:

式中:D 为海管直径，R 为滚筒半径。

缠绕在滚筒上最内层海管的弯曲曲率:

式中:K*为海管弯曲曲率。

缠绕在滚筒上外1 层海管的弯曲曲率:

依次类推，缠绕在滚筒上外n 层海管的弯曲曲率:

由于最内层海管所受应力最大，最容易失效，所以仅对最危险情况，即最内层海管的弯曲曲率讨论。

1.3 海管完全卸载后曲率模型

从滚筒上卸载时，弯矩改变量和海管的曲率改变量之间服从弹性规律，即，弯矩改变量ΔM 和曲率改变量ΔK 之间为线性关系，即:

式中:ΔM 为弯矩改变量，ΔK 为曲率改变量，Ke为海管弹性极限曲率，Me为海管弹性极限弯矩。

当弯矩M*完全卸载到零，即:

式中:M*为上卷加载弯矩。

由式(6)和式(5)得到:

由式(7)得到:

进一步推导式(8)得:

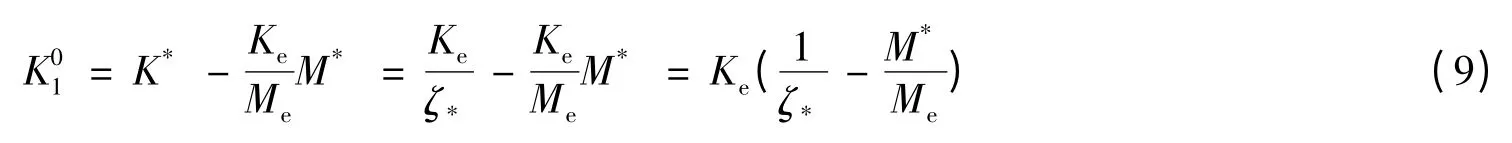
1.4 海管退卷曲率模型

海管在卷管铺设中的力学模型简化为图3 所示，曲率变化如图4 所示。

1→2:海管上卷到滚筒上的过程，曲率变化对应图4 中的从O 到A 的过程。

2→1:海管卸载的过程，相应的曲率变化为图4 中的从A 到B 的过程。

1→3:海管退卷过程，对海管施加了反向弯矩，海管缠绕到了校准器上，相应的曲率变化为图4 中的从B到C 的过程。

3→1:海管再次卸载，相应的曲率变化为图4 中的从C 到D 的过程。

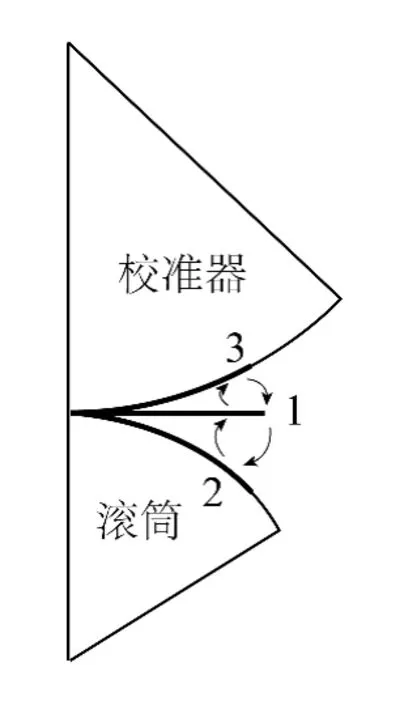
图3 海管力学模型简化Fig.3 Submarine pipe mechanical model

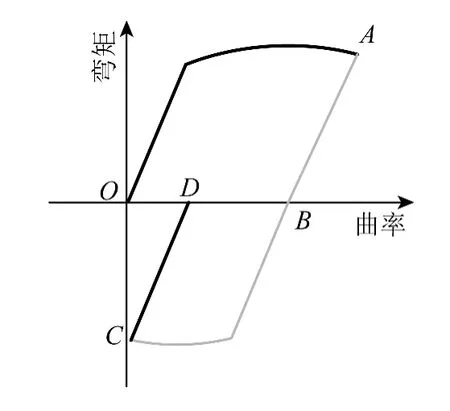
图4 海管的弯矩与曲率关系Fig.4 Relation between bending moment and curvature of pipe

反向加载产生的残余弯曲曲率求解方法同1.3 节，本节不再赘述。退卷时产生的残余弯曲曲率与上卷时产生的残余弯曲曲率方向相反，两者可相互抵消一部分。

式中:K0为最终的残余弯曲曲率为退卷时产生的残余弯曲曲率。

式(10)为海管上卷与退卷的残余曲率累加值，是判断海管失效的重要判据。除此之外，海管上的残余应力以及残余应力的累加值是判断海管失效的另一重要判据。

2 卷管铺设下海管残余应力的计算

在对海管铺设进行设计时通常认为只发生弹性变形，没有残余应力产生，忽略残余应力对海管铺设的作用，只强调应力对海管产生的影响。实际上残余应力累加到一定程度同样会导致海管失效。

2.1 残余应力力学模型的建立

1)力学模型描述

图5 为海管上卷退卷的应力应变关系曲线;图6 为海管截面的纵向截面图。设从中性轴到距中性轴为x0处是弹性变形部分，在x0以外部分为塑性变形部分。当海管完全卸载时，从中性轴到x0的部分沿着oa 变形，而应变量为εf的塑性变形部分则沿着bd 线进行弹性回复变形。沿oa 变形的部分，在其应变量回复到零时，其应力亦回复到零。而沿bd 线变形回复的部分，应力为零时还残留有应变εe，因此，欲使其应变恢复到零，应力值必须沿弹性线bd 变化到应力为负值的一侧。

图5 海管上卷、退卷的应力-应变曲线Fig.5 Relation between stress and strain during reel-in and reel-off

图6 海管纵向截面示意Fig.6 Longitudinal sectional view of pipe

2)海管的应力-应变本构关系

弹性阶段:

式中:σ 为海管截面上的应力，E 为海管弹性模量，ε 为海管弹性应变。

塑性阶段:

式中:σs为海管屈服应力。

3)屈服准则

初始屈服条件:

后继屈服条件与初始屈服条件相同。

4)加载、卸载判别准则

式中:dσij为施加的应力增量，f 为海管屈服面函数。

5)海管退卷后应力增量与应变增量关系

海管在上卷、退卷时均发生了塑性变形，塑性应变增量与应力及应力增量之间的关系:

式中:d{ε}p为海管塑性应变增量，dλ 为非负的尺度参数。

设海管在一个无限小的应力增量dσ 作用下，产生了弹性应变增量和塑性应变增量，关系式为

式中:［D］e为弹性常数，d{ε}e为海管塑性应变增量，d{σ}为应力增量。

由式(15)和式(16)得海管退卷后应力增量与应变增量关系:

2.2 卷管铺设中残余应力的求解

1)海管上卷后再卸载残余应力的计算

海管在上卷过程中发生了弹塑性变形，上卷时施加在海管上的弯矩大于海管开始屈服时所对应的弯矩，随着M 值的增大，塑性区将由海管截面的最外层向内逐渐扩展(如图7(a)，(b)所示)。

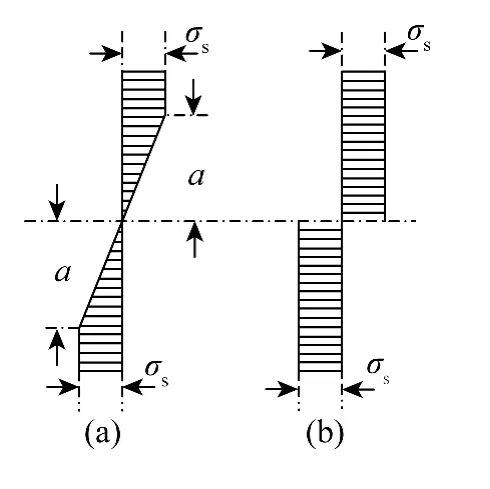
图7 海管截面应力分布Fig.7 Stress distribution of pipe section

图8 卷管铺设时应力与应变关系曲线Fig.8 Relation between stress and strain in reel-lay

海管截面屈服位置的不同对应海管的弯曲曲率不同，而弯曲曲率是由施加在海管上的弯矩产生，文献［15］中对弯矩表达式的推导做了详细的论述。

海管截面应力表达式:

式中:y 为海管截面上所要研究的位置与中性轴的距离。

卸载时，海管截面应力改变量与曲率改变量之间符合弹性关系:

式中:Δσ 为海管截面应力改变量，J 为海管截面的惯性矩。

海管截面残余应力分布是式(18)和式(19)的叠加，残余应力表达式:

2)海管退卷残余应变分析

海管在上卷、退卷过程中的应力-应变关系曲线为如图8 所示。

海管上产生的残余应变为:

式中:ε0为海管上卷、退卷的最终残余应变为上卷后产生的残余应变为海管退卷后产生的残余应变。

通常情况下，反向加载能使海管的残余应变大大减小，却无法完全被消除，这与加载方式，加载设备精密度有关。

上述残余应力、残余应变的求解公式是判断海管是否失效的主要判据。

3 控制卷管铺设的主要参数及其规律

曲率及残余应力是海管在进行卷管铺设时要严格监控的两个物理量，研究影响海管曲率及残余应力变化的关键参数，通过控制基础参数来提高卷管铺设系统的可靠性。

以海管内径与外径之比分别为0.714、0.8、0.9、0.98［16］为例对曲率和残余应力以及与之紧密相关的参数进行分析。

3.1 曲率

上卷时缠绕在滚筒上的最内层海管的曲率可由式(2)计算得到。

一般滚筒直径为［17］:

由式(2)和式(23)可得:

说明K*与R 成反比例关系。

［7-8］，海管的应变不超过3%，即:

适宜于卷管铺设的海管管径取值范围为4 ～16 英寸［17］，由式(1)和式(25)以及管径的范围得出滚筒的直径范围:

由式(24)得出海管的弯曲曲率:

表1 为目前海管在卷管铺设中所用过的滚筒半径与弯曲曲率［17］。图9 为文中所设计的滚筒半径与弯曲曲率的关系。

表1 滚筒设计半径与海管弯曲曲率Tab.1 Hub radius and pipe curvature

从图9 可看出:

1)目前已经应用的滚筒半径及海管的弯曲曲率与本文所设计的滚筒半径及海管的弯曲曲率基本保持一致。

2)K*＜0.135 3 m－1为本文所推荐的海管的最优弯曲曲率设计值。

3.2 曲率比

曲率比是上卷时的曲率与弹性极限曲率的比值，曲率比为海管弯矩比与管径比的函数。

引入无量纲弯矩和无量纲曲率。

图9 滚筒半径与卷管弯曲曲率关系Fig.9 Relation between hub radius and pipe curvature

式中:m 为弯矩比，δ 为弯曲曲率比。

由2.2 节可知海管截面屈服位置不同，加载弯矩亦不同，即弯曲曲率比不同，弯矩比亦不同。对文献［15］中的弯矩公式进一步推导得:

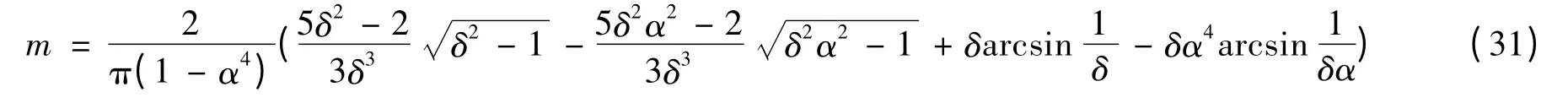
综合卷管铺设实例所用海管的α 值取值范围为0.714 ～0.98［16］。

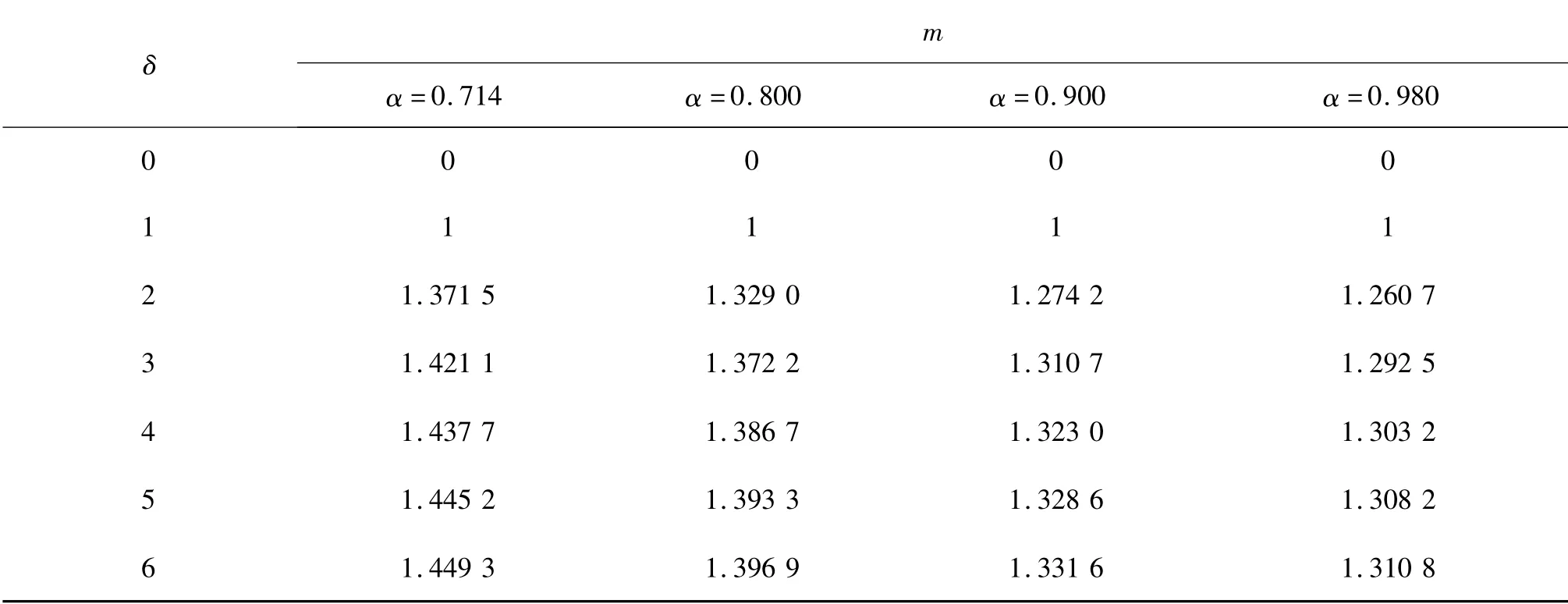
表2 α 取值不同，m 和δ 的对应关系Tab.2 Relation between m and δ when α is different

针对α 取值不同，得到m 和δ 关系，如图10 所示。

图10 α 取值不同，m 和δ 关系Fig.10 Relation between m and δ when α is different

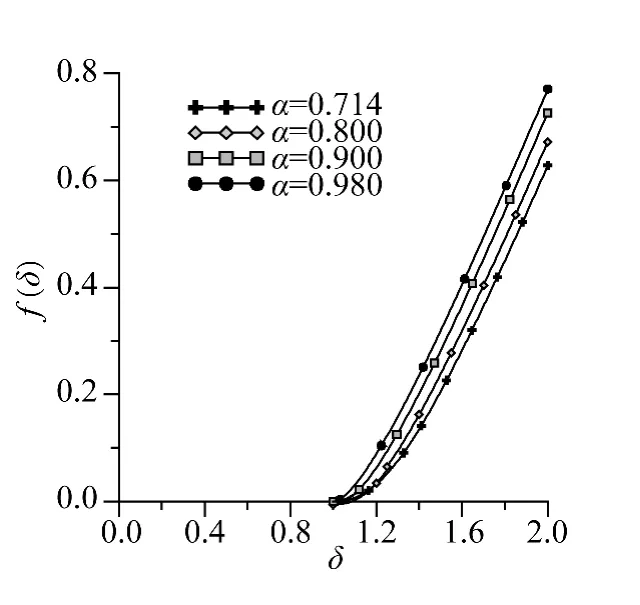
图11 δ 与f(δ)关系Fig.11 Relation between δ and f(δ)

从图10 中我们可以看出，海管进入塑形区后:

1)当δ 取值相同时，α 值越大，m 值越小，即，对于曲率比相同的两根海管，管径比越大，加载弯矩比越小;

2)当α 取值相同时，δ 值越大，m 值越大，即，对于同一海管，曲率比越大，弯矩比也越大。

3.3 残余曲率比

残余曲率比是残余曲率与弹性极限曲率的比值。对于弹性极限曲率相同的海管，残余曲率比的变化规律可以反应残余曲率的变化规律。

由式(8)得到:

设:

以3.2 节中的数据为例计算并画图，如图11 所示。

从图11 中可看出，海管进入塑性区后，对于管径比相同的海管，曲率比越大，则残余弯曲曲率比越大;对于曲率比相同的海管，管径比越大，则残余曲率比也越大。

3.4 残余应力

1)对于残余应力表达式中的线性部分，设:

结合3.2 节中的数据画出F(δ)的图，如图12 所示。

①当0 ＜δ ＜1 时，海管处在弹性阶段，F(δ)=0 海管上的残余应力为零;

②当δ ＞1 时，从图中可以看出F(δ)＞0，海管上有残余应力，且残余应力与海管上原来的应力方向相同;

设:得到g(δ)与δ 的关系曲线如图13 所示。

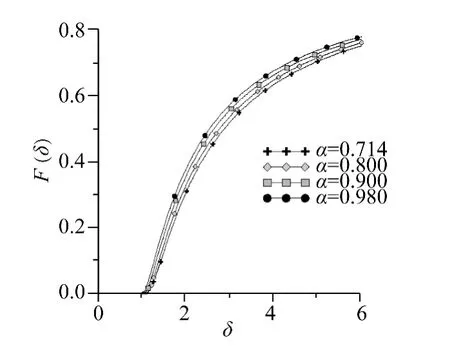
图12 δ 与F(δ)关系Fig.12 Relation between δ and F(δ)

图13 δ 与g(δ)关系Fig.13 Relation between δ and g(δ)

从图13 中可以看出:

①当0 ＜δ ＜1 时，海管处在弹性阶段，g(δ)=0，海管上的残余应力为零;

②当δ ＞1 时，g(δ)＜0，即σ0＜0，海管上的残余应力改变了符号，与原来的应力方向相反;

③对于曲率比相同的海管，管径比越大，残余应力的绝对值越小;

④对于管径比相同的海管，曲率比越大，残余应力的绝对值也越大。

4 结 语

在一定的假设条件下，对海管的上卷、退卷两个过程进行了曲率及残余应力的研究，建立了海管在上卷时的曲率模型、完全卸载时的曲率模型以及退卷时的曲率模型，并得到了各自的解析解，为卷管铺设的参数设计及工程实践提供了理论基础。基本的结论和建议如下:

1)K*＜0.135 3 m－1为文中所推荐的海管的最优弯曲曲率设计值，并通过实例进行了验证，结果表明本文所设计的结果与实例结果基本吻合。

2)上卷时海管的曲率比由海管的管径比和弯矩比决定。对于曲率比相同的两根海管，管径比越大，加载弯矩比越小。对于同一海管，曲率比越大，弯矩比也越大。

3)海管完全卸载后残余曲率比是管径比和曲率比的函数。对于管径比相同的海管，曲率比越大，则残余弯曲曲率比越大;对于曲率比相同的海管，管径比越大，则残余曲率比也越大。

4)海管完全卸载后残余应力的弹性部分与与海管上原来的应力方向相同。且当时，海管的残余应力最大。

5)海管完全卸载后残余应力的塑性部分与海管上原来的应力方向相反。对于曲率比相同的海管，管径比越大，残余应力的绝对值越小。对于管径比相同的海管，曲率比越大，残余应力的绝对值也越大。

6)文中所得的数据关系是基于一定的假定获得的，在实际应用中应该考虑海管的椭圆度，焊接缺陷等影响，因此可能需要更保守的曲率要求。

参考文献:

［1］SZCZOTKA M.Pipe laying simulation with an active reel drive［J］.Ocean Engineering，2010，37:539-548.

［2］KYRIAKIDES S，OK A，CORONA E.Localization and propagation of curvature under pure bending in steel tubes with Luders bands［J］.International Journal of Solids and Structures，2008，45:3074-3087.

［3］NOURPANAH N，TAHERI F.Development of a reference strain approach for assessment of fracture response of reeled pipelines［J］.Engineering Fracture Mechanics，2010.77:2337-2353.

［4］邢永明，雷振坤，戴福隆，等.利用材料拉压异性无损检测残余应力的新方法［J］.力学学报，2001，33(2):264-269.(XING Yongmin，LEI Zhenkun，DAI Fulong，et al.A novel method for nondestructive measurement of residual stress making use of different material properties in tension and compression［J］.Chinese Journal of Theoretical and Applied Mechanics，2001，33(2):264-269.(in Chinese))

［5］NETTO T A，LOURENCO M I，BOTTO A.Fatigue performance of pre－strained pipes with girth weld defects:full－scale experiments and analyses［J］.International Journal of Fatigue，2008，30:767－778.

［6］RODRIGUEZ D E，OCHOA O O.Flexural response of spoolable composite tubulars:an integrated experimental and computational assessment［J］.Composites Science and Technology，2004，64:2075－2088.

［7］DNV－RP－F108，Fracture control for pipeline installation methods introducing cyclic plastic strain［S］.Norway:Det Norske Veritas，2006.

［8］DNV－OS－F101，Submarine pipeline systems［S］.Norway:Det Norske Veritas，2007.

［9］ØSTBY E，JAYADEVAN K R，THAULOW C.Fracture response of pipelines subject to large plastic deformation under bending［J］.International Journal of Pressure Vessels and Piping，2005，82:201－215.

［10］DAKE Y，SRIDHAR I，XIAO Z，et al.Fracture capacity of girth welded pipelines with 3D surface cracks subjected to biaxial loading conditions［J］.International Journal of Pressure Vessels and Piping，2012，92:115－126.

［11］EIKREM P A，ZHANG Z L，NYHUS B.Effect of plastic prestrain on the crack tip constraint of pipeline steels［J］International Journal of Pressure Vessels and Piping，2007，84:708－715.

［12］NETTO T A，BOTTO A，LOURENCO M I.Fatigue performance of pre－strained pipes with girth weld defects:local deformation mechanisms under bending［J］.International Journal of Fatigue，2008，30:1080－1091.

［13］EIKREM P A，ZHANG Z L，ΦSTBY Z，et al.Numerical study on the effect of prestrain history on ductile fracture resistance by using the complete Gurson model［J］.Engineering Fracture Mechanics，2008，75:4568－4582.

［14］HANSEN V，SODANL N.Reeling and J－lay installation of SCR’s on Roncador field［C］// Proceeding of OTC.2001:1－8.

［15］张九菊，段梦兰.管线上卷极限弯矩分析［J］.应用力学学报，2012，29(3):321－324.(ZHANG Jiuju，DUAN Menglan.The limit moment analysis of reeling－on pipeline［J］.Chinese Journal of Applied Mechanics，2012，29(3):321－324.(in Chinese))

［16］ESTEFEN S F.Collapse behaviour of intact and damaged deepwater pipelines and the influence of the reeling method of installation［J］.Journal of Constructional Steel Research，1999，50:99－114.

［17］KYRIAKIDES S，CORONA E.Mechanics of offshore pipeline［R］.Chennai:Charon Tec.Ltd.，India，2007:43－48.