完备剩余幂集格的经典同构对象*

方进明,韩 慧

(中国海洋大学数学科学学院,山东青岛266100)

0 引 言

模糊集又称L-集,是Zadeh在1965年创立的模糊集合论中提出的。设论域X是不空集合,L是隶属度值格,X上的L-集全体记作LX,称之为X的L-幂集格。特别地,当L={0,1}时,LX等同于X的幂集。此后,国内外学者对模糊集合与经典集合之间的联系进行了广泛的研究,其中表现定理是建立这种联系的主要形式,其本质都是寻找L-幂集格的经典同构对象。学者罗承忠[1]最早提出集合套的概念,并以此为工具建立了模糊集的表现定理。随后文献[2-4]等又分别研究了基于不同形式集合套上的模糊集表现定理。文献[5-6]在值格L仅为完备格的条件下,用不同工具研究了L-集表现定理。近年来,若干相关的工作在不断进展中,其中文献[7]是较新的研究成果之一。为使L-集能在多值逻辑环境下描述问题,现在文献中多以完备剩余格作为L-集的隶属度值格,如文献[4]等,本文简称此时的L-幂集格LX为完备剩余幂集格。事实上,可以证明此时LX关于从L上诱导的张量积和蕴涵运算的确是构成完备剩余格。完备剩余幂集格作为完备剩余格,其上有适合进行多值逻辑推理的张量积和蕴涵运算。因此,完备剩余幂集格较文献[5-6]中涉及的完备幂集格的代数结构要复杂。基于此,寻找完备剩余幂集格的经典同构对象是有待研究的问题。

本文的目的是在现有工作的基础上,给出完备剩余幂集格的经典同构对象,从而建立完备剩余格环境下的L-集表现定理。

1 预备知识

文中L记完备格,0和1分别记L中的最小元和最大元,X是非空集合。映射A:X→L称为模糊集或L-集,其全体记为LX,用0X,1X表示LX中的最小元与最大元。X的子集的全体记作P(X),本文不区分X的子集及其对应的特征函数。对任意a∈L和A∈LX,记A的截集为Aa={x∈X|A(x)≥a},L-集(a∧A):X→L和(a∨A):X→L的意义分别是对任意x∈X,(a∧A)(x)=a∧A(x)和(a∨A)(x)=a∨A(x)。

一般地,当L是完备格时,LX也是完备格。下面给出L为完备格时的一些预备结论,其中多数在文献中已见。

定理1[2-3](L-集分解定理)设X是非空集,L是完备格,则对每个

推论1 若A,B∈LX,则A=BΖΠa∈L,Aa=Ba。

命题1 若{At}t∈TΑLX,则对任意a∈L,有

定义1[4]设映射H:L→P(X)满足:

设H,G∈HL(X),定义HL(X)中的偏序关系关于此偏序关系,HL(X)有最小元其中意义如下:设HL(X)中的下、上确界意义如下:

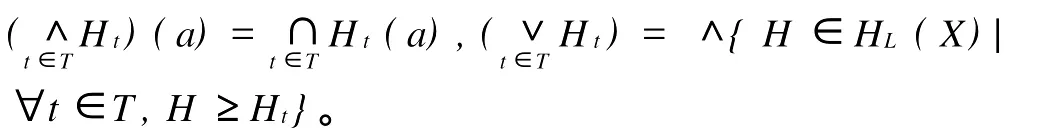
根据上面的定义,可证偏序集(HL(X),≤)是完备格,即下面的命题2。

命题2 设X是非空集,L是完备格,则(HL(X),≤)是完备格。

命题3 设A∈LX,H∈HL(X)。若对任意x∈X,A(x)=∨a∈L(a∧H(a)(x)),其中H(a)(x)理解为H(a)的特征函数,则对任意a∈L,有Aa=H(a)。

定义2[4]设(L,≤)是完备格。若L上有二元运算和→满足:

2 HL(X)中的张量积与蕴涵运算

本节在隶属度值格L为完备剩余格的条件下,首先由LX上的张量积与蕴涵运算相应地定义HL(X)中的运算,然后在预备知识部分已得结论的基础上证明HL(X)关于定义的张量积与蕴涵运算构成完备剩余格。

一般地,当L是完备剩余格时,LX从L中点态地诱导出格运算“(A→B)(x)=A(x)→B(x),其中A,B∈LX,x∈X。不难证明LX关于和→是完备剩余格。

相应地,下面在HL(X)上定义张量积和蕴涵运算→。然后,证明HL(X)关于运算和→是完备剩余格。

定义3 设H∈HL(X)。定义L-集θH:X→L为:并称θH是由H诱导的L-集。

运用由集合套诱导L-集的概念,HL(X)上的张量积运算及蕴涵运算可以自然的定义。为此,先介绍2个引理解决定义的合理性。

引理1 设H,G∈HL(X)。定义映射P(X)如下:

(LH1)对a,b∈L,若a≤b,则

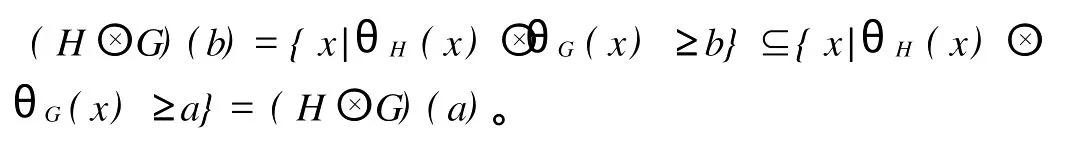
引理2 设H,G∈HL(X)。定义映射H→G:L→P(X)如下:

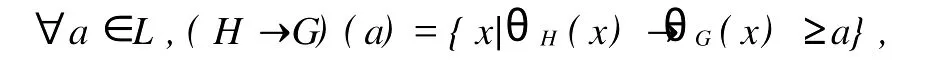
则H→G∈HL(X),即H→G是L-集合套。证明 用引理1的方法证明。

基于上述HL(X)中定义的运算,可以得到下面的重要定理。

定理2 HL(X)关于构成完备剩余格。

证明 (1)首先,由命题2可知,(HL(X),≤)是完备格,其最大元记作意义如下:(2)证是交换的单位半群,即(R1)成立。

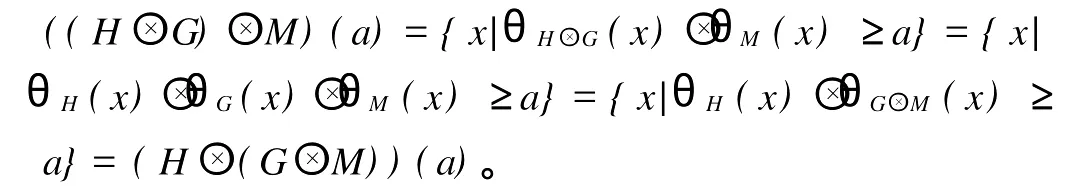
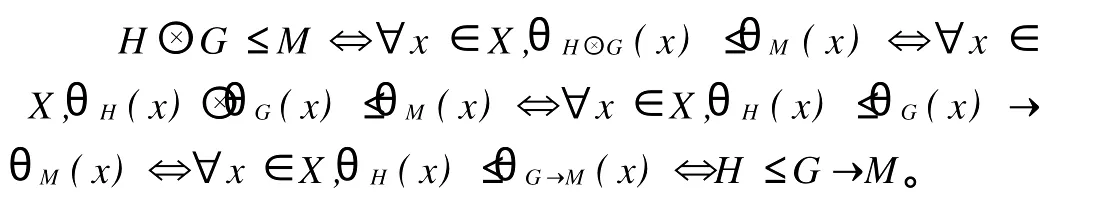
最后,根据上述(1)-(3)及定义2得(HL(X),≤)关于运算和→是完备剩余格。证毕。

3 完备剩余幂集格的经典同构对象

本节将在上节的基础上界定完备剩余幂集格的经典同构对象,并建立完备剩余格环境下的L-集表现定理。首先,给出如下引理。

引理3 设M,L是完备剩余格。若f:M→L是完备格同构,则f保持张量积运算当且仅当f保持蕴涵运算。证明 必要性:设f保持张量积运算。首先需指出,

在f为完备格同构时,易证f-1也是保持张量积运算的。为证f保持蕴涵运算,任取x,y∈M,由M是完备剩余格知,上式两边同时作用f得,,从而f(y)。另一方面,对两边同时作用f-1得,从而f-1(f(x)→f(y))≤x→y。两边同时再作用f得,f(x)→f(y)≤f(x→y)。综上知,f(x→y)=f(x)→f(y)。

充分性:设f保持蕴涵运算。首先,在f是完备格同构时,易证f-1也保持蕴涵运算。为证f保持张量积运算,任取x,y∈M,由M是完备剩余格知,上式两边同时作用f得y),从而。另一方面,对两边同时作用f-1得,y≤x→,从而。两边同时再作用f得综上知,证毕。

下面的同构定理3给出了完备剩余幂集格的经典同构对象。

证明 定义映射f:HL(X)→LX使得对任意H∈HL(X),f(H)=∨a∈L(a∧H(a))。

(1)证f是一一映射。事实上,若f(H1)=f(H2),则由推论1知,对任意a∈L,有(f(H1))a=(f(H2))a。进而由命题3可得,对任意a∈L,H1(a)=H2(a),从而H1=H2。因此f为单射。又对任意A∈LX,定义映射H:L→P(X)使得对任意a∈L,H(a)=Aa,则H∈HL(X)。由定理1知f(H)=∨a∈L(a∧H(a))=∨a∈L(a∧Aa)=A,因此f是满射。

任取x∈X及H,G∈HL(X),下列等式成立:因此,由x的任意性知f,即f保持张量积运算。

由引理3知f也保持蕴涵运算。综合(1)和(2)可得,f为与之间的同构映射,从而证毕。

因此,在L-集合的隶属度值格是完备剩余格的条件下,定理3肯定了L-幂集格LX的经典同构对象是HL(X),此即完备剩余格环境下L-集合的表现定理。

4 结语

完备剩余格是适合多值推理要求的隶属度值格。L-集合表现定理的研究是格值集合理论的重要内容,但此前的研究都不要求L-集合的隶属度值格是完备剩余格。出于格值集合在表示概念时应该适合多值推理的考虑,当前文献中的L-集合多要求隶属度值格是完备剩余格。本文结果表明在完备剩余格的环境下,L-幂集不但是完备剩余格,而且可以证明L-集合的经典对象L-集合套在合理的运算下也构成完备剩余格,而且二者仍然是完备剩余格同构,此即本文的主要结果定理3。L-集合套理论是L-集合理论的层次分析或水平分析的主要工具。因此本文的理论结果进一步肯定在完备剩余格环境下,使用L-集合表示概念时,L-集合套仍然可以对L-集合所表示的概念给出层次分析或水平分析。

[1] 罗承忠.Fuzzy集与集合套[J].模糊数学,1983,3(4):113-126.

[2] 张文修.模糊数学基础[M].西安:西安交通大学出版社,1984.

[3] 史福贵.Lβ集合套与Lα集合套理论及应用[J].模糊系统与数学,1995,9(4):65-72.

[4] Belohlavek R.Fuzzy relational system s:foundations and p rincip les[M].New York:Kluw er Academic/Plenum Publishers,2002.

[5] 熊凤兰.完备格上的表现定理及应用[J].青岛海洋大学学报,1998,28(2):339-344.

[6] 方进明,韩元良.一种新的L-集表现定理[J].中国海洋大学学报:自然科学版,2008,38(6):1025-1028.

[7] Gorjanac-Ranitovic M,Tepavcevic A.General form of lattice-valued fuzzy sets under the cut worthy approach[J].Fuzzy Sets and System s,2007,158(11):1213-1216.