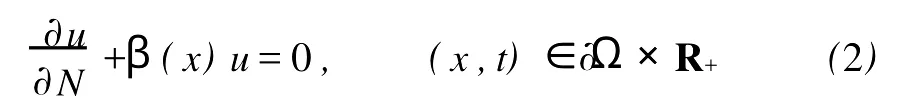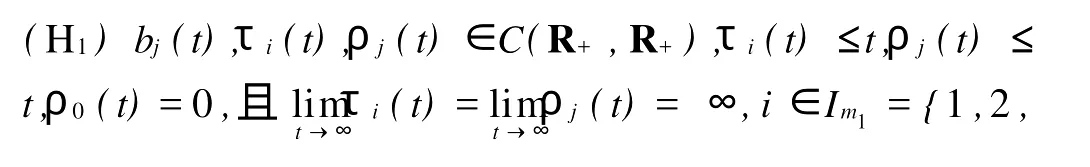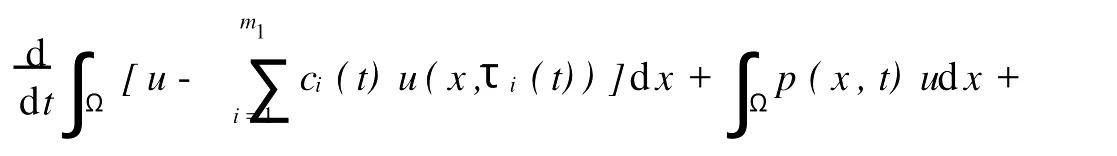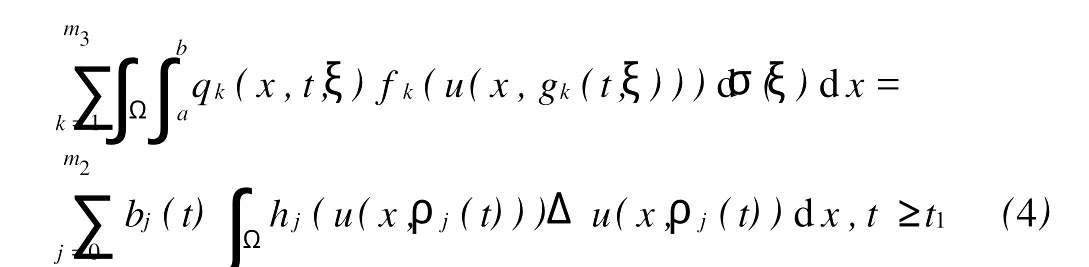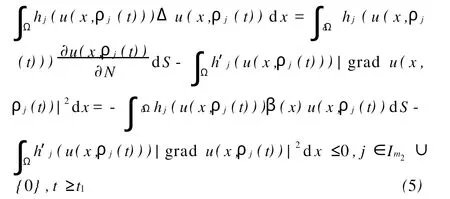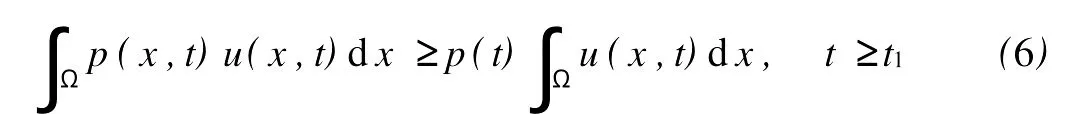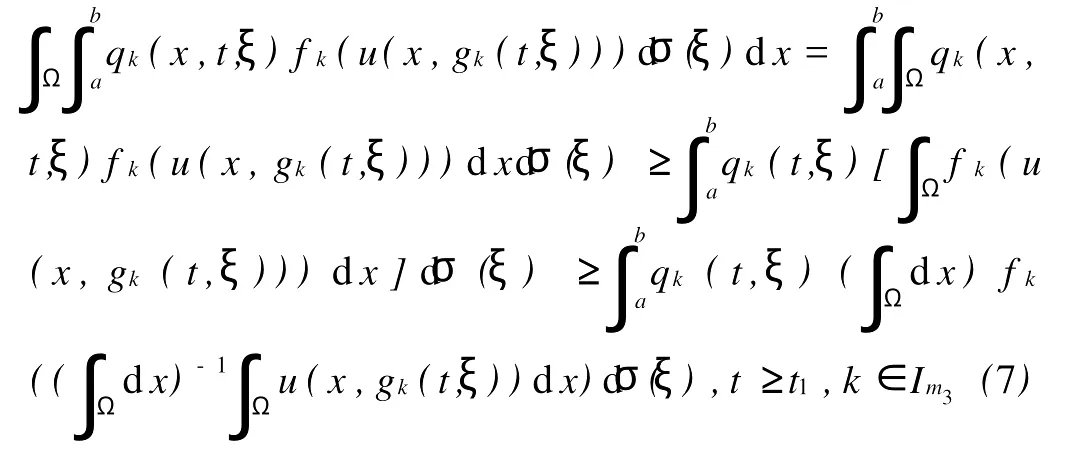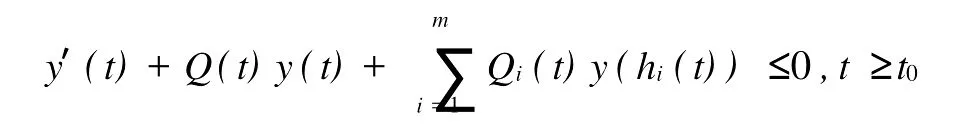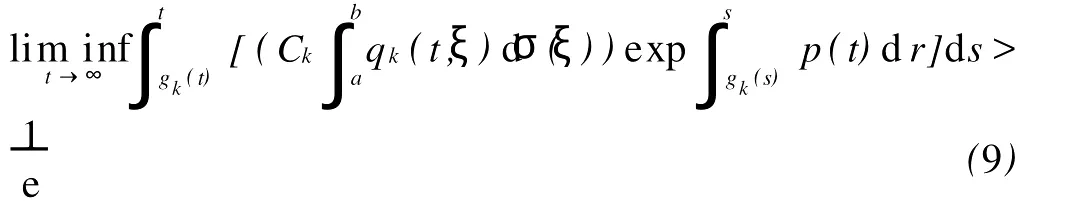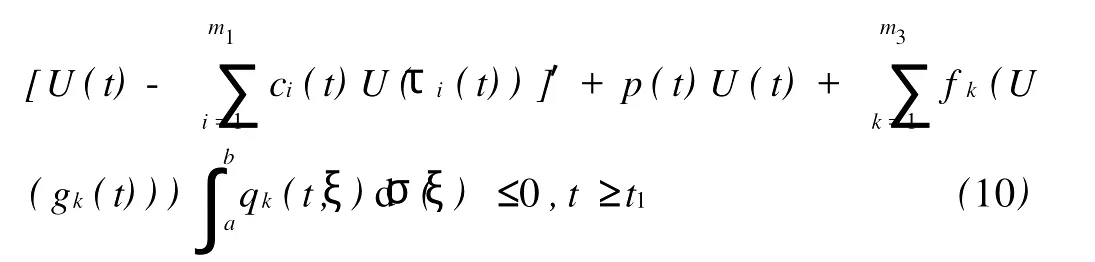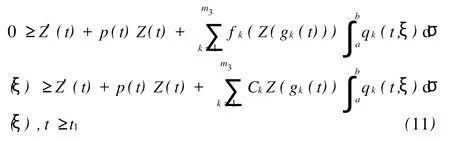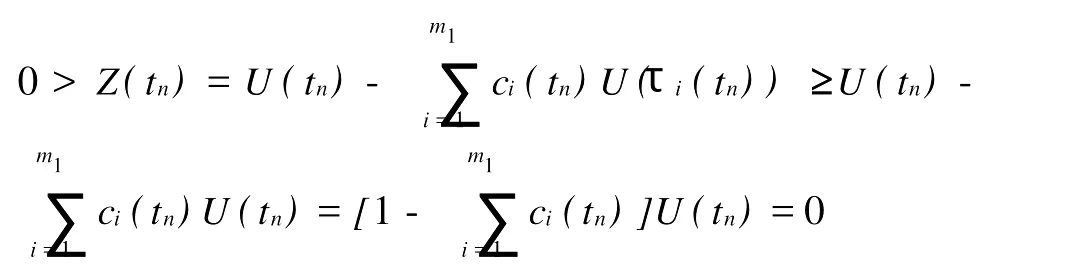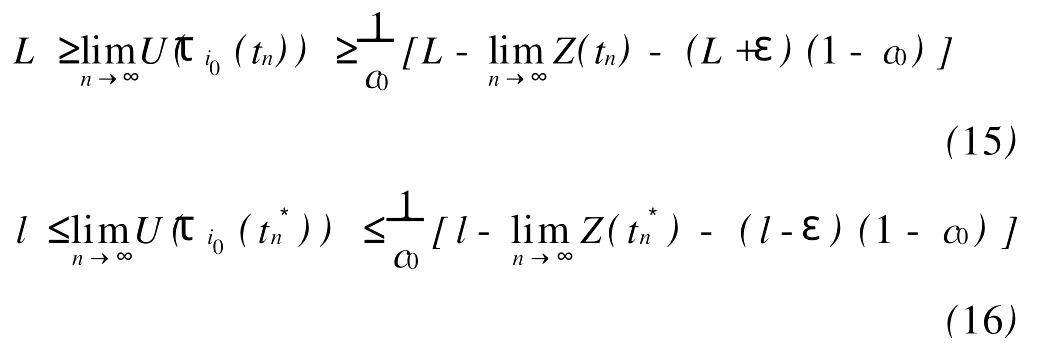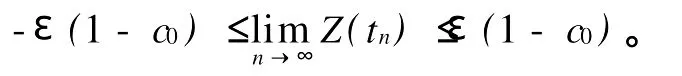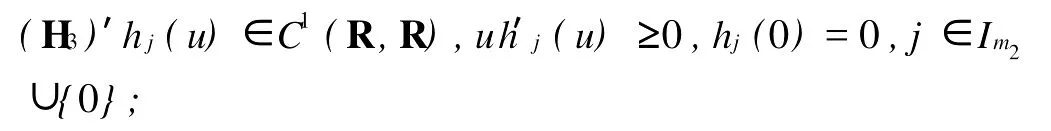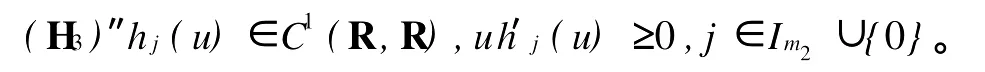具非线性扩散系数的中立抛物型方程的振动结果*

罗李平,杨 柳

(衡阳师范学院数学与计算科学系,湖南衡阳421002)

偏泛函微分方程来源于动力学、生物遗传工程、控制论和人口动力学中众多的数学模型,具有强烈的实际背景。文献[1]在研究一维时滞扩散方程边值问题时最早提出了一类时滞抛物型方程解的振动性问题,文献[2]首次研究了一类中立双曲型方程解的振动性问题。之后,关于时滞(中立)双曲型或抛物型方程解的振动性研究,已取得许多很好的成果,参见文献[3-8]。相对而言,关于非线性扩散系数情况下的双曲型或抛物型方程解的振动性的研究还不多见。本文在上述文献的基础上,利用新的处理非线性方程非线性项的方法,讨论一类特殊的具非线性扩散系数的中立型抛物方程在Robin边值条件下解的振动性问题,通过将这类方程解的振动判别问题转化为时滞微分不等式最终正解的存在性问题,建立了判别其所有解振动的不需要利用特征值的若干充分条件,所得结果充分表明了时滞量的决定性作用。

考虑如下的中立抛物型方程

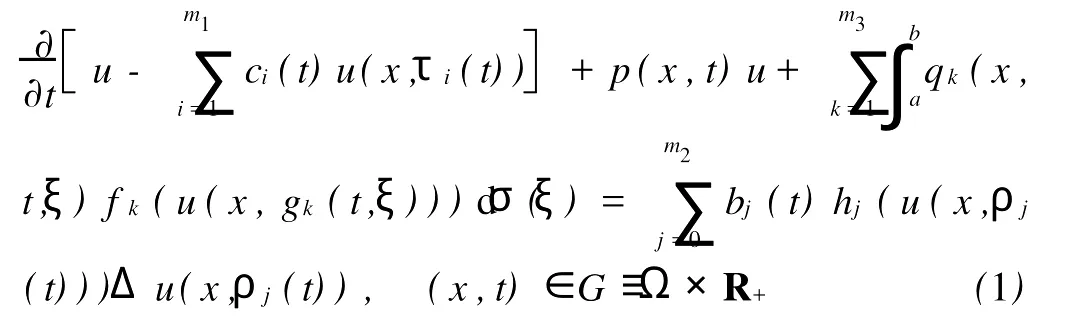
其中Ω

同时考虑如下的Robin边值条件:

其中N表示9Ω的单位外法向量,β(x)∈C(9Ω)。

本文总假设下列条件成立:

定义1 问题(1),(2)的解u(x,t)∈C2(G)∩C1(?G)在G内称为振动的,若Πμ>0,存在点(x0,t0)∈Ωx[μ,∞),使得u(x0,t0)=0成立;否则称为非振动的。

定理1 若微分不等式

无最终正解,则问题(1),(2)的所有解在G内振动。

证明 假设问题(1),(2)有1个非振动解u(x,t),不失一般性,设u(x,t)>0,(x,t)∈Ω×[μ,∞),μ≥0(u(x,t)<0的情形,令,类似可证明之),则由条件(H1),(H2)知,存在t1≥μ,使得gk(t,ξ)≥μ,(t,ξ)∈[t1,∞)×[a,b],且有τi(t)≥μ,ρj(t)≥μ,t≥t1,因此u(x,gk(t,ξ))>0,(x,t,ξ)∈Ω×[t1,∞)×[a,b],u(x,τi(t))>0,u(x,ρj(t))>0,(x,t)∈Ω×[t1,∞),i∈Im1,j∈Im2,k∈Im3。

在区域Ω上方程(1)两边关于x积分,得

由Green公式,边值条件(2)及(H3)有

其中d S是9Ω上的面积元素。

由(H4)有

交换积分顺序并由Jensen不等式及(H4)有

U(t)是微分不等式(3)的一个最终正解,而这与定理1的题设矛盾。证毕。

引理1[9]设非减,且若

存在i∈Im,使得

则微分不等式

无最终正解。

定理2 设下列条件成立:

若存在k∈Im3,使得

则问题(1),(2)的每一个非零解在G内振动。

证明 假设问题(1),(2)有1个非振动解u(x,t),不失一般性,设u(x,t)>0,(x,t)∈Ω×[μ,∞),μ≥0,则类似于定理1的证明知,存在t1≥μ,使得u(x,gk(t,ξ))>0,(x,t,ξ)∈Ω×[t1,∞)×[a,b],u(x,τi(t))>0,u(x,ρj(t))>0,(x,t)∈Ω×[t1,∞),i∈Im1,j∈Im2,k∈Im3,且有微分不等式(8)。于是结合(H7),由式(8)可得

由式(11)易知,Z′(t)≤0,t≥T1,即Z(t)在[t1,∞)上非增。注意到条件(H6),知Z(t)不会最终为零。下证Z(t)>0,t≥t1。事实上,若Z(t)<0,则可推得U(t)有界,t≥t1。倘若不然,则存在序列{tn}<[t1,∞),使得且于是结合(H6)有

由U(t)有界知,存在2个序列{tn},{t*n}<[t1,∞),使得且

在(13),(14)式中,分别令n→∞,并结合(H6),可得

于是由(15),(16)式可得

因此Z(t)>0,t≥t1。显然Z(t)是微分不等式(11)的1个最终正解。但据(9)及引理1知,(11)无最终正解,矛盾。证毕。

注:利用本文的方法可以类似地讨论方程(1)分别满足Dirichlet边值条件

或Neumann边值条件

的解的振动结果。只要将文中的假设条件(H3)分别改为:

或

[1] Kreith K,Ladas G G.Allowable delays for positive diffusion processes[J].Hiroshima Math J,1985,15:437-443.

[2] Mishev D P,Bainov D D.Oscillation p roperties of the solutions of a class of hyperbolic equations of neutral type[C].//Differential Equations:Qualitative Theory.Hungary:Colloquia Mathematica Societaits Jonos Bolyai,47 Szeged,1984.

[3] Yu Y H,Liu B,Liu Z R.Oscillation of solutions of nonlinear partial differential equations of neutral type[J].Acta Math Sini,1997,13(4):563-570.

[4] Wang P G,Wu Y H.Forced oscillation of a class of neutral hyperbolic differential equations[J].J ComputAppl Math,2005,177(2):301-308.

[5] 罗李平.非线性双曲型泛函偏微分方程系统解的振动性[J].中国海洋大学学报:自然科学版,2008,38(3):495-496.

[6] LiW N,Cui B T.Necessary and sufficient conditions for oscillation of neutral delay parabolic differential equations[J].Appl Math Comput,2001,121(1):147-153.

[7] Wang PG,Teo KL.Oscillation of solutions of parabolic differential equations of neutral type[J].JMath Anal Appl,2005,311(2):616-625.

[8] 罗李平.非线性中立抛物型偏微分方程系统的振动性定理[J].数学的实践与认识,2009,39(6):198-202.

[9] Ladde GS,Lakshmikantham V,Zhang B G.Oscillation theory of differential equationswith deviating arguments[M].New York and Basel:Marcel Dekker Inc,1987.