改进BP算法在风暴潮极值水位预报中的应用*
2011-01-10侯一筠
纪 芳,侯一筠
(1.中国科学院海洋研究所,山东青岛266071;2.中国科学院研究生院,北京100049)
人工神经网络(Artificial Neural Networks,ANN),是1种模仿动物行为特征,进行分布式并行信息处理的算法数学模型[1]。这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的。
互相连接的方式称为连接模式。神经元之间的连接强度称为突触权或连接权。当网络的连接权矩阵确定后,网络的连接模式也就随之确定。因此,连接模式也称作网络的连接权矩阵,它是对生物神经网络中的突触连接强度的模仿。人工神经网络具有自学习和自适应的能力,可以通过预先提供的一批相互对应的输入-输出数据,分析掌握两者之间潜在的规律,最终根据这些规律,用新的输入数据来推算输出结果,这种学习分析的过程被称为“训练”。
风暴潮指由强烈大气扰动,如热带气旋(台风)、温带气旋(寒流)等引起的海面异常升高现象。沿海验潮站或河口水位站所记录的海面升降,通常为天文潮、风暴潮、地震及其他长波振动引起海面变化的综合特征。一般验潮装置已经滤掉了数秒级的短周期海浪引起的海面波动。如果风暴潮恰好与天文高潮相叠(尤其是与天文大潮期间的高潮相叠),加之风暴潮往往夹狂风恶浪而至,溯江河洪水而上,则常常使其影响所及的滨海区域潮水暴涨,甚者海潮冲毁海堤海塘,吞噬码头、城镇和村庄,从而酿成巨大灾难[2]。因此对于风暴潮的预报,极为引人关注。海浪预报的难点在于产生浪的风本身具有很大的随机性和复杂性,造成浪的预报十分困难。关于海浪生成的物理机制,至今尚未得到十分圆满的解决。因此,积极探索风浪预报的新方法、新思路就显得很有必要。
人工神经网络以其高度的非线性表达能力,比较适合于台风风暴潮极值预报这一多因子、多目标的拟合、预测,其特有的拓扑结构和处理信息的方法,能够有效地解决一些传统方法难以解决的问题。它明显的优点是具有较好的自适应学习和非线性映射能力,容错能力强,预报速度快,比较适合处理那些物理机制复杂,因果关系和推理规则难以确定的非线性问题[3]。因此它的这些特点都为运用到台风浪预报中提供了可能。
1 标准BP算法
多层前馈神经网络的反传学习理论(即BP)最早由Werbos在1974年提出,并由Rumelhart等在1985年发展为BP算法[4]。BP算法实际上是工程上最常用的最小均方误差算法的1种广义形式,它使用梯度最速下降搜索技术,按网络的实际输出和期望输出的均方误差最小的准则递归求解网络的权值和各节点的阈值。
BP算法属于有导师的学习算法[5]。其主要思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输入层传人,经各隐含层逐层处理后,传向输出层。若输出层的实际输出与期望的输出不符,则转入误差的反向传播阶段。将输出误差以某种形式通过隐含层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。信号正向传播与误差反向传播的各层权值调整过程周而复始地进行。此过程一直进行到网络输出的误差减少到可接受的程度,或进行到预先设定的学习次数为止。对于m个学习样本:X1…Xm,已知其对应的输出样本为:Y1…Ym。学习的目的是用网络的实际输出O1…O m与目标矢量Y1…Ym之间的误差来修改其权值,使O与期望的Y尽量接近,即网络的输出层的误差平方和达到最小。
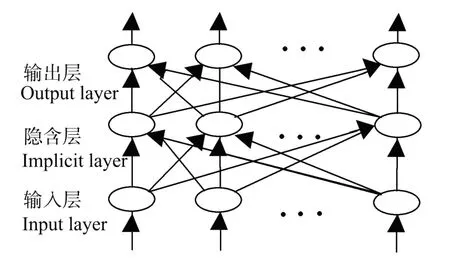
图1 BP网络结构示意图Fig.1 BP neural network structure
2 改进BP算法
BP算法由于其具有实现任何复杂非线性映射的功能、具有自学习能力以及一定的推广概括能力,在很多方面得到了广泛的应用。但是它也存在自身的限制和不足,其主要表现在它的训练过程的不确定上。主要缺点为:学习效率低、收敛速度慢;容易陷入局部极小点;完全不能训练。Cauchy训练[4]虽然训练速度较慢,但它的最大长处是,在训练中,连接权的调整时随机的,它有可能使网络逃离局部极小点。因此,本文将结合Cauchy训练和BP算法得到1种改进的BP算法。该算法具有BP算法的联接权调整量确定的优点,又具有Cauchy算法中联接权调整随机性和试探性所带来的可以逃离局部极小点的优点。
BP算法与Cauchy算法相结合[4],由BP算法提供直接计算部分计算联接权的调整量,wij=wij+Δwij;Cauchy算法提供随机部分,按照Cauchy训练来计算联接权的调整量。Δwij=α((1-β)δjoi+βΔwij′)+(1-α)Δ。α∈(0,1)为学习率,β∈(0,1)为冲量系数。
改进算法的具体描述如下:
[1]初始化各层的联接权矩阵W;定义人工温度T的初值;初始化λ、控制精度ε
[2]E=0;
[3]从样本集中取出一样本(xP,yP);按均匀分布在[0,1]区间取一随机数r;
若r<λ则执行以下程序:
(a)计算出理想输出与实际输出的差EP;E=E+EP;计算输出层调整权Δw;调整W(M);对每层神经元按照指数平滑的方法计算;调整隐含层的W(h)。
若r>λ则执行以下程序:
(b)计算其输出与目标函数E=({W});依次选取{W}中每一个W(h),按照Cauchy分布计算出W(h)的1个调整量ΔW(h);根据{W(h)+ΔW(h)}重计算相应目标函数和输出ΔE=E({W(h)+ΔW(h)})-E({W});E({W(h)+ΔW(h)});如果ΔE<0则调整W(h)为W(h)+ΔW(h);否则按照以下概率P(E({W(h)+ΔW(h)}))=exp(-来调整W(h)为W(h)+ΔW(h);
[4]如果E小于控制精度ε或T足够小则结束,否则继续[2]。
3 模型建立
通常,BP神经网络的输入变量即为待分析系统的影响因子或自变量数,一般根据使用者需要求解问题来确定。输出变量即为系统待分析的系统性能指标或因变量,可以是1个或多个。影响台风风暴潮的因素有很多。针对确定的预报地点,它与该地点的风区、风时、风速、风向、底摩擦及研究海区海水深浅等有关。但是,对于某一确定地点,除风场外,其他因素对风浪的影响可近似地认为是相同的。风速对风暴潮有明显的影响;在开阔海域,风向对风暴潮浪高的影响具有各向同性的效果,但是在近岸海域,风向的作用则有所不同。风向不仅对风暴潮的波向有重要影响,对风暴潮的浪高也同样作用显著。另外,台风的移向、移速也是影响台风风暴潮的重要因素。因此要做好台风风暴潮的预报就要研究这些因素对台风浪的影响。
倘若选取的因子过多,会使得建立的网络不够稳定,网络模型对样本拟合会存在拟合值上周期性小波的存在以及由此带来的拟合误差[6-7]。一般来说,台风风速与台风风暴潮极值浪高有较好的相关关系,通常风速越大,所对应的台风风暴潮浪就越高;台风风暴潮浪高与台风中心气压的对应关系不是那么的明显。台风风暴潮浪高与台风中心距预报海区的距离关系显著,台风中心距预报海区的距离越近,所对应的浪高越高。因此,本文只选取对风暴潮极值水位影响比较显著的4个因子,即台风中心距预报海区距离、预报海区的台风强度、风速和台风移速,作为输入因子,而把台风风暴潮的极值水位作为预报输出因子,分别运用BP算法和改进的BP算法来构建非线性风暴潮极值水位网络预报模型。
4 实验及结果分析
本文选取山东某站点的每年台风风暴潮资料,分别运用BP算法和改进BP算法,建立台风强度、风速、和台风移速与风暴潮极值水位的非线性网络预报模型。根据站点的每年台风风暴潮资料,对该站的风暴潮极值水位进行预报。通过对实验结果进行对比比较,以此来验证改进BP算法的可行性与准确性。
在所取26个个例中,选取其中的20个个例,分别运用2种算法对训练样本进行网络模型的训练。为了加快计算和收敛的速度,对输入因子作了归一化处理。对训练样本训练、拟合1 000步以后,实验结果见图2(图中*号为实际的极值水位值,实线为拟合曲线):
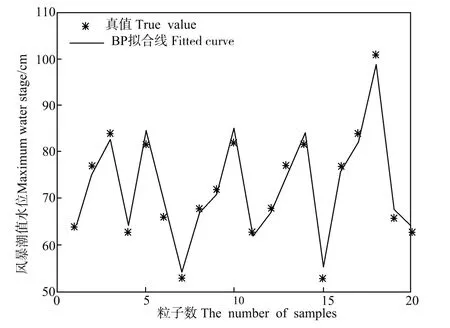
图2(a) BP网络训练样本的极值水位拟合效果Fig.2(a) BP neural network sample fitted curve of maximum water stage
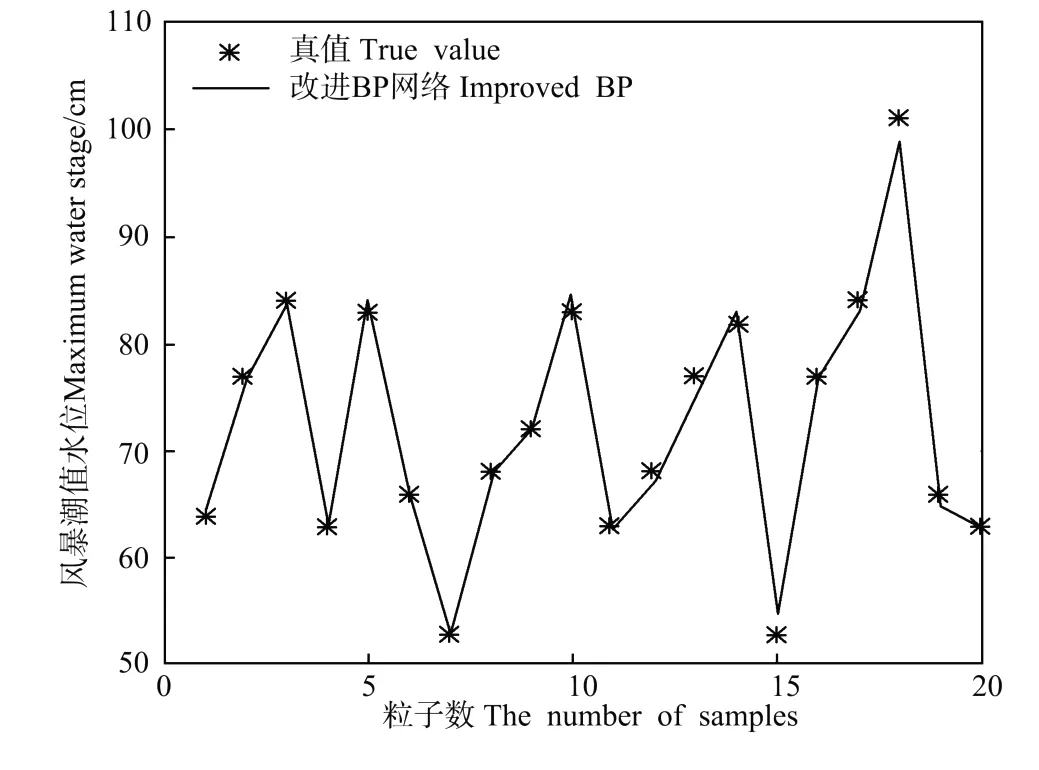
图2(b) 改进BP网络训练样本的极值水位拟合效果Fig.2(b) Imp roved BP neural netwo rk sample fitted curve of maximum water stage
从图中可以看出,BP网络模型与改进的BP网络模型都有很好的历史样本拟合能力。但是通过对比图2(a)与图2(b)可以看出,改进的BP算法的实验效果要好于原来的BP算法,拟合程度要更高一些。在实际的运用中,网络好坏的关键是看能否说明网络模型的预报结果。因此,取剩下的6个极值水位个例进行检验,分别以BP网络以及改进的BP网络运用上述的技术原理与方法,网络模型的预报极值水位实验结果见图3。
从图3(a)与图3(b)可以看出,建立的网络模型对预报极值水位的结果与实际值基本接近,只是个例2的预报结果与实际值相差较大一点,但是从整体上看,预报结果是较为理想的,这就说明所建网络模型对实际风暴潮极值水位的描述和预报是可行、可用的。
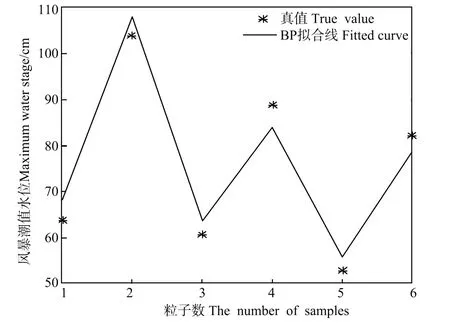
图3(a) BP网络模型的预报极值水位检验Fig.3(a) BP neural network sample test curve of maximum water stage
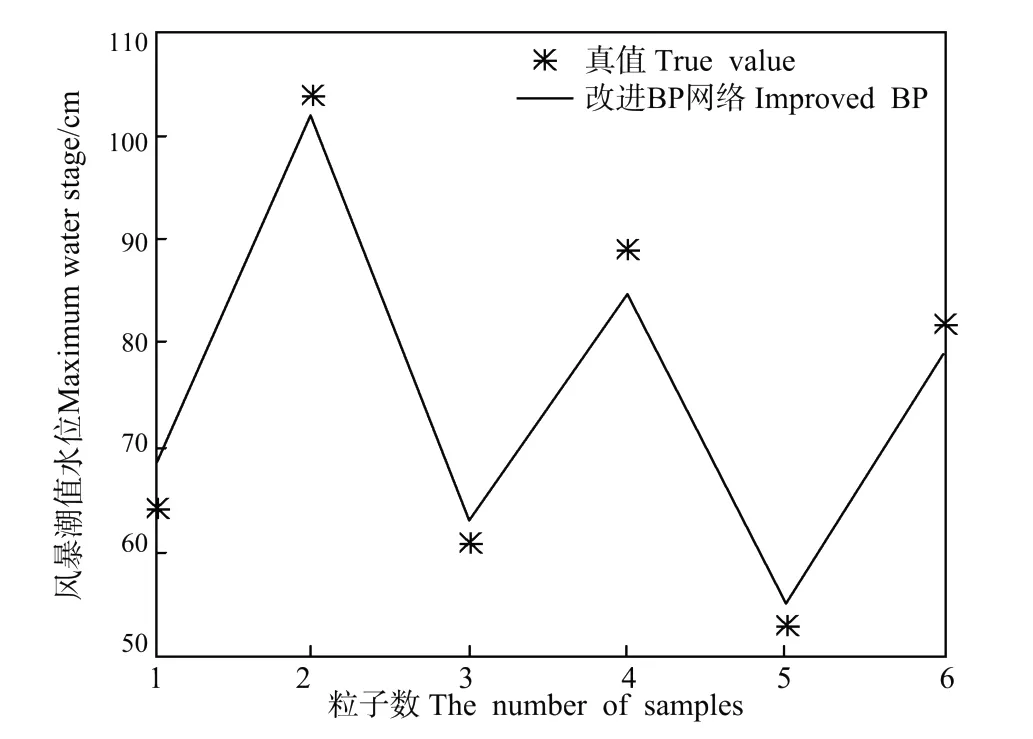
图3(b) 改进BP网络模型的预报极值水位检验Fig.3(a) Imp roved BP neural network sample test curve of maximum water stage
通过表1中BP网络模型与改进的BP网络模型预报极值水位误差对比,可以看出在训练拟合和检验2方面,改进的BP算法均比原先的BP算法效果要好。证明了改进算法的正确性与可行性。
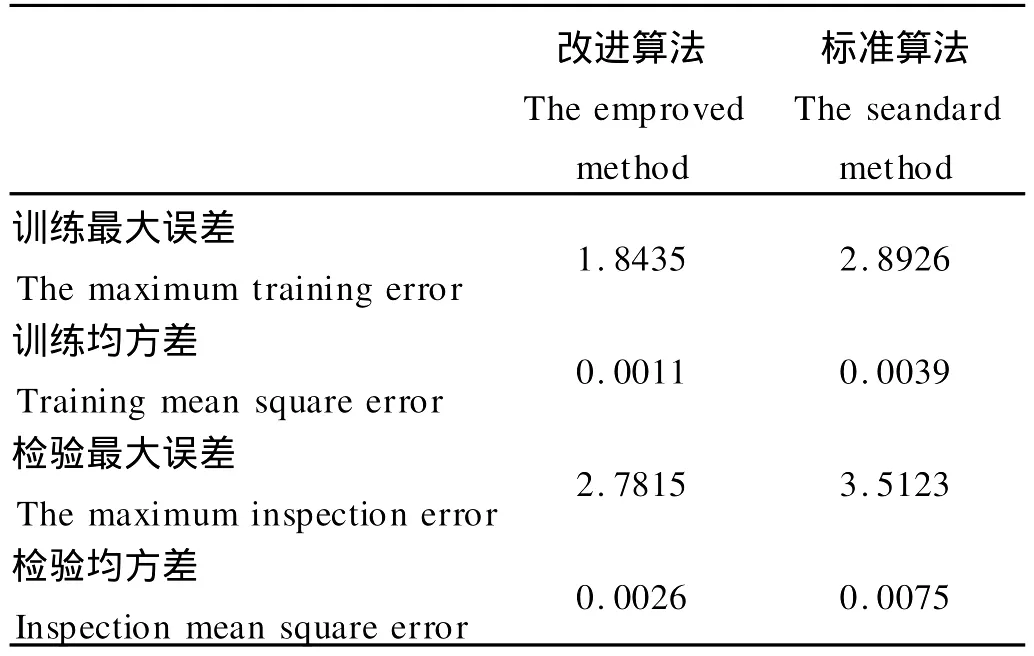
表1 BP与改进BP网络模型误差对比图Table 1 The error comparison of BP neural network and imp roved BP neural network
5 结语
本文通过采用Cauchy训练与传统BP算法相结合的方法,对传统BP算法进行了改进,并将改进算法用于台风风暴潮极值水位预报中。经M atlab仿真实验结果表明,改进的算法取得了令人满意的效果,网络所表现出的稳定性以及准确性都比传统算法性能优越。新的算法为神经网络算法的研究和训练拓宽了思路,提供了新的研究途径,同时也为台风风暴潮极值水位预测提供了新思路。
[1] 张韧.用MA TLAB中的Neural Network toolbox仿真赤道太平洋SST的预报模型[J].海洋科学,2001,25(2):38-41.
[2] 沙文钰.风暴潮、浪数值预报[M].北京:海洋出版社,2004.
[3] 张立明.人工神经网络的模型及其应用[M].上海:复旦大学出版社,1994:11.
[4] 蒋宗礼.人工神经网络导论[M].北京:高等教育出版社,2001:55-56.
[5] Galvan M,Isasi P,A ler R,et al.A selective learning method to imp rove the generalization of multilayer feedforward neural networks[J].International Journal of Neural Systems,2001(2):167-177.
[6] 王科俊,王克成.神经网络建模、预报与控制[M].哈尔滨:哈尔滨工程大学出版社,1996:37.
[7] 薛彦广,沙文钰,徐海斌,等.人工神经网络在风暴潮增水预报中的应用[J].海洋预报,2005,22(2):35.
