利用连续小波提取近海大气湍流中的相干结构*
2011-01-10盛立芳
姚 菡,盛立芳,2,贺 赟,黄 健
(1.中国海洋大学海洋气象学系,山东青岛266100;2.中国海洋大学物理海洋实验室,海洋-大气相互作用与气候实验室,山东青岛266100;3.中国气象局广州热带海洋气象研究所,广东广州510080)
相干结构,又称拟序运动或拟序结构,是近代湍流研究中的重大发现。它在切变流场中不规则地产生,运动产生的起始时刻和位置是不确定的,但是一经触发,便以某种确定的次序发展为特定的运动状态[1],是湍流中在时间和空间上具有自组织特性的大尺度脉动结构[2]。
大气湍流造成流场中各部分之间强烈混合,在大气边界层物质质量、能量和动量的交换过程中起着重要的作用,而相干结构又决定着湍流脉动的生成、演化和发展,因而通过流动的测量提取大气湍流中的相干结构并研究其运动学和动力学特性,具有重要的理论价值和实际意义。早期相干结构的试验研究中所采用的条件采样方法,如mu-level法、象限分解法和V ITA法等,在经验参数选取上具有主观性,并且无法得到相干结构的发展过程[3]。而小波变换的方法可以排除经验阈值选择中所产生的主观因素的影响,有效地给出湍流相干结构主导尺度。同时,小波函数具有快速衰减和有限支撑的特点,在空间和频域上具有良好的局部性,通过伸缩、平移变换,可以合理保留并模拟湍流脉动的局部结构信息和涡旋特征[4],从而为相干结构的辨识提供更为客观合理的方法。
早在1992年Farge[5]就系统总结了小波变换在湍流中的应用,并创造性提出用连续小波变换研究相干结构的动力特征,进而为湍流大涡模拟技术提供新的方法。随后Gamage和Hagelberg[6]用局域小波分析研究了微锋及相伴随的相干结构,Gao和Li[7]用小波方法研究了大气和森林交界面上的相干结构,Coulter和Li[8]用小波变换系数方差极大值辨识行星边界层中的相干结构。但是,这些研究只给出了相干结构尺度的判别方法,并没有提取相应的相干波形。汪健生等[9]和刘海峰等[10]分别提出了基于连续小波变换的相干结构重构公式,WJ.Staszew ski和Worden[11]提出了基于正交小波基的重构公式。需要指出的是,对于离散小波变换,尺度因子往往以2的幂次方形式选取,无法准确给出相干结构的尺度。而连续小波在尺度上可以给出几乎连续的描述,克服离散正交小波在大尺度处存在低分辨率的问题,从而可以更加准确的定位相干结构的尺度。
以往南海大气湍流的研究工作主要集中在通量以及湍流统计量特征上,并没有涉及对南海海域大气湍流相干结构的研究。马耀明等[12]给出了南沙海域湍流热通量输送、方差相似性、风速各分量谱、温度谱及各湍流通量协谱等大气湍流结构和输送特征,并与陆地下垫面上的结果进行了比较。闰俊岳等[13]基于南海季风实验(SCSM EX)的观测结果给出了南海季风爆发期间近海面层大气湍流强度,相似函数,摩擦速度,空气动力粗糙度长度,曳力系数等湍流统计量分布特征。本文结合小波分析的方法考察了南海海域大气湍流相干结构特征。通过对南海塔基湍流风脉动资料进行连续小波分析,由能量极大值判别法则[9-10,14]确定大气湍流在3个风速分量方向上的相干结构尺度,并根据相应的小波重构公式,提取各个尺度上的相干波形。进而对小波系数进行谱分析,结合相干结构的生成周期和时间尺度,考察南海大气湍流相干结构的生成及演变特征。最后,根据观测期间天气形势以及相应时段湍流统计特征,进一步探讨了典型天气条件下相干结构的能量分布以及随时间的变化特征。
1 观测资料及预处理
1.1 资料介绍
湍流资料来自南海近海的观测铁塔,观测点位于广东省茂名市电白县电城镇莲头半岛以南的海上观测平台,其南侧为广阔的南海水域。该平台是我国目前已建成的第1个海洋气象专业观测平台,距离陆地远(离岸6.5km),获得的数据有良好的海洋代表性,并且观测受塔体自身影响小,可进行全方位观测。观测实验中采用美国Campbell公司生产的CSA T3超声风速仪测量三维风速,采样频率为10 Hz。
1.2 数据处理方法及步骤
去除奇异点 根据莱以特准则,当观测值与30 min平均值之差大于4倍标准差时判定为奇异点,并用前1个数据代替以保持数据的连续性。当奇异点的个数超过数据总长度的1%,则认为观测数据无效。
坐标旋转 为了消除因观测仪器安装倾斜或下垫面不平坦等因素对观测结果造成的影响,通常需要先通过坐标轴旋转对超声风速仪测得的风速进行校正[15],使u分量代表主导风方向,v分量代表风的侧向分量,w分量代表风的垂直分量,并令垂直平均风速为0,以满足通量观测的假设条件。本文采用二次坐标旋转的方法进行风速校正[16]。
时间平均及趋势去除 本文采用湍流研究中常用的30 min作为平均时间长度[17]。在对选取的30 m in湍流资料进行相干结构辨识和提取时利用高通滤波去除了大于1 000 s尺度的趋势和大结构,而在考察一定天气形势下相干涡旋能量结构时,为了获得更广范围内相干结构尺度分布特征,并没有进行滤波处理。
2 分析方法
2.1 小波变换
小波分析是在傅里叶分析基础上发展起来的,自适应的时频分析方法,具有很强的表征信号局部特征的能力。对于给定的小波函数Ψ(t),其傅里叶变换满足以下允许性条件,则时间序列f(t)∈L2(R)的连续小波变换为
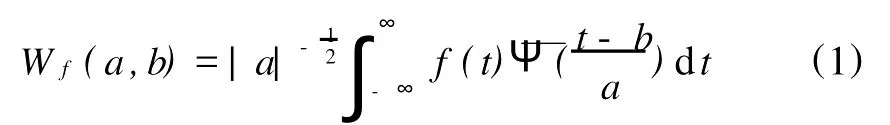
其中,Wf(a,b)为小波变换系数的共轭函数则是由母小波Ψ(t)通过尺度因子a和平移因子b作用得到的小波序列。在研究大气边界层的相干结构时采用a-1作为小波系数的归一化因子,可以有效地保持变换前后不同尺度上能量相对大小,同时识别某个时间尺度上更大范围的峰值[2]。此时,小波变换系数定义为

令C′Ψ=CΨ/2,对于给定尺度a处小波能量为
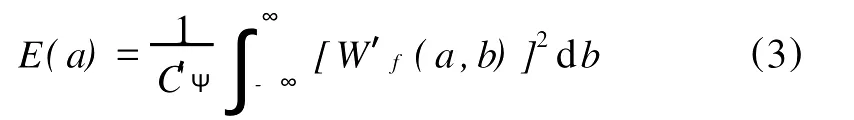
根据相干结构辨识的能量极大值准则,认为能量极大值对应的尺度a*为相干结构的主导尺度。根据小波逆变换公式,可以得到相干结构波形的反演公式

本文在通过小波变换方法提取并分析大气湍流中的相干结构时采用Mo rlet小波作为母小波。Mo rlet小波可以有复值函数和实值函数2种形式。复值Mo rlet小波函数的表达式[18]为Ψ(t)=eiΩte-t2/2,其中Ω≥5为常数,在本文运算中取为2π。
2.2 谱分析
基于Fourier变换的功率谱分析在早期湍流研究中发挥着极其重要的作用。Kolmogo rov关于局地均匀各向同性湍流能谱的惯性区标度不变理论是20世纪湍流研究最重要的理论成果之一。
本文利用Fourier变换对不同尺度上湍流小波系数进行能谱分析,考察不同尺度上相干结构的生成周期,从而结合相干结构的生命尺度和生成周期描述其变化特征。
3 大气湍流相干结构分析
3.1 辨识并提取相干结构
本文首先对三维风速进行个例分析,利用小波分析的方法辨识并提取其相干结构。选取的分析资料为2009年9月3日18··00~18··30时长30 min的风脉动资料,该时段内天气状况平稳,东南风受陆地影响很小。
对经过预处理的三维风速资料进行连续小波变换,根据(3)式,对表征时间的平移因子b求积分可以得到所选时段内不同尺度a处对应的小波能谱密度。由于分析样本的长度有限,本文的分析不可能包含所有尺度的相干结构,而且较大的相干结构可能并不完全由湍流产生[2]。本文在对大气湍流相干结构进行辨识和提取时,根据目前对大气边界层相干结构的研究[7-8,19-20],仅取1~100 s尺度进行分析。图1为风速U分量的小波能谱曲线,其中横坐标用和傅里叶变换相对应的时间(空间)尺度特征量频率f来表征相干结构的尺度大小,它和小波变换中尺度a是一一对应的。可以看到在f≈0.017 Hz,即尺度a=46 s处,存在能量的极大值。根据相干结构的能量极大值辨识法则,可认为此处为U方向风速相干结构所对应的频率或尺度。然后,利用小波逆变换提出的相干结构重构公式,可以获得此相干结构对应的波形。
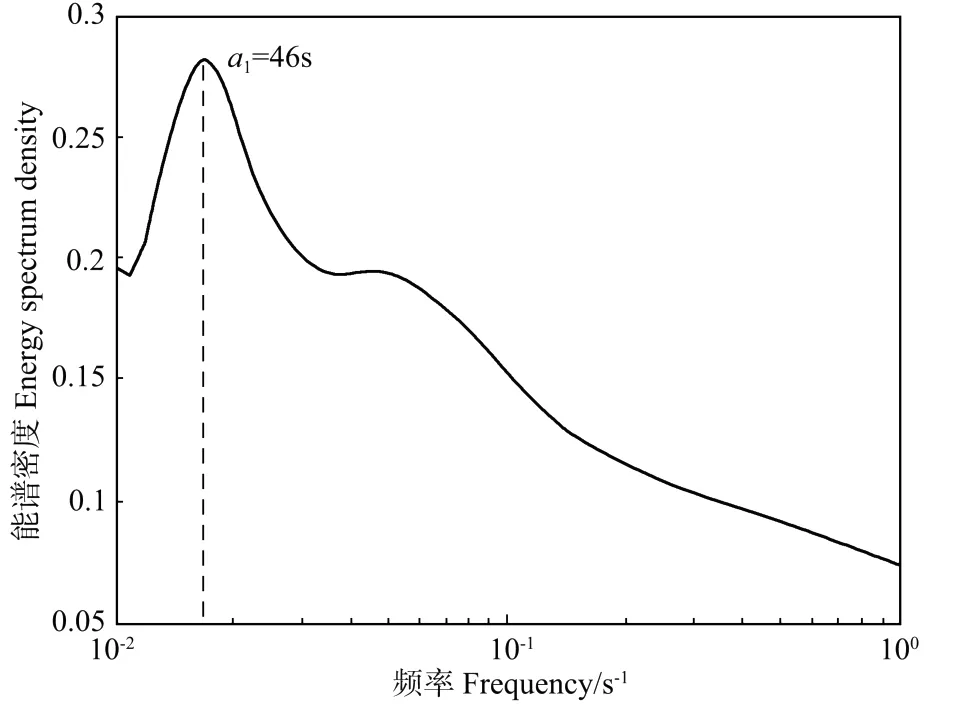
图1 风速分量U的能谱曲线Fig.1 Wavelet energy spectrum of Ucomponent of wind speed
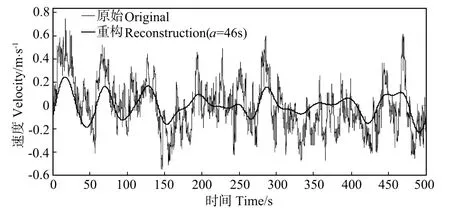
图2 U分量原始信号与相干波形比较Fig.2 The comparison between the original signal and the coherent structure of U component
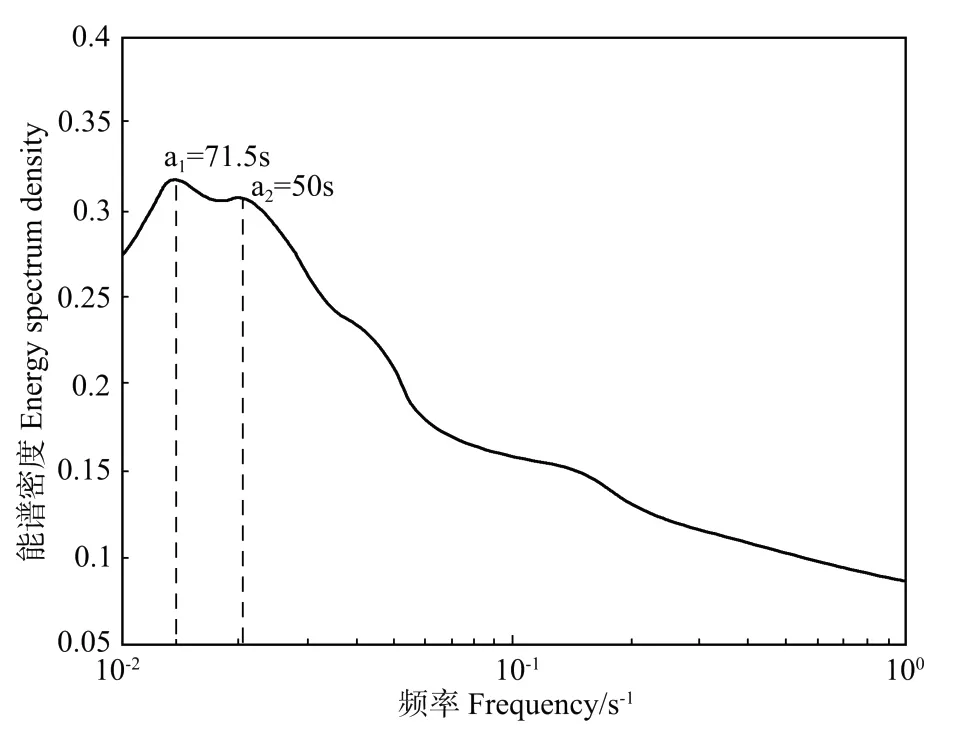
图3 风速分量V的能谱曲线Fig.3 Wavelet energy spectrum of Vcomponent of wind speed
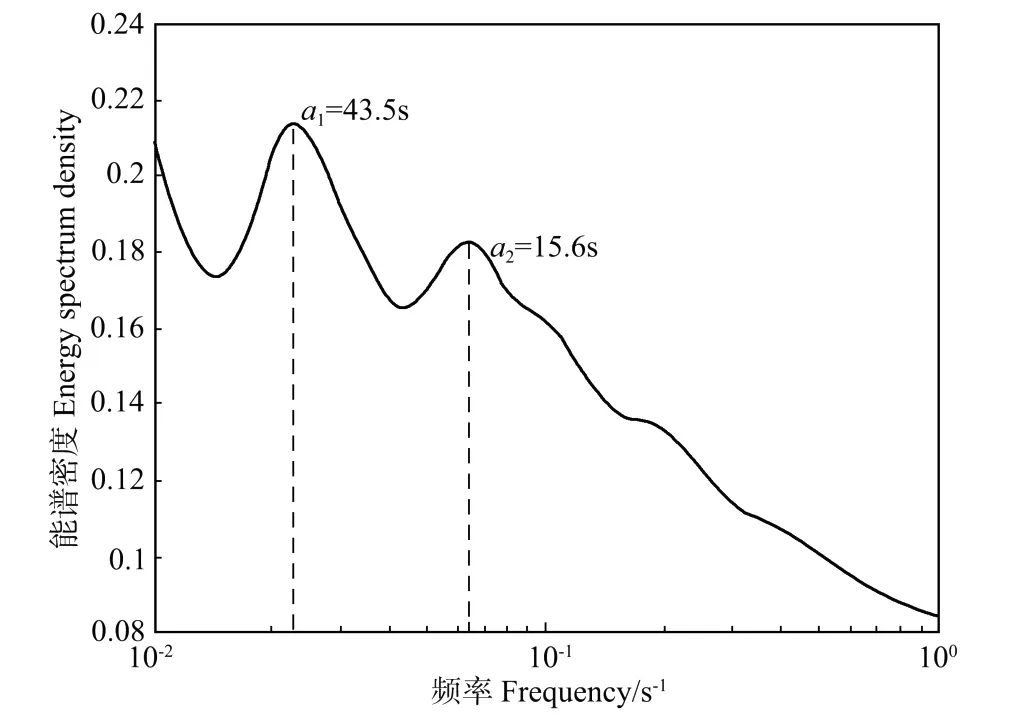
图5 风速分量W的能谱曲线Fig.5 Wavelet energy spectrum of Wcomponent of wind speed
图2给出风速U分量的相干结构重构波形和原始信号的比较,为方便分析,图中时长仅取其中500 s。对于风速V分量,也可以通过小波变换给出其能谱曲线,并根据其能量的极值确定相干结构所对应的频率或尺度。如图3所示,对于V分量,能谱曲线在分析频段表现为2个主要的峰值,分别对应尺度a1≈71.5 s以及a2≈50 s,说明风速分量可以存在多尺度的相干结构。图4给出它们各自以及共同的重构波形。图5给为风速W分量的小波能谱曲线,其在分析频段内同样存在2个峰值,其中主峰值位于a2≈43.5 s处,而次峰值位于a≈15.6 s。同样的,根据重构公式,提取相应的相干结构,图6为其不同尺度上各自及共同的重构波形与原信号的对比。
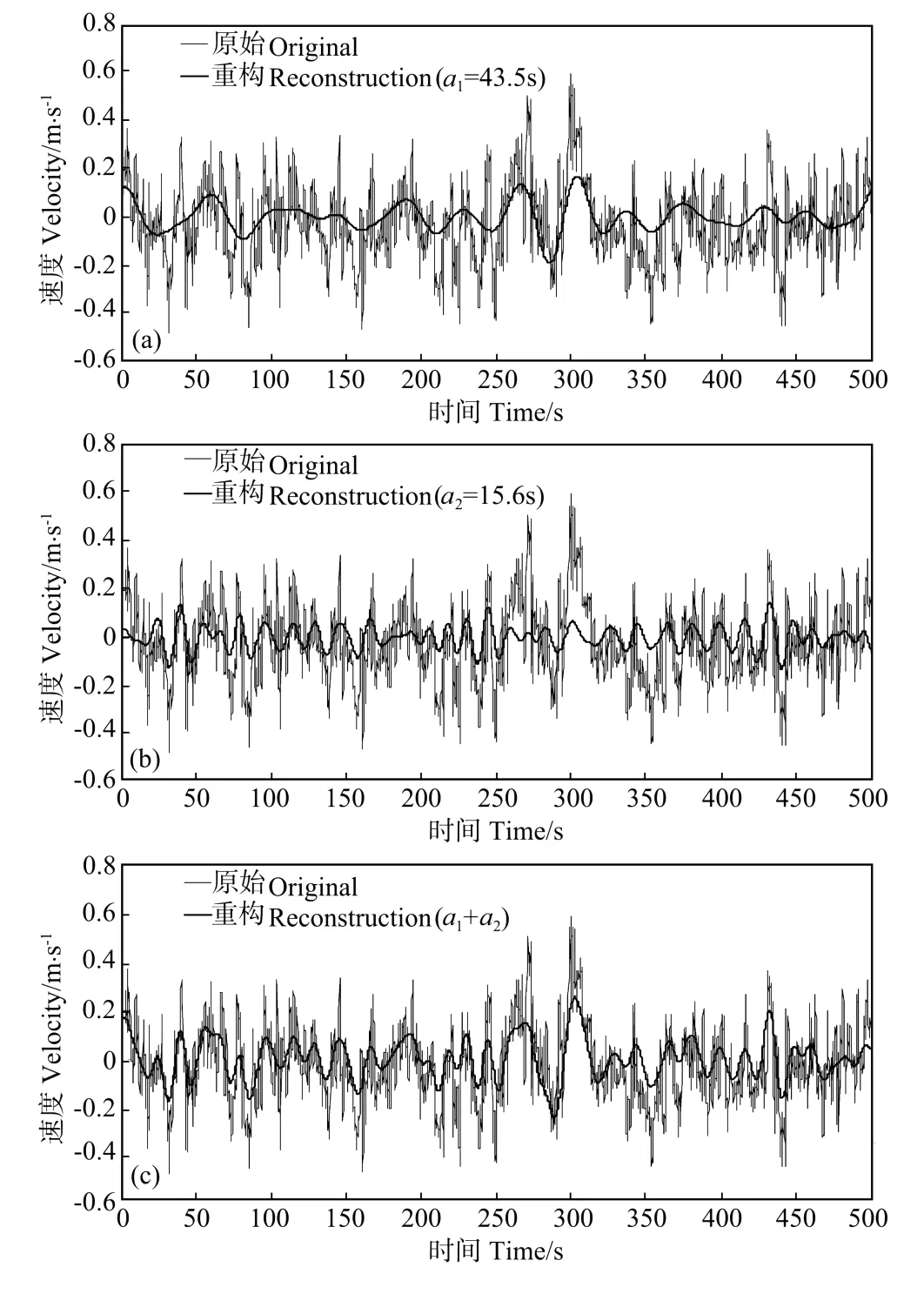
图6 W分量原始信号与相干波形比较Fig.6 The comparison between the original signal and the coherent structure of Wcomponent
通过比较3个方向湍流速度的小波能谱,相干结构在能量上具有相同的量级,本例中,E(va)>E(ua)>E(wa),但不同样本的实验表明此规律不具有普适性。本文中提取的风速分量相干结构的尺度与Gao和Li[7]在大气和森林交界面,陈炯等[19]在城市冠层以及Li Xin等[20]在稻田上空得到的相干结构具有大致相同的量级,并且比实验室湍流相干结构的尺度[21]大3个量级。多组数据重复试验的结果表明,大气湍流各个风速分量都可能存在多个尺度的相干结构,如本例中的V分量和W分量。湍流相干结构具有多尺度的特性,它们在不同尺度流动中发挥的作用是不同的,不同尺度相干结构的综合作用制约影响着湍流整体的流动特征。
从重构的相干波形可以看出,小波逆变换提取了对应频率(尺度)的准周期结构,其在波形和数值上与湍流信号吻合的较好,体现了湍流中间尺度的结构。所提取的相干波形的量值大小反映了相干结构的强输运特征,而剩余的非相干信号则主要体现湍流中小尺度、不规则、强间歇性的部分。对于存在多尺度相干结构的情况,如本例中的V分量和W分量,不同尺度上的相干结构均能反映其对应的准周期性变化,它们的共同作用可以很好的反映湍流信号在分析频段内的波形结构。
3.2 小波系数谱分析
对各个尺度上小波系数分别进行傅里叶变换,可以得到不同尺度对应的波动在频域上的能量分布,从而考察相干结构的尺度和生成周期之间的关系[22-23],进一步描述时间序列中相干结构的变化规律[2]。在小波系数谱分析图(见图7)中,横坐标为傅里叶变换的频率,用以刻画相干结构的出现频次,即生成周期;纵坐标对应于小波分析的尺度,用频率表征相干结构的生命尺度,即持续时间。不同尺度上小波系数的能谱量值在图中用等值线标示,其中虚线处相干结构的生成周期和持续时间大致相同。
根据小波系数谱分析的结果,在分析频段内,相干结构发生的时间间隔和其生命尺度相近,说明相干结构是连续生成的。同时,风速V分量和W分量的小波系数谱分析显示,较小尺度上涡旋结构以不连续出现为主。如图7b所示,对于经向风速V,0.1~0.2 Hz的涡动能量出现的主要频次约为0.011 s-1;垂向风速W也存在生成周期大于其生命尺度的小尺度涡旋结构(见图7c)。
将小波系数谱分析图与小波能谱曲线进行比较,结果显示,两者所反映出的相干结构主要尺度基本吻合。并且,小波谱比傅里叶谱具有更高的分辨率,小波能谱曲线具有更明显的孤立峰值,所以能够更加清楚地给出相干结构尺度所在的位置。
湍流涉及的是自由度非常大的敞开的非稳态的耗散体系[3],不存在湍流的主导尺度。利用小波系数能量极大值准则识别相干结构是对不同尺度湍涡能量在时间上的平均,不同尺度湍涡结构的生命尺度不同,它们并不一定贯穿于观测的始终,但是根据小波系数谱分析的结果,在一定频段范围内,大气湍流相干结构主要以连续的方式产生。
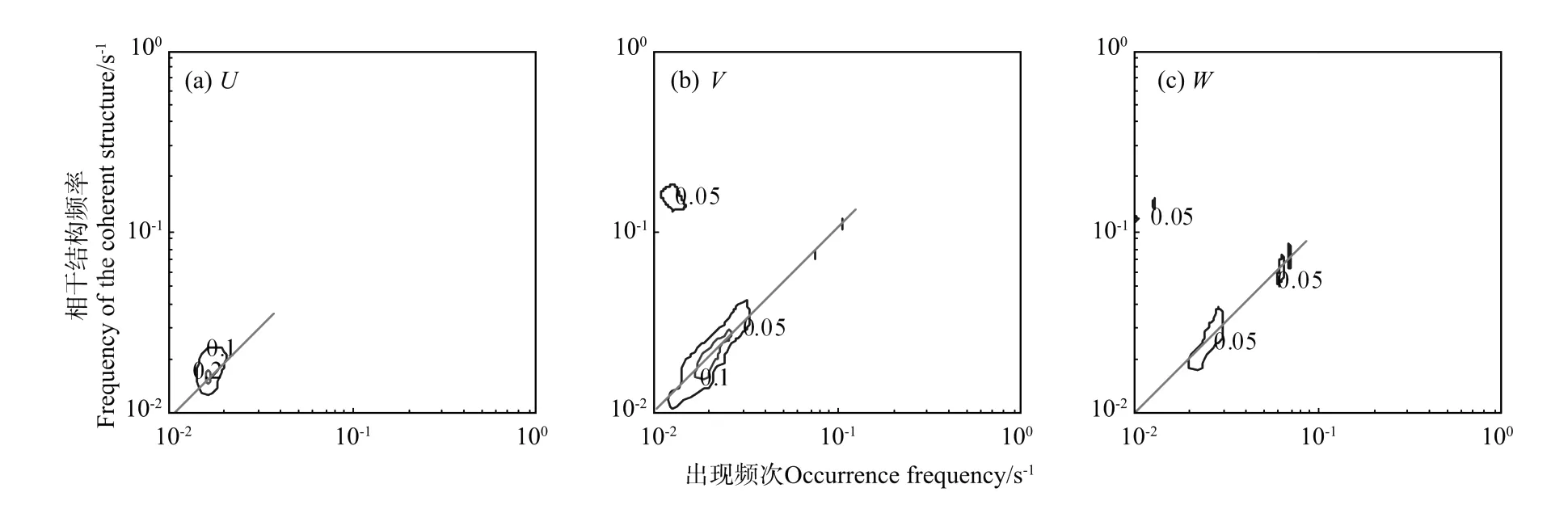
图7 小波系数谱分析图Fig.7 The spectral analysis of the wavelet coefficients
4 不同天气形势下相干涡结构特征
4.1 天气背景
选取2009年10月1日00∶00~2日00∶00 24 h的数据,在此时段内观测点受其南侧的热带气旋影响减弱,天气状况由阴雨逐渐转晴。
4.2 湍流特征
首先对原始资料按前面所述进行必要的预处理(去除野点,坐标旋转),然后对每0.5 h的数据进行统计分析,计算平均风速?U和脉动量u′、v′、w′及T′,并根据公式求得摩擦速度u*、Monin-Obukhov长度L、湍流强度Ij、风速标准差σj/u*(j=u,v,w)以及感热通量H0等湍流特征量。其中
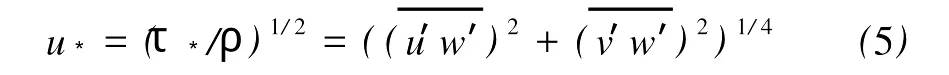
式中,ρ为空气密度,τ*为地表湍流摩擦阻力和分别为u和v方向的湍流通量。
Monin-Obukhov长度L,即大气层结稳定度参数由下式给出,

式中,g=9.8 m/s2为重力加速度,k=0.4为von Karman常数,T代表平均参考温度。
湍流强度定义为
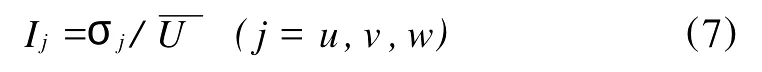
式中,σj为湍流风脉动的均方差。
感热通量计算公式为

其中,Cp是空气的定压比热。
表1给出了2009年10月1日00∶00~2日00∶00气象要素及湍流特征量的统计特征。
表1所示时段内,平均风速由约10 m/s逐渐减小并存在剧烈波动;摩擦速度与平均风速相对应,整体减小,证明海上摩擦速度和风速有较好的一致性;大气层结由一致的不稳定层结经过波动转变为稳定层结状态;湍流强度变化规律不明显,12∶00之后各方向湍流强度变化增加,水平方向有增强趋势,垂向上略有减弱后增强;感热通量整体减小,并变为负值。
湍流特征量的变化特征与观测点经历的天气过程具有较好的一致性。10月1日凌晨,观测点处于阴雨天气,对应不稳定层结状态,风速较大且稳定,相应的各方向上湍流强度也维持在一定范围内,感热通量为正,热量由海面向上输送。午后天气形势发生变化,在天气逐渐转晴的过程中,大气层结稳定度发生较大波动,在下午时段整体上保持不稳定层结状态,而夜间转为稳定层结。随着由对流天气转为平稳天气形势,平均风速减小,海面摩擦速度减小。与平均风速相对应,水平湍强增加,垂直方向上则受大气层结影响湍强略减后有所加强。感热通量随着对流减弱整体减小并表现出较大的波动,夜间转为负值,说明此时热量由大气向海洋传输。
4.3 相干结构特征分析
对30 min风脉动的小波能谱进行统计分析,考察1天内不同天气形势下相干结构能量分布及其随时间变化特征。垂直方向相干结构的尺度小于水平方向,且垂向小波谱的量值小于水平方向,说明垂向风脉动相干结构的尺度及能量小于水平分量,然而相干结构能量随时间的变化在3个风速分量上一致,垂直方向能量的大值往往与水平方向大尺度涡旋相对应。
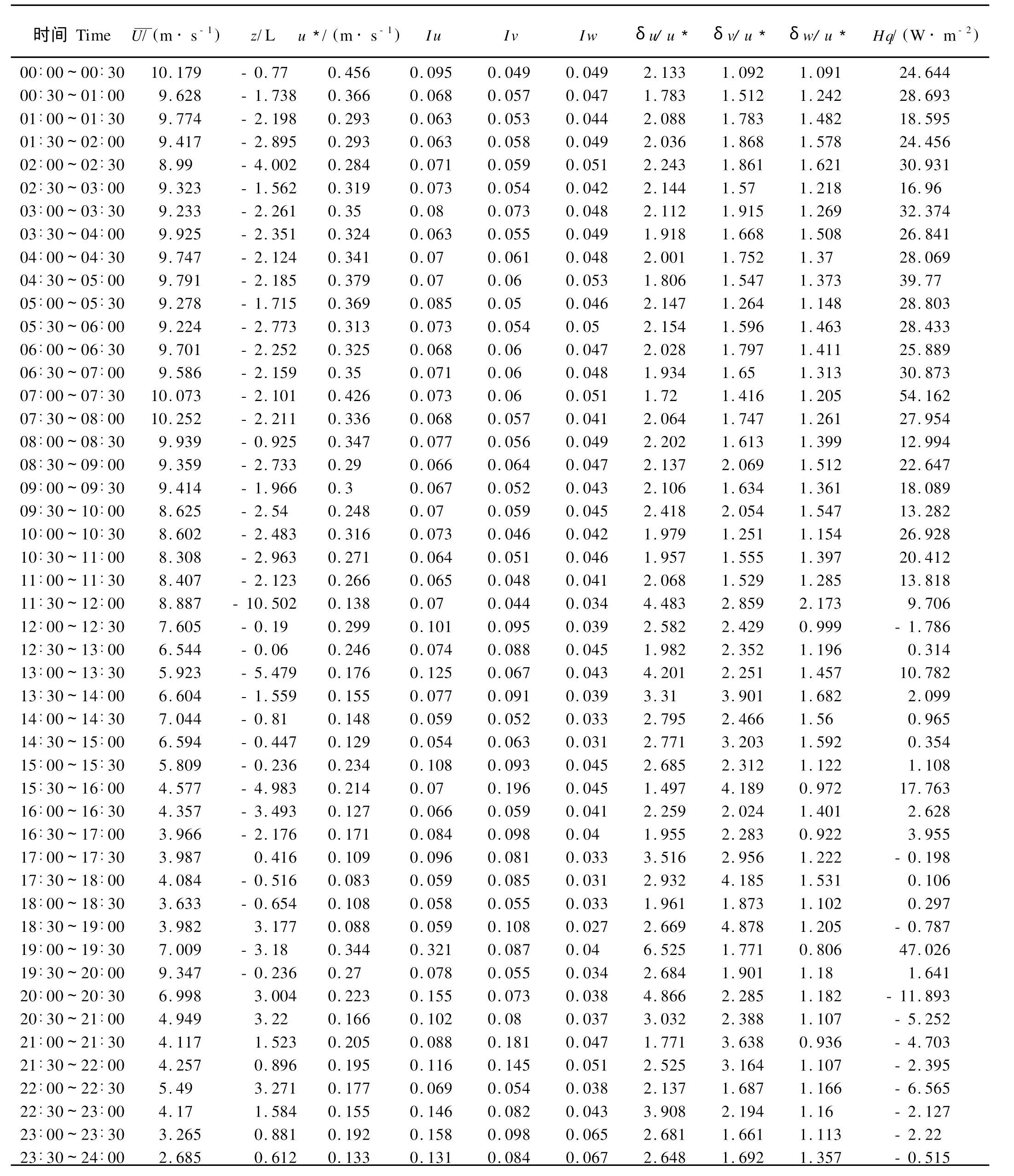
表1 2009年10月1日00∶00~2日00∶00气象要素及湍流特征量统计特征Table 1 Themeteorological element and characteristic value of turbulence from Oct.1 to Oct.2,2009
受文章篇幅的限制,这里仅给出了垂向风脉动的小波谱(见图8),横轴为时间轴,时间以0.5 h为间隔,纵轴用频率表征相干结构的尺度,图中色标给出了垂直风脉动小波谱的量值。从图中可以看到,垂直方向能量最大值所对应涡旋结构的尺度从几秒到几百秒不等,其中几十秒尺度的相干涡居多。不同天气条件下相干结构能量分布表现出不同的特征,阴雨对流天气小波谱能量大值区呈均匀带状分布,随着天气转晴,小波谱量值减弱且能量大值不连贯出现,说明相干结构的生成及能量分布与水平流场关系密切。阴雨天气对应不稳定层结条件,对流交换促使不同尺度上涡旋结构被充分激发,湍流充分发展;晴天,尤其是夜间稳定层结条件下,湍流发展被抑制,间歇性强,能量在尺度上分布较对流天气集中,相干结构不连续分布,涡旋能量低于对流天气。
总之,小波能谱能够很好的解释与天气形势相对应的湍流涡旋能量结构特征,它所刻画的相干结构并没有表现出明显的昼夜变化,特别是对于阴雨对流天气,能量分布均匀稳定与水平流场相联系,所以在分析大气湍流中相干结构时有必要结合相应的天气要素场的观测。
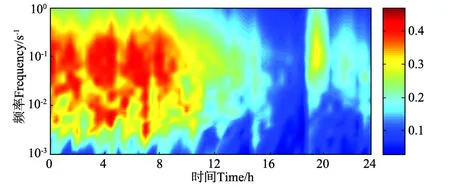
图8 2009年10月1日垂直风脉动小波能谱Fig.8 Wavelet energy spectrum of vertical velocity fluctuations of Oct.1,2009
5 结论
本文利用连续小波变换和谱分析的方法对南海近海塔测湍流风脉动资料进行分析,提取湍流相干结构,并结合相干结构的周期考察其生成和变化规律。通过分析不同天气条件下湍流统计量以及小波谱,探讨相干涡结构特征及其与典型天气形势之间的联系。
(1)利用小波变换提取的拟周期结构能够在数值和波形上很好地反映湍流信号的主要特征,体现了湍流中客观存在的某种中间尺度的相干涡旋。
(2)南海近海平坦下垫面湍流风速脉动存在几十秒主导尺度的相干结构,并表现出多尺度的特性。
(3)在一定的频段范围内,大气湍流风速相干结构主要以连续的方式生成,但较小尺度上的相干结构存在明显的不连续。
(4)大气湍流相干结构的生成和发展与天气形势,尤其是大气稳定度密切相关。阴雨对流不稳定层结条件下,湍流充分发展,涡旋强度大,尺度分布广;晴天夜间稳定层结条件下,湍流发展不充分,间歇性强,涡旋强度小,能量在尺度上分布相对集中,相干结构在时间上分布较为离散。
致谢:中国气象局广州热带海洋气象研究所为本文的工作提供了湍流数据,特此致谢。
[1] 邱翔,刘宇陆.湍流的相干结构[J].自然杂志,2004,26(4):187-193.
[2] 全利红,胡非,程雪玲.用小波系数谱方法分析湍流湿度脉动的相干结构[J].大气科学,2007,31(1):57-63.
[3] 刘海峰,汪海,于遵宏.小波分析及其在湍流研究中的应用[J].南昌大学学报,2000,22(4):43-50.
[4] 张斌,王彤,谷传纲,等.基于小波和双谱分析的湍流相干结构辨识[J].农业机械学报,2009,40(11):203-207.
[5] Farge M.Wavelet transforms and their applications to turbulence[J].Ann Rev Fluid Mech,1992,24:395-457.
[6] Gamage N,Hagelberg C.Detection and analysis of microfronts and associated coherent events using localized transforms[J].JA tmos Soc,1993,50:750-756.
[7] Gao W,Li B L.Wavelet analysis of coherent structures at the atmosphere-forest interface[J].Appl Meteor,1993,32:1717-1725.
[8] Coulter R L,LiB L.A technique using the wavelet transform to identify and isolate coherent structures in the planetary boundary layer,11th Symposium on Boundary Layer and Turbulence[C].Charlotte,NC:AMS,1995:291-294.
[9] 汪健生,尚晓东,舒玮.湍流信号的三项分解[J].力学学报,1997,29(5):519-524.
[10] 刘海峰,吴韬,王辅臣,等.应用小波分析研究湍流相干结构(Ⅰ)小波分析辨识相干结构的能量最大准则[J].化工学报,2000,51(6):761-765.
[11] Staszew ski W J,Worden K.Wavelet analysis of time-series;coherent structure,chaos and noise[J].International J of Bifurcation and Chaos,1999,9(3):455-471.
[12] 马耀明,王介民,刘巍,等.南沙海域近海层大气湍流结构及输送特征研究[J].大气科学,1997,21(3):357-365.
[13] 闰俊岳,姚华栋,李江龙,等.1998年南海季风爆发期间近海面层大气湍流结构和通量输送的观测研究[J].气候与环境研究,2000,5(4):447-458.
[14] 姜楠,王振东,舒玮.子波分析辨识壁湍流猝发事件的能量最大准则[J].力学学报,1997,20(4):406-411.
[15] 李春,何洪林,刘敏,等.China FLUX CO2通量数据处理系统与应用[J].地球信息科学,2008,10(5):557-565.
[16] 高会旺,顾明,王仁磊,等.北黄海海域大气湍流强度特征及风速标准差相似性分析[J].中国海洋大学学报:自然科学版,2009,39(4):563-568.
[17] 于贵瑞,陈晓敏.陆地生态系统通量观测的原理与方法[M].北京:高等教育出版社,2006:214-216.
[18] 王文圣,丁晶,李跃清.水文小波分析[M].北京:化学工业出版社,2005:24.
[19] 陈炯,郑永光,胡非.用连续子波变换提取城市冠层大气湍流的相干结构[J].大气科学,2003,27(2):182-190.
[20] Li Xin,Hu Fei,Pu Yifen,et al.Identification of coherent structures of turbulence at the atmospheric surface layer[J].Advances in A tmospheric Sciences,2002,19(4):687-698.
[21] 胡非.大气边界层湍流涡旋结构的小波分解[J].气候与环境研究,1998,3(2):97-105.
[22] Petenko IV,Bezverkhnii V A.Temporal scales of convective co-herent structures derived from sodar data[J].Meteorol Atmos Phys,1999,71:105-116.
[23] Petenko IV.Advanced combination of spectral and wavelet analysis(’spavelet’analysis)[J].Boundary-Layer Meteor,2001,100:287-299.
