深海吸力锚水平极限承载力研究*

张其一,董 胜,王青华

(1.中国海洋大学工程学院,山东青岛266100;2.青岛农业大学建筑工程学院,山东青岛266109;3.即墨房产管理局,山东青岛266200)

随着海洋石油工业逐渐向深海和超深海水域发展,张力腿平台(TLP)、立柱式(Spar)、船形浮式系统(FPSO)、顺应塔和半潜式平台等新型海洋结构及基础在工程中得到了广泛应用[1]。与浅海平台相比,这些深水平台的系锚荷载显著增加,竖向荷载不再是向下的压力,而是上拔荷载,并且海床土体的极限承载能力多以水平向为主,因此新型深海平台基础的承载特性及其计算方法,是深水海洋工程建设与设计中的关键技术问题[2]。

但是由于吸力式基础的应用历史较短,目前对于吸力式基础尚缺乏设计规范或统一标准。对于荷载作用下吸力式基础的承载力特性,通常基于一定的假设,采用极限平衡方法或极限分析方法进行简化分析。王志等人对Spar平台下的吸力式桶形基础进行了数值模拟,给出桶形基础极限承载力与加载点之间的关系,但是没有给出海床土体的破坏模式[3]。张建红等人在土工离心机上对桶形基础抗拔承载力进行了试验分析,认为深入研究桶形基础的承载机理具有很大的必要性[4],同时对水平荷载作用下张力腿平台吸力式基础承载特性进行了物理模型研究[5]。国振等人对准静力情况下吸力锚的极限承载力进行了研究分析,假定锚壁与海床土体之间不可分离,认为接触面上不存在拉应力,这一假定导致长径比较大的吸力锚失稳模式与工程实际有较大差别[6]。吴梦喜等人对吸力式沉箱的水平极限承载力进行了数值分析,认为系泊点位置决定了沉箱的失稳模式,并给出了沉箱失稳时的2种运动型式,但是没有对海床土体失稳机理进行理论研究,也没有给出沉箱具体的失稳破坏模式[7]。

为了深入探讨吸力式基础的破坏模式和极限承载力,本文基于有限元数值方法,在位移加载模式与前人研究结果的基础上[8-9],以吸力锚基础的水平极限承载力为研究目标,对吸力锚在水平载荷作用下的稳定性进行了数值分析。深海吸力锚基础模型见图1。

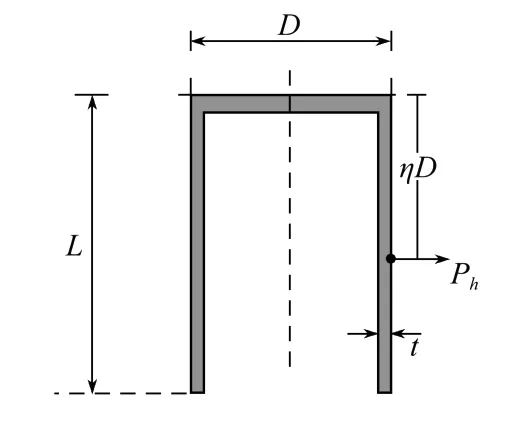
图1 吸力锚模型Fig.1 Model of suction anchor

图1中,Ph为吸力锚上所受到的水平系泊载荷;D与L分别为吸力式基础的直径和高度;η的大小决定了系泊点距离吸力锚顶部的距离。

1 数值分析

1.1 数值计算模型

为了研究饱和不排水海床上吸力锚的极限承载力,本文采用图2所示的有限元模型。海床土体弹性模量与泊松比分别为E=5.8 M Pa,v=0.49。土体为理想弹塑性材料,服从Mohr-Coulomb屈服准则,并满足相关联流动法则,内摩擦角和黏聚力分别取为<=0和c=12 kPa。吸力锚结构采用厚度为0.035 m的Q235钢,屈服强度取为215 M Pa,弹性模量取为1 500 M Pa,泊松比取为0.125。

在数值分析过程中,有限元模型包括2部分:吸力锚基础与饱和不排水软黏土海床。为了深入研究吸力锚基础失稳模式与海床土体破坏机理,本文以二维平面应变情况进行考虑,来分析土体的塑性变形规律。为了降低模型边界对数值计算精度的影响,饱和不排水软黏土海床长度取为20 D,深度取为10 L,采用8节点矩形平面单元(CPE8R)。由于不排水情况下饱和软黏土具有体积不可压缩的特性[10],使得基础极限承载力的求解实际上是1个具有齐次约束的非线性边值问题,在有限元数值计算过程中通常会造成“自锁现象”,故本文计算过程中采用了二阶减缩积分单元。计算结果表明,二阶减缩积分单元具有较快的收敛速度与较高的计算精度。另外,数值分析过程中为了能够合理模拟桶壁与海床土体的分离现象,吸力锚桶壁与海床土体之间的相互作用采用Coulomb摩擦对来模拟,接触面法向采用硬接触,切向采用罚函数法来定义摩擦特性,即桶壁摩擦力与桶壁所受到的垂向压应力成正比,桶壁与海床土之间不能承受拉力,当拉应力为零时桶壁与土颗粒分离。

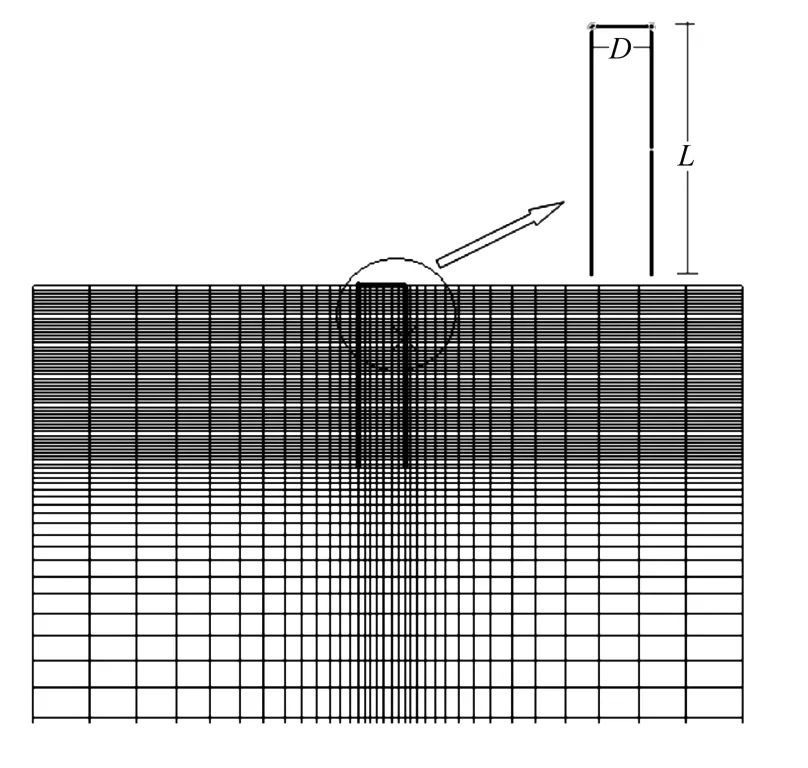
图2 有限元计算模型Fig.2 Finite element analysismodel

1.2 加载模式

在利用有限元进行数值计算的过程中,一般采用荷载控制方法或位移控制方法进行加载。与荷载控制方法相比,位移控制方法能够较准确地求得基础的荷载-位移曲线[11]。当荷载-位移曲线的斜率接近0时,意味着荷载不变情况下基础的位移也会持续地增大,因而可以确定此时地基达到了极限平衡状态,与极限平衡状态所对应的基础荷载就是地基的极限承载力。图3给出了利用位移加载模式,求解二维条形基础竖向极限承载力过程中的载荷-位移变化关系。

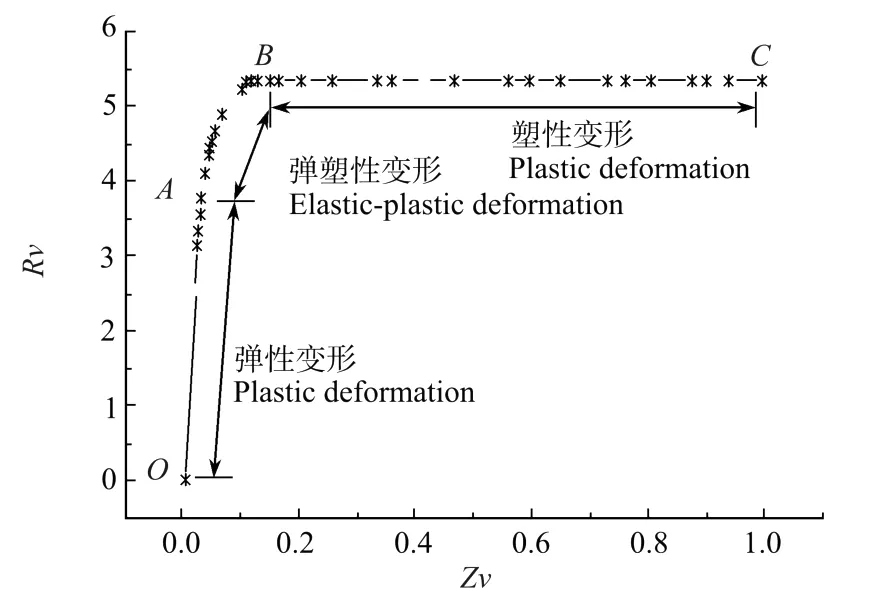
图3 位移-载荷关系曲线Fig.3 Settlement and loading of rectangular footing

图3所示的位移-载荷关系曲线表明,在利用位移控制法求解极限平衡问题的极限载荷时,变形通常会出现3个阶段,即弹性变形阶段、弹塑性变形阶段和塑性大变形阶段。OA阶段为弹性变形阶段,此时海床土体未产生不可恢复的塑性变形;AB阶段为弹塑性非线性变形阶段,AB阶段斜率逐渐由陡变缓,表明海床中局部土体开始达到塑性平衡状态,并且塑性平衡区域随着荷载的逐渐增加而进一步扩大;BC阶段为塑性大变形阶段,该阶段曲线斜率进一步平缓,斜率近似为0,即在荷载不变的情况下位移沿受荷方向持续增大,表明海床土体塑性区域已经贯通,此时海床土体发生破坏,吸力锚失去稳定性。

2 数值计算结果

2.1 极限承载力

为了详细研究吸力锚在水平系泊载荷情况下的水平极限承载力Ph,本文分别针对L=2 D、3 D、4 D、,5 D,以及系泊点在泥面以下0.0 D、0.5 D、1.0 D、1.5 D、2.0 D、2.5 D、3.0 D、3.5 D、4.0 D、4.5 D、5.0 D等情况进行数值分析,即η分别取0.0、0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0。计算结果见图4。

在土体极限平衡定理的基础上,由图4计算结果可知:对于吸力锚而言,随着系泊点位置η的变化,不排水海床地基提供给吸力锚的水平极限承载力Ph相继发生变化,吸力锚极限水平荷载Ph随系泊点η的增加,呈现先增大后减小趋势,对于吸力锚基础而言,系泊点η存在一个最理想的临界位置,系泊点处于临界位置时,吸力锚能够提供最大的水平极限承载力Phmax。由土压力平衡理论可知,吸力锚达到塑性极限平衡状态时,随着系泊点η位置的变化,吸力锚本身会呈现不同的失稳模式,海床土体破坏机理也会发生相应变化。

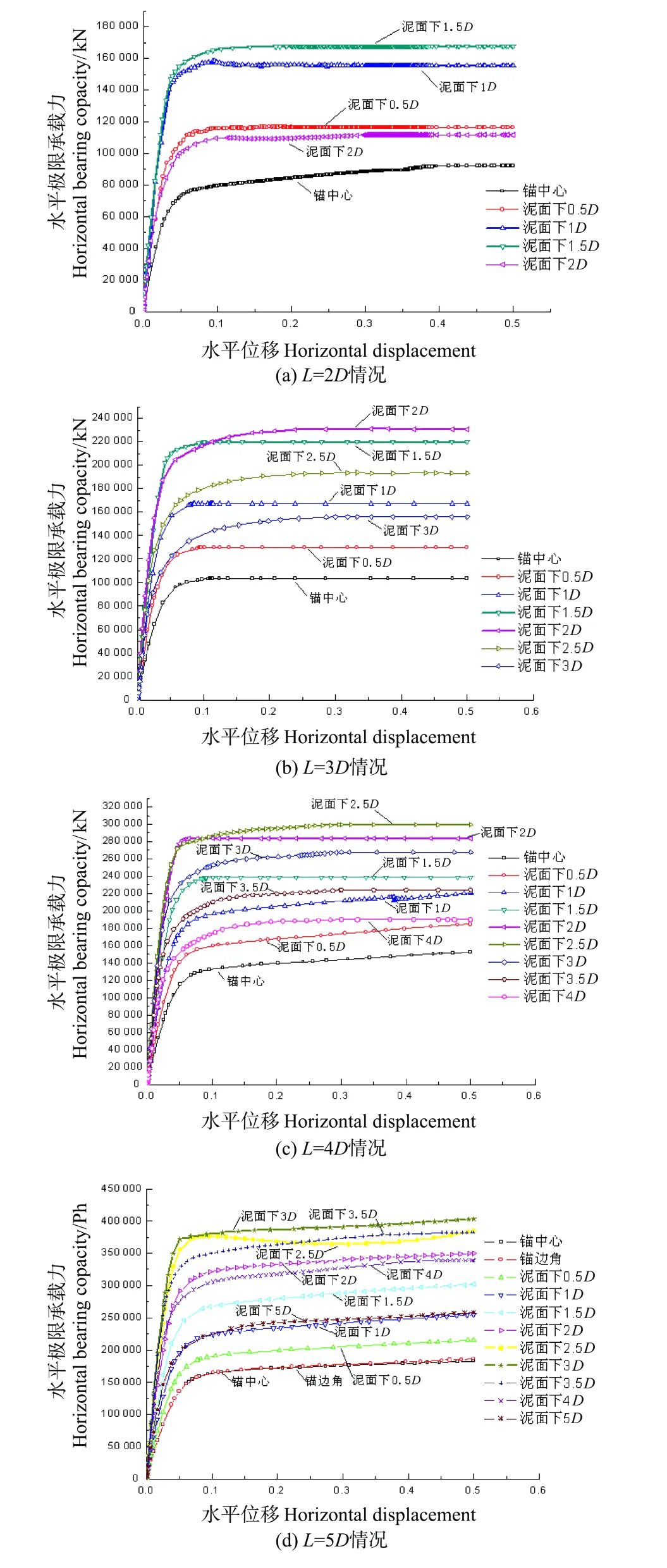
图4 不同系泊点处的水平极限承载力Fig.4 Horizontal ultimate bearing capacity with different mooring points

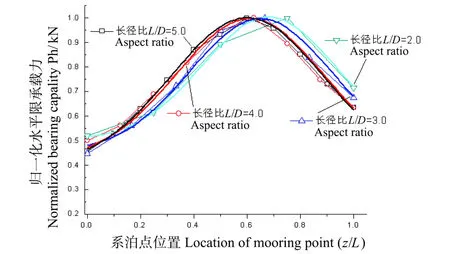
图5 吸力锚极限承载力同系泊点对应关系Fig.5 Relationship between bearing capacity and moo ring point of suction ancho r

由图5所示的吸力锚极限承载力与系泊点关系曲线可知:(1)当系泊点位于吸力锚封闭顶板上时,吸力锚能够承载的水平极限承载力Ph最小,约为吸力锚最大水平极限承载力Phmax的45%～55%,此时吸力锚将沿着加载方向发生向前倾覆转动,本文称其为前倾转动;(2)随着系泊点η的逐渐增大,吸力锚所能承受的最大水平荷载Ph相继增大,当系泊点η增大到某一临界深度时,吸力锚所能承受的水平载荷Ph最大,此时吸力锚将沿着加载方向平移,本文称其为平移滑动;(3)随着系泊点η的进一步增大,吸力锚所能承受的水平极限荷载Ph将逐渐降低,吸力锚沿着加载方向发生向后倾覆转动,本文称其为后仰转动,此时吸力锚的极限承载力Ph仍比系泊点在锚顶位置时大;(4)随着吸力锚长径比L/D的逐渐增大,吸力锚最优系泊点位置逐渐上移,最优系泊点位置介于(0.6～0.75)之间。

考虑到实际工程中吸力锚长径比L/D一般<10,在上述计算结果的基础上,本文给出了深海吸力锚极限承载力Ph与系泊点位置之间的简易表达式:

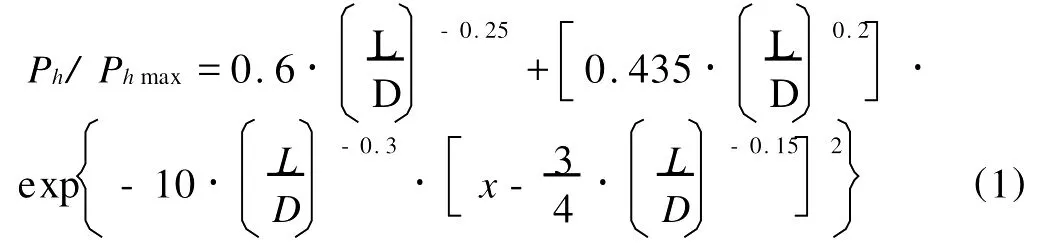
式中,x表示系泊点与桶顶的相对距离,Ph为对于不同系泊点而言吸力锚所具有的水平极限承载力,Phmax为系泊点处于临界状态时海床土体提供给吸力锚的最大极限承载力,L/D为吸力锚长径比。

2.2 失稳破坏模式

在对吸力锚水平极限承载力Ph进行数值研究过程中,本文对吸力锚失稳形式和海床土体破坏模式进行了分析,根据吸力锚的失稳机理,分别提出了前倾转动、平移滑动和后仰转动失稳模式。不同长径比与系泊点情况下吸力锚达到塑性极限平衡状态时,海床土体的位移云图见图6～8。

图6表明当吸力锚系泊点作用在桶顶处,吸力锚失稳时发生前倾转动破坏。沿着加载方向吸力锚上部桶体压缩土体,使得上部土体呈现被动破坏,从而导致吸力锚上部桶体部分受到被动土压力作用;沿着加载方向吸力锚下部桶体绕某一转动中心旋转,转动中心以下土体发生主动破坏,从而使得吸力锚此处承受主动土压力作用。吸力锚背面的上部桶壁与土体之间出现拉应力,桶壁与土体分离,此处吸力锚不受荷载作用;吸力锚背面的下部土体,由于该处锚体运动型式以转动为主,所以此处土体呈现被动破坏,对桶壁产生被动土压力。

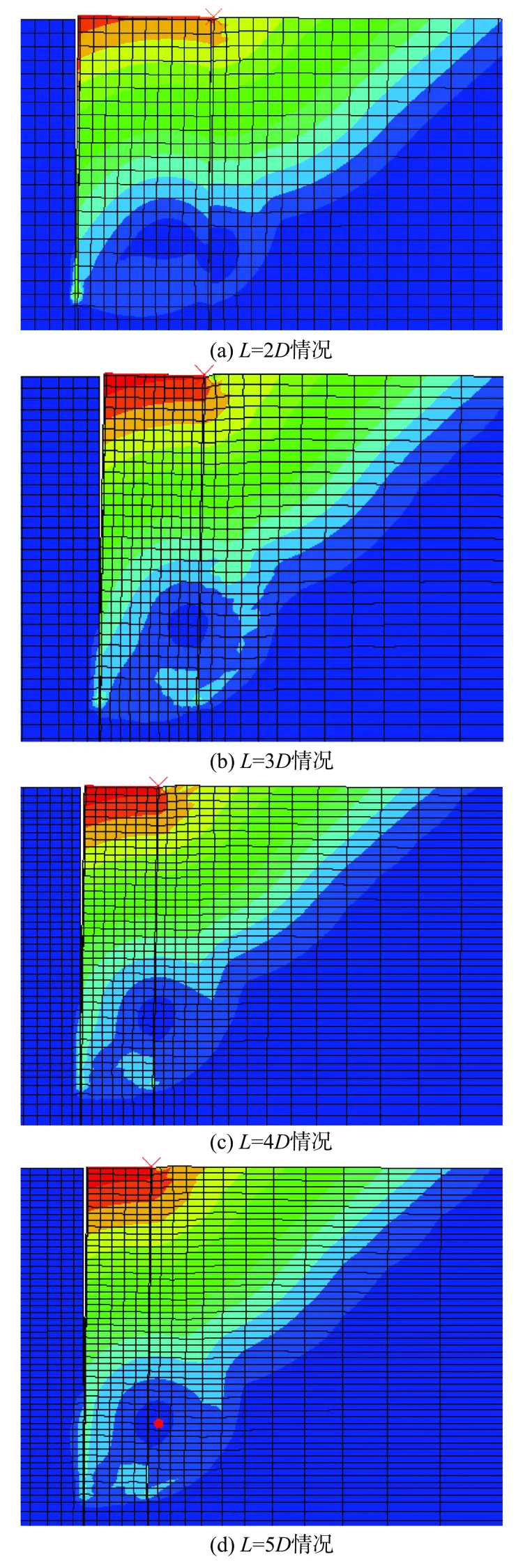
图6 系泊点η=0位置对应的破坏模式Fig.6 Failure mode of soil with moo ring pointη=0

图6(a)所示的吸力锚破坏模式表明,海床土体发生旋转破坏时转动中心位于桶内的下部某一位置,桶内土体的旋转现象不是十分明显,此时桶壁与桶内土体之间的摩擦约束较弱;(b)～(d)所示的破坏模式表明,随着吸力锚长径比的逐渐增大,桶体下部土体的转动现象变得明显,当长径比L/D<4时,桶内壁与桶内土体之间的摩擦作用比较明显,土体转动中心被约束在桶内部,当长径比L/D>4时,桶外壁对桶外土体的摩擦作用逐渐强过桶内壁对桶内土体的摩擦作用,此时吸力锚下部土体的转动中心外移,位于桶壁外部。

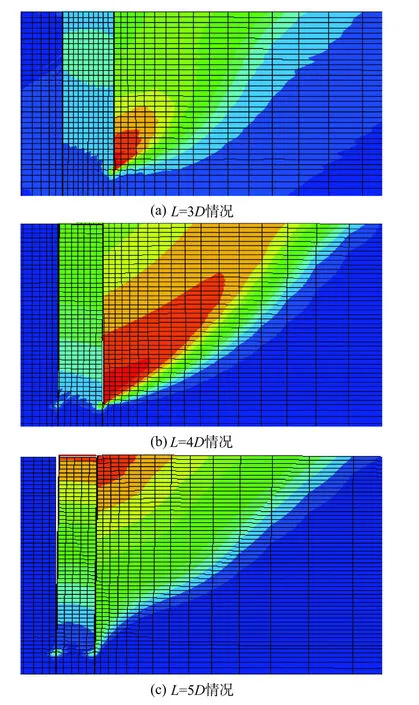
图7 系泊点η=2.5位置对应的破坏模式Fig.7 Failuremode of soil with mooring pointη=2.5

图7表明当吸力锚系泊点较深时,吸力锚失稳时发生平移滑动破坏。沿着加载方向吸力锚整体压缩土体,使得土体整体呈现被动破坏,从而导致吸力锚整体受到被动土压力作用。

图7(a)～(b)所示的吸力锚破坏模式表明,海床土体发生平移滑动破坏时,由于吸力锚长径比较小,桶外壁与海床土体之间的摩擦作用较小,较小的摩擦力对桶端土体约束作用较弱,此时在桶壁的平移运动下,桶底土体首先达到塑性平衡状态,随着系泊点水平荷载Ph的进一步增加,塑性区逐渐向海床表面扩张;(c)所示的破坏模式表明,随着长径比的逐渐增大,桶底外侧与海床土体之间的摩擦力也逐渐增加,较大的摩擦作用使得桶端土体塑性区受到较大的约束作用,从而导致桶端土体初始破坏角较小,导致破坏滑裂面出现图中所示的双圆弧形状;事实上,海床土体发生破坏时滑裂面形状应该为平面或对数滑裂面,由于本文未考虑摩擦角的影响,使得对数滑裂面退化为圆弧滑裂面。

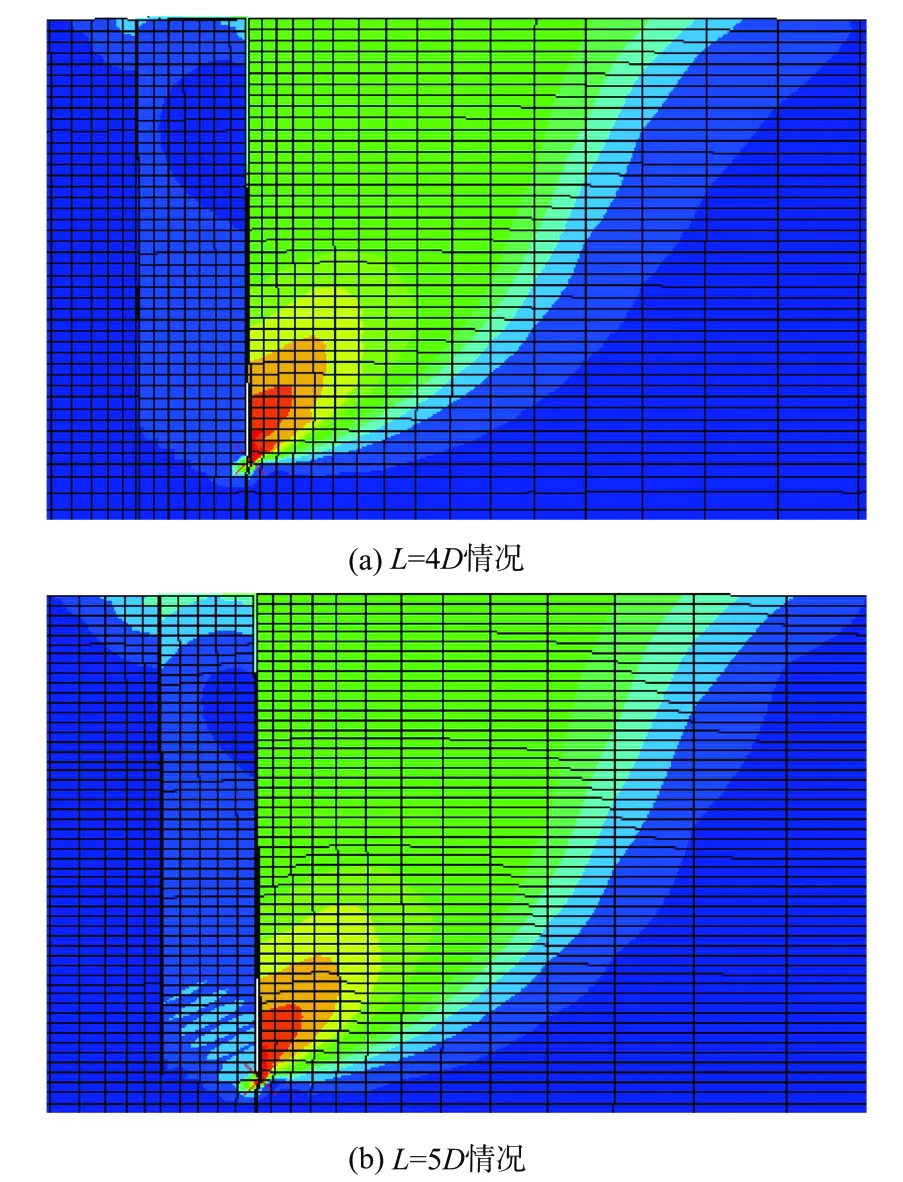
图8 系泊点η=4位置对应的破坏模式Fig.8 Failure mode of soil with moo ring pointη=4

图8表明当吸力锚系泊点处于锚底附近时,吸力锚失稳时发生后仰转动破坏。沿着加载方向吸力锚以锚顶某一位置为转动中心整体压缩土体,使得土体呈现被动破坏,从而导致吸力锚受到被动土压力作用。

图8(a)～(b)所示的吸力锚破坏模式表明,吸力锚发生后仰转动破坏时,随着吸力锚长径比的逐渐增加,吸力锚桶壁后侧的被动土压力区域逐渐加深并扩大,所提供给桶壁的被动土压力相继增大,同时桶体内部土体的转动中心逐渐向桶壁靠近,从而使得桶内土体与桶体内壁之间的摩擦效应更加显著。

由本文的有限元数值计算结果,针对吸力锚桶壁两侧土体破坏模式,可以进一步给出如下推论:(1)随着吸力锚长径比的进一步增大,系泊点一侧与桶壁相接触的海床土体发生破坏时,破坏滑裂面(或速度不连续边界)将不再是单一的滑弧,即滑弧出溢点将会终结于海床某一深度范围内;(2)吸力锚桶体内部土体与桶壁的相互作用,会明显提高吸力锚极限承载能力,作用机理同土骨架力学特性、孔隙水的渗透性质、锚自身的长径比等因素有关。本文得出的推论,将在另外一篇文章中详细阐述。

3 结论

在本文给出的数值模型基础上,基于极限平衡原理利用有限元分析软件ABAQUS,对深海吸力锚的水平极限承载力进行了数值分析,得出如下结论:

(1)本文给出的数值模型,能够较为准确地求解深海吸力锚的水平极限承载力,并能够对吸力锚的稳定性进行合理评估。

(2)吸力锚的极限承载力及其稳定性,受系泊点位置、锚自身的长径比等因素影响较大;当系泊点位置在吸力锚入泥深度范围内,更能发挥深海吸力锚的承载能力。

(3)本文给出的吸力锚水平极限承载力计算公式(1),能够较为合理地评估系泊点位置、长径比对吸力锚极限承载力的影响。

(4)本文给出的前倾转动破坏模式、平移滑动破坏模式以及后仰转动破坏模式,较为合理地反映了系泊点位置对吸力锚稳定性的影响,为进一步利用解析法深入研究吸力锚的稳定性奠定了理论基础。

[1] 王志云,王栋,栾茂田,等.复合加载条件下吸力式沉箱基础承载特性数值分析[J].海洋工程,2007,25(2):52-71.

[2] 鲁晓兵,矫滨田,刘亮.饱和砂土中桶形基础承载力的试验研究[J].岩土工程技术,2006,20(4):170-173.

[3] 王志,杜守继,王德禹.Spar平台吸力式基础极限承载特性数值分析[J].海洋工程,2009,27(3):54-75.

[4] 张建红,孙国亮.海洋平台吸力式基础的土工离心模拟研究与分析[J].海洋工程,2004,22(2):90-97.

[5] 张建红,林小静,鲁晓兵.水平荷载作用下张力腿平台吸力式基础的物理模拟[J].岩土工程学报,2007,29(1):77-81.

[6] 国振,王立忠.吸力锚基础锚泊线准静力分析模型[J].海洋工程,2009,27(4):1-9.

[7] 吴梦喜,王梅,楼志刚.吸力式沉箱的水平极限承载力计算[J].中国海洋平台,2001,16(4):12-15.

[8] 栾茂田,赵少飞,袁凡凡.复合加载模式作用下地基承载性能的数值分析[J].海洋工程,2006,24(1):34-40.

[9] 张其一,栾茂田,赵少飞,等.复合加载模式下条形基础承载力下限分析[J].中国矿业大学学报,2008,37(3):364-368.

[10] Merifield R S,Nguyen V Q.Two-and three-dimensional bearing-capacity solutions for footingson two-layered clays[J].Journal of Geomechanics and Geoengineering.2006,1(2):151-162.

[11] 栾茂田,张其一,杨庆,等.均质地基上浅埋矩形基础极限承载力上限分析[J].海洋工程,2008,26(2):69-77.