曲线最小二乘拟合的自适应方法

周 俊

（长江大学 信息与数学学院，湖北 荆州 434023）

曲线最小二乘拟合的自适应方法

周 俊

（长江大学 信息与数学学院，湖北 荆州 434023）

文章提出了一种自适应的最小二乘曲线拟合方法.根据观测数据该方法自适应地选择拟合函数模型.数值结果表明，所提出的自适应方法能更好地拟合观测数据之间的关系.

曲线拟合；最小二乘；自适应方法；函数模型

0 引言

科学研究与工程计算中，常常需要从一组观测数据｛（x i，y i），i＝1，2，…，m｝出发，寻找变量x，y的函数关系式y＝f（x）.绝大多数情况下很难找到它们之间的精确表达式，这时就要根据观察点，利用最小二乘曲线拟合去构造一个近似解析式y＝f（x）≈F（C，x）.利用该方法拟合出的函数曲线虽然不能保证通过所有的样本点，但是很好地逼近了它们，充分反映了已知数据间内在的数量关系，在实践中具有广泛的应用前景［1］.

最小二乘曲线拟合的关键是选择曲线拟合函数

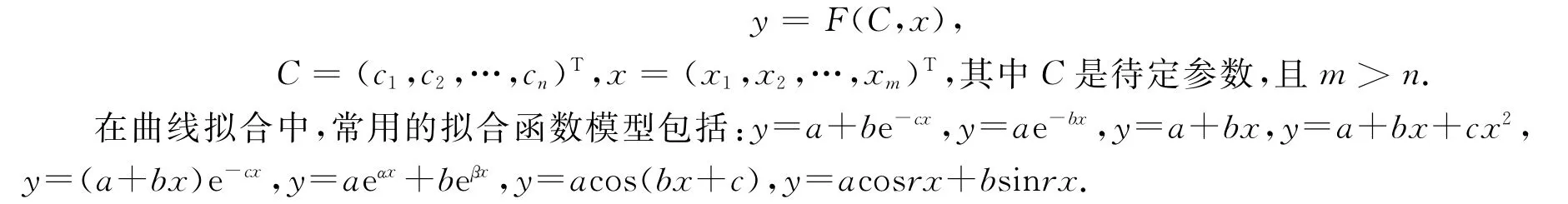
现有的曲线拟合方法大多数是根据观测数据的分布状况来选取相应的拟合函数模型，有时所选定的拟合函数模型并不能准确地反映出数据间的关系.因此如何根据数据的总体分布状况，减少主观影响因素，选取恰当的拟合函数模型越来越受到研究者的重视.

在本文中，我们将提出一种自适应最小二乘曲线拟合方法，即根据观测数据自适应地选择恰当的拟合函数模型.方法减少了人为因素，能够恰当地拟合观测数据之间的关系.数值结果表明，相比于传统拟合方法，自适应拟合方法能更好地反映数据间的关系.

1 自适应方法

根据观测数据，不妨假设拟合函数模型具有如下形式：

考虑到常微分方程基础解系能够包含多种简单函数形式，因此将拟合基函数Φ1（x），Φ2（x），…，Φn（x），视为如下常微分方程

的基础解系，并且满足节点函数条件，即y1＝F（x1），…，y m＝F（x m）.

对于常微分方程（2）系数的确定，可以由观测数据y1，y2，…，y m（m＞n）确定，这就是所谓的常微分方程的反问题［2］：

通过求解常微分方程中的系数a0，a1，…，an－1，得出拟合基函数Φ1（x），Φ2（x），…，Φn（x），最后采用最小二乘法，得到拟合函数模型.

2 计算方法

3 数值试验

为了说明自适应拟合方法的优越性，本节我们对观测数据（表1）采用自适应法选择拟合模型，确定y与x的关系.

表1 观测数据

算法1 求解y″＋βy′＋γy＝0，y（x r）＝f（x r），r＝1～10.利用式（7）确定常数β，γ，并求出拟合基函数Φ1（x），Φ2（x），再作最小二乘拟合，得到拟合函数为：

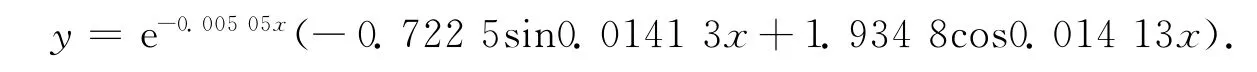
算法2 求解y″＋ay＝0，y（x r）＝f（x r），r＝1～10.利用式（6）求出基函数Φ1（x），Φ2（x），再作最小二乘拟合，得到拟合函数为［3］：

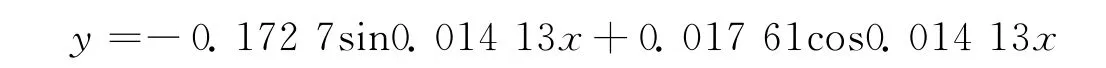
算法3 用y″＋ay＝0，y（x r）＝f（x r），r＝1～10.利用式（4）求出基函数Φ1（x），再作最小二乘拟合，得到拟合函数为［3］：

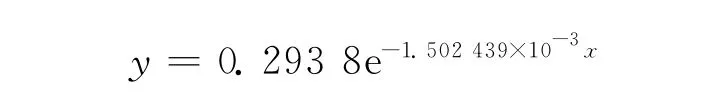
利用MATLAB画出三种算法得到的拟合函数对观测数据的拟合情况，从图1-a可以看出算法1效果最好，所以取拟合函数为：

此时残差平方和‖Y－y‖2＝0.003 4.

算法4 对数据y作自然对数变换，取对数U＝lny，再利用算法1，根据式（7）确定常数β，γ，并求出拟合基函数Φ1（x），Φ2（x），再作最小二乘拟合，得到拟合函数为［3］：

此时残差平方和‖Y－y‖2＝1.3×10－4，从图1-b中也可以看出，对数据作自然对数变换后得到的拟合函数，其拟合效果比算法1的效果更好.

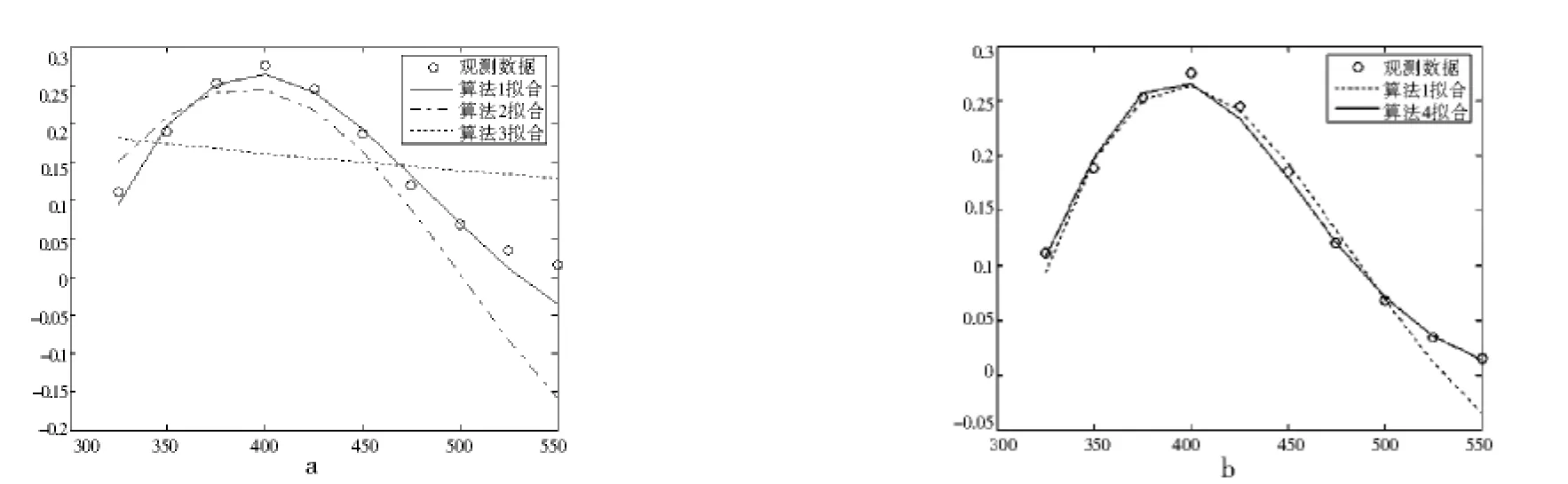
图1 观测数据与曲线拟合

4 结论

最小二乘曲线拟合就是一种揭示数据间内在联系的非常重要的方法，在数据处理和误差分析中应用非常广泛，可提高数据处理的效率和精确度.本文提出一种自适应的最小二乘曲线拟合方法，根据观测数据自适应选择拟合模型.数值结果表明，该方法能有效地反映数据间的联系.

［1］陈 忠，朱建伟.数值计算方法［M］.北京：石油工业出版社，2003

［2］东北师范大学微分方程教研室.常微分方程［M］.北京：高等教育出版社，2006

［3］薛定宇，陈阳泉.高等应用数学问题的MATLAB求解［M］.北京：清华大学出版社，2004

An Adaptive Least Square Method for Fitting Curve

Zhou Jun
（School of Information and Mathematics，Yangtze University，Jingzhou 434023，China）

An adaptive least square method for fitting curve is proposed.Following the observed datas，the method proposed can choose the fitting functions adaptively.The numerical results show that the adaptive method can fit the relationship among the observed datas perfectly.

fitting curve；least square；adaptive method；function model

王映苗】

1672-2027（2011）03-0017-04

O241.5

A

2011-03-25

湖北省教育厅A类重点项目（D20101304）.

周 俊（1975-），男，湖北天门人，硕士，长江大学信息与数学学院副教授，主要从事最优化理论方面的教学与研究.