可撤销的公钥加密方案的形式化分析

于瑞琴

（镇江高等专科学校电子信息系，江苏 镇江 212003）

可撤销的公钥加密方案的形式化分析

于瑞琴

（镇江高等专科学校电子信息系，江苏 镇江 212003）

通常的密码系统，IBE或者PKI都必须提供从系统中撤销用户私钥的途径，同样PEKS也应该提供撤销陷门的方式.本文研究了可高效撤销的无需安全信道的带关键字搜索公钥加密方案的形式化定义及安全模型.基于BDH问题，可证明方案的安全性.

带关键字公钥搜索加密；可撤销；双线性对；无需安全信道

0 引言

为了实现加密电子邮件智能路由，即第三方不需要解密密文就可以检测或者验证密文中是否含有某些关键字.Boneh等人［1］在2004年提出了带关键字搜索公钥加密方案，该方案的缺点是在接收者和邮件服务者之间需要一个安全信道来传送陷门，而这个开销往往是很昂贵的.为了解决这一缺点，Baek等人［2］提出了无需安全信道的带关键字搜索公钥加密方案.2007年，Gu等人［3］提出了一个更有效的基于双线性对的带关键字搜索公钥加密构造，然后他们进一步构造了随机预言模型下的无需安全信道的带关键字搜索公钥加密方案.为了避免使用随机预言机，最近Fang等人［4］构造了标准模型下的无需安全信道的带关键字搜索公钥加密方案.文献［5-8］研究了改进的带关键字搜索公钥加密方案，其中文献［5］提出了从任意的匿名IBE方案构造带关键字搜索公钥加密方案的一般化方法，反之亦然.

在IBE或者PKI系统中，如果用户的私钥泄露了，就必须提供从系统中撤销用户的途径.同样在带关键字搜索公钥加密中，接收者在发送出某关键字对应的陷门给服务者后，因为某种原因不想让服务者继续搜索相应关键字了，即想撤销这一关键字陷门是很自然的.本文研究了可高效撤销的无需安全信道的带关键字搜索公钥加密方案的形式化定义及安全模型.基于BDH问题，可证明方案的安全性.

1 背景知识

1.1 双线性对

定义1 双线性对（Bilinear pairings）［4］.

设G1、G2都是阶为素数p的乘法交换群，g是G1的产生元，如果以下三个条件成立，则e：G1×G1→G2是一个可计算的双线性对映射：（1）双映射性：对所有a，b∈Z，有e（g a，gb）＝e（g，g）ab；（2）非退化性：e（g，g）≠1；（3）可计算性：对于P，Q∈G1，可计算e（P，Q）.

1.2 可忽略函数

1.3 复杂性假设

定义3 BDH假设：

2 可撤销带关键字搜索公钥加密方案的形式化定义及安全模型

定义4 （R－SCF－PEKS）：可高效撤销的带关键字搜索的公钥加密方案包含下面几个算法，假设关键字域为KSw，时间段域为τ.

GloSetup（λ，n）：输入安全参数λ，实际关键字陷门数n∈N，输出公共参数GP.

Key Gensever（GP）：以公共参数GP为输入，输出服务者S的公钥对（pks，sks）.

Key Genreciver（GP）：以公共参数GP为输入，输出接收者R的公私钥对（pks，sk R），初始状态st，空的撤销列表RL.

KTrap door（GP，sk R，w）：由接收者运行，输入公共参数GP，接收者的私钥sk R，关键字w，状态st.产生初始陷门d w和更新的状态st.

UTrapdoor（GP，sk R，t，st，RL）：由接收者运行，输入公共参数GP，接收者的私钥sk R，更新陷门时间t∈τ，撤销列表RL，状态st.产生更新陷门ut.

Trap door（d w，ut）：输入关键字的初始陷门d w，更新陷门ut，输出在时间t的实时陷门T w，t.

PEKS（GP，pk R，w，t）：输入公共参数GP，接收者的公钥pk R，服务者的公钥pk S，关键字w∈KSw，时间t∈τ.返回一个用关键字w和时间t加密的PEKS密文C.

Test（GP，sk S，C，T w，t）：输入公共参数GP，服务者的私钥sk S，在时间t的实时陷门T w，t，PEKS密文C＝PEKS（GP，pk R，pk S，w′，t）.如果w＝w′，输出“正确”，否则输出“错误”.

Revocation（GP，w，t，RL，st）：由接收者运行，输入公共参数GP，将要撤销的关键字w，撤销时间t∈τ，撤销列表RL，状态st，输出更新的撤销列表RL.

接下来将给出基于游戏的安全性定义，称为可撤销的无需安全信道的抗选择关键字攻击不可区分性（IND－R－SCF－CKA）.

定义5 （IND－R－SCF－CKA游戏）：λ是安全参数，A是攻击者.考虑下面两个游戏：Gameserver：假设A是服务者.

1.系统建立：公共参数产生算法GloSetup（λ）和两个密钥产生算法Key Genreceiver（GP），Key Gensever（GP），被执行，产生公共参数GP，初始状态st，空的撤销列表RL，接收者和服务者的公私钥对（pk R，sk R），（pks，sks），接着模拟者B把（pk S，sk S）和pk R发送给攻击者A.

2.查询阶段1：攻击者A做了一系列的查询：

初始陷门查询〈w〉：A适应地询问B他所选择的关键字w，w∈KSw，所对应的初始陷门d w，B返回给A初始陷门d w＝KTrapdoor（GP，sk R，w）.

更新陷门查询〈t〉：A适应地询问B他所选择的时间段t所对应的更新陷门，B返回给A更新陷门u t＝UTrapdoor（GP，sk R，t，st，RL）.

撤销查询〈w，t〉：A对他所选的关键字w和时间t做撤销查询，执行Revocation（GP，w，t，RL，st）更新RL.

3.挑战：一旦A决定查询1阶段结束，他输出挑战关键字对（w0，w1）和挑战时间t＊.接收到挑战关键字对后，B随机地选择β∈｛0，1｝，并且产生挑战密文C＊＝PEKS（GP，pk R，pk S，wβ，t＊），发送给A.

4.查询阶段2：A做和阶段1相同的查询.

5.猜测：攻击者输出他的猜测β′，如果β＝β′，则攻击者获得胜利.

注意游戏必须遵循下面限制：

更新陷门查询〈t〉和撤销查询〈w，t〉允许对大于等于先前的时间查询，即攻击者只允许对非递减时间进行查询.同时，如果对时间t查询更新陷门查询〈t〉，则不允许对时间t查询撤销查询〈w，t〉.

如果对挑战关键字w i，i＝0，1，做初始陷门查询，则撤销查询〈w i，t〉的时间t必须满足t≤t＊.

1）系统建立：公共参数产生算法GloSetup（λ）和两个密钥产生算法Key Genreceiver（GP），Key Gensever（GP）被执行，产生公共参数GP，初始状态st，空的撤销列表RL，接收者和服务者的公私钥对（pk R，sk R），（pk S，sk S），接着模拟者B把（pk R，sk R）和pk S发送给攻击者A.

2）查询阶段1：攻击者A做一系列的查询：

初始陷门查询〈w〉：因为A知道接收者的私钥，他能够自己计算他所选择的关键字w，w∈KSw，所对应的初始陷门d w.

更新陷门查询〈t〉：因为A知道接收者的私钥，他能够自己计算他所选择的时间t，t∈τ，所对应的更新陷门ut.

撤销查询〈w，t〉：A对他所选的关键字w和时间t做撤销查询，执行Revocation（GP，w，t，RL，st）更新RL.

3）挑战：一旦A决定查询1阶段结束，他输出挑战关键字对（w0.w1）和挑战时间t＊.接收到挑战关键字对，B随机地选择β，其中β∈｛0，1｝，并且产生挑战密文C＊＝PEKS（GP，pk R，pk S，wβ，t＊），发送给A.

4）查询阶段2：A做和阶段1相同的查询.

5）猜测：攻击者输出他的猜测β′，如果β＝β′，则攻击者获得胜利.

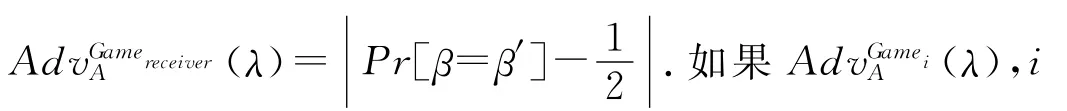
3 结论

本文给出了一个可高效撤销的无需安全信道的带关键字搜索公钥加密方案的形式化定义及安全模型，基于BDH假设，可以证明可高效撤销的无需安全信道的抗选择关键字攻击不可区分的安全性（IND-R-SCFCKA）.

［1］Boneh D，Crescenzo G Di，Ostrovsky R，et al.Public key encryption with keyword search［A］.In Proc.of EUROCRYPT 2004，LNCS 3027［G］.Heidelberg：Springer，2004：506-522

［2］Baek J，Safavi-Naini R，Susilo W.Public key encryption with keyword search revisited［A］.In Proc.of Applied Cryptography and Information Security 06（ACIS 2006），LNCS 5072［G］.Berlin：Springer-Verlag，2008：1 249-1 259

［3］Gu C，Zhu Y，Pan H.Efficient public key encryption with keyword search schemes from pairings［A］.In Proc.of Information Security and Cryptology：third SKLOIS conference，inscrypt 2007，LNCS 4990［G］.Heidelberg：Springer-Verlag，2007：372-383

［4］Fang L，Susilo W，Ge C，et al.A secure channel free public key encryption with keyword search scheme without random oracle［A］.In Proc.of cryptology and network security，8th International Conference，CANS 2009，LNCS 5888［G］.Heidelberg：Springer，2009：248-258

［5］Abdalla M，Bellare M，Catalano D，et al.Searchable encryption revisited：consistency properties，relation to anonymous IBE and extensions［A］.In Proc of CRYPTO 2005，LNCS 3621［G］.Berlin：Springer-Verlag，2005：205-222

［6］Rhee H S，Park J H，Susilo W，et al.Improved searchable public key encryption with designated tester［A］.In Proc.of the 4th international symposium on information，computer，and communications security（ASIACCS’09）［G］.New York：ACM，2009：376-379

［7］Rhee H S，Susilo W，Kim H-J.Secure searchable public key encryption scheme against keyword guessing attacks［J］.IEICE E-lectron Express，2009，6（5）：237-243

［8］Zhang R，Imai H.Generic combination of public key encryption with keyword search and public key encryption［A］.Proc.of Cryptology and Network Security，6th International Conference，CANS 2007，LNCS 4856［G］.Heidelberg：Springer-Verlag，2007：159-174

Revocable Public-Key Cryptosystems Formal Analysis

Yu Ruiqin
（Election Information Department，Zhenjiang College，Zhenjiang 212003，China）

Any setting，Public-key Infrastructure or Identity-Based.Must provide a means to revoke users from the system.Efficient revocation is a well-studied problem in the traditional Public-Key Infrastructure or Identity-Based Encryption.We propose revocable public key encryption with keyword search scheme of formalized definition and the security model in the paper.Based on bilinear dilinear diffie-hellman，the security of the scheme can be proved.

public key encryption with keyword search；revocation；bilinear pairings；secure channel free

王映苗】

1672-2027（2011）03-0075-03

TP309

A

2011-03-23

于瑞琴（1976-），女，山西孝义人，硕士，镇江高等专科学校讲师，主要从事网络与信息安全，计算机应用研究.