形式三角代数的零积导子

2011-01-07谢乐平

怀化学院学报 2011年5期

谢乐平

(怀化学院数学系,湖南怀化 418008)

假定A,B是两个有单位元的环,一个(A,B)-双模M是指M是一个左A-模,同时也是一个右B-模,并且 ∀a∈A,m∈M,b∈B,有(am)b=a(mb).形式三角代数定义为

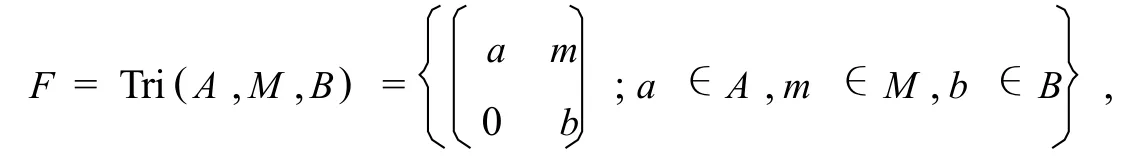
假定A,B是两个有单位元的环(不要求是交换环),M为有单位元的(A,B)-双模,1A,1B分别表示A,B的单位元,1为M的单位元.设F=Tri(A,M,B)为形式三角代数.我们称φ为F上的零积导子,是指 ∀x,y∈F,如果xy=0,那么一定有φ(x)y+xφ(y)=0.如果零积导子的运算是Lie运算[x,y]=xy-yx,则对应的零积导子我们称为Lie零积导子.

定理1导子一定是零积导子.

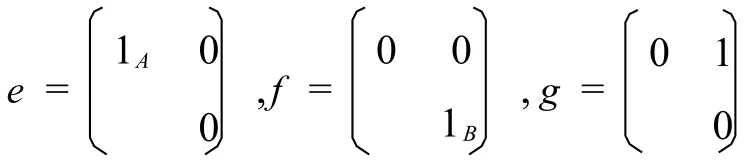
下面是本文的主要定理,给出了形式三角代数的零积导子的结构.

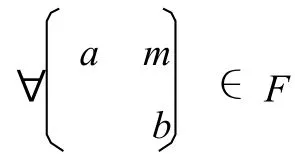
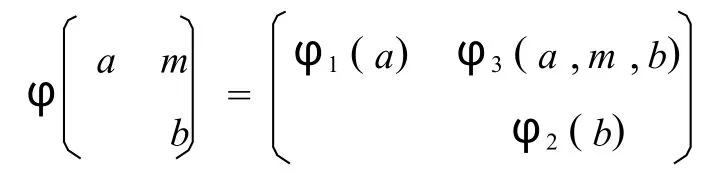
其中可加线性映射φ3满足φ3(1A,0,0)=-φ3(0,0,1B).

将所制备的混凝土试样1～5号养护28 d后进行收缩性检测.基准混凝土试样28 d收缩率为2.65×10-6，以低碳混凝土28 d的收缩率与基准混凝土收缩率的比值为收缩率比，测试结果如图2所示.由图2可知，低碳混凝土试样的收缩率比均小于基准低碳混凝土的收缩率比.当煅烧高岭土替代矿粉质量分数为20%时，试样的收缩率比为95%.继续增大煅烧高岭土的替代率，混凝土的收缩率比变化不明显.煅烧高岭土中含有大量的活化矿粉组分Al2O3 和SiO2，Al2O3和SiO2与Ca(OH)2反应生成硅铝酸盐结构的胶凝材料，进一步填充了混凝土的毛细孔，在一定程度上降低了其表面张力，减小了收缩率比.

证明e,f,g构成形式三角代数的一组基.

由ef=0,φ为零积导子,所以φ(e)f+eφ(f)=0,结合(1)式得

经过计算得

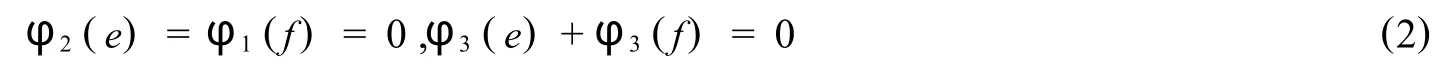
由ge=0,φ为零积导子,所以φ(g)e+gφ(e)=0,结合(1)式类似可得

由fg=0,φ为零积导子,所以φ(f)g+fφ(g)=0,结合(1)式类似可得

φ1(a,m,b)=φ1(a),φ2(a,m,b)=φ2(b).

再由 (2)式第二个等式可得φ3(1A,0,0)=-φ3(0,0,1B).定理2证毕.

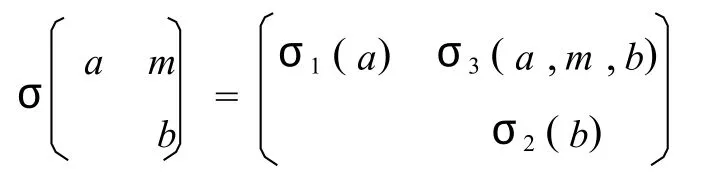
其中双模同态σ3满足σ3(1A,0,0)=-σ3(0,0,1B).

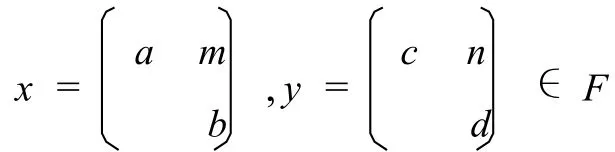
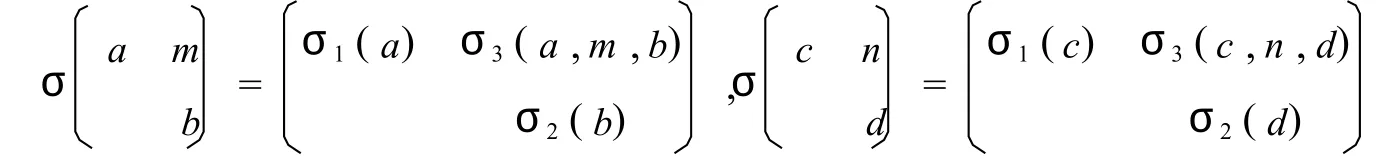
因为σ为导子,所以σ(xy)=σ(x)y+xσ(y).所以有

σ1(ac)=σ1(a)c+aσ1(c),σ2(bd)=σ2(b)d+bσ2(d)

即σ1,σ2为A,B上的导子.同时还有

σ3(ac,an+md,bd)=σ1(a)n+σ3(a,m,b)d+aσ3(c,n,d)+mσ2(d)

所以σ3为双模同态,同时由定理2还可得σ3满足σ3(1A,0,0)=-σ3(0,0,1B).

定理3形式三角代数F=Tri(A,M,B)上的零积导子一定是Lie零积导子.

证明设τ为形式三角代数F上的Lie零积导子,则 ∀x,y∈F,满足[x,y]=0,则有[τ(x),y]+[x,τ(y)]=0,等价于

[τ(x)y+xτ(y)]-[yτ(x)+τ(y)x]=0

如果τ为零积导子,则τ(x)y+xτ(y)=0.

又由[x,y]=0可得[y,x]=0,所以同样有yτ(x)+τ(y)x=0.

因此,形式三角代数F上的零积导子τ一定是Lie零积导子.

但是,零积导子不一定是导子.Lie零积导子也不一定是零积导子,下面列举一些简单的例子.

例1形式三角代数F=Tri(A,M,B),取A=B=Z(整数环),M为有理数域,∀x∈F,定义F上的线性映射μ(x)=kx(k∈Z).

当k=0,1时,μ显然是F上的零积导子.同时μ还是F上的导子.

当k≠0,1时,μ是F上的零积导子,但μ不是F上的导子.

例2形式三角代数F=Tri(A,M,B),设A=B,∀x=(a,m,b)∈F,定义F上的线性映射v(x)=(ψ(a),0,ψ(b)),其中ψ为A,B上非零的可加线性映射.

v为F上的零积导子,也是F上的Lie零积导子,但不是F上的导子.

例3形式三角代数F=Tri(A,M,B),∀x=(a,m,b)∈F,定义F上的线性映射ω(x)=(a+b,m+a-b,b+a).

ω为F上的Lie零积导子,但不是F上的零积导子.

[1]A.haghany,K.Varajan.Study offormal triangular matrix rings[J].Comm.Algebra,1999,27(11)：5507-5525.

[2]W.S.Cheung.Commuting maps of triangular algebras[J].J.London Math.Soc,2001,63(2)：117-127.

[3]W.S.Cheung.Lie derivations of triangular of triangular algebras[J].Linear Mult Algebra,2003,51：299-310.

[4]D.Benkovic,D.Eremita.Commuting traces and commutativety preserving maps on triangular algebras[J].J Algebra,2004,280：797-824.

[5]T.L.Wong.Jordan isomorphisms of triangular rings[J].Proc.Amer.Math.Soc,2005,133：3381-3388.

[6]J.H.Zhang,W.Y-yua.Jordan derivations of triangular algebras[J].Linear Algebra Appl,2006,419：251-255.

[7]谢乐平,曹佑安.形式三角矩阵环的导子和自同构 [J].数学杂志,2006,26(2)：165-170.

[8]Marin Gutana,Andrzej Kisielewicz.Rings and semigroups with permutable zero products[J].Journal of Pure and Applied Algebra,2006,206：355-369.

[9]Jian-Hua Zhang,An-Li Yang,Fang-Fang Pan.Linear maps preserving zero products on nest subalgebras of von Neumann algebras[J].Linear Algebra Appl,2006,412：348-361.

[10]Mikhail A Chebotar,Wen-Fong Ke.On Maps preserving zero Jordan products[J].Monatsh,Math,2006,149：91-101.

[11]Jinchuan Hou,Meiyan Jiao.Additive maps preservingJordan zero-products on nest algebras[J].Linear Algebra Appl,2008,429：190-208.