足球比赛中区域多人防守站位数学模型分析

陈 粮

(广东技术师范学院体育部,广东广州 510655)

足球比赛中,进攻与防守永远是对立统一的矛盾体,忽视任何一方,另一方都不可能获得真正的发展.积极地防守孕育着进攻,而区域多人协防是积极防守的重要形式之一.区域多人集体防守与个人防守的最大区别在于,个人防守区域 (能力)是相对固定的,而集体防守则会根据参与防守队员的能力、位置和运动状态的不同而改变防守区域而获得最佳防守效果.尽管足球比赛是流动的,但是否存在多人区域协防的最佳站位的固定模式,从已有的足球防守战术研究进展来看未见报道,考虑到足球比赛是在长方形场地上进行,因此,本研究运用数学建模与分析的方式,探讨足球区域防守中的多人协防的最佳站位模式 (或模型).

1 研究方法

数学建模与泛函数分析法[1].

2 结果与分析

2.1 操作原理

数学模型就是为了某种目的,用字母、数学及其它数学符号建立起来的用于描述客观事物的特征及其内在联系的数学结构表达式[1].为了定量地分析足球运动的防守战术问题特征,首先要对防守技术建立数学模型.

2.2 区域多人防守的数学模型构建

数学模型是关于部分现实世界和为一种特殊目的而作的一个抽象的、简化的结构.具体来说,如果将足球比赛中个人防守区域映射到平面上,就成为了一个近似的椭圆[2].在不考虑守门员的情况下,多人防守的数学意义是防守空间的连续性.这样把个人防守的“椭圆”组成了多人防守的“区域” (图1).本研究的目的在于,通过泛函数分析,求得多人防守空间映射到球场平面图上的、各防守球员之间形成的防线的合适距离.

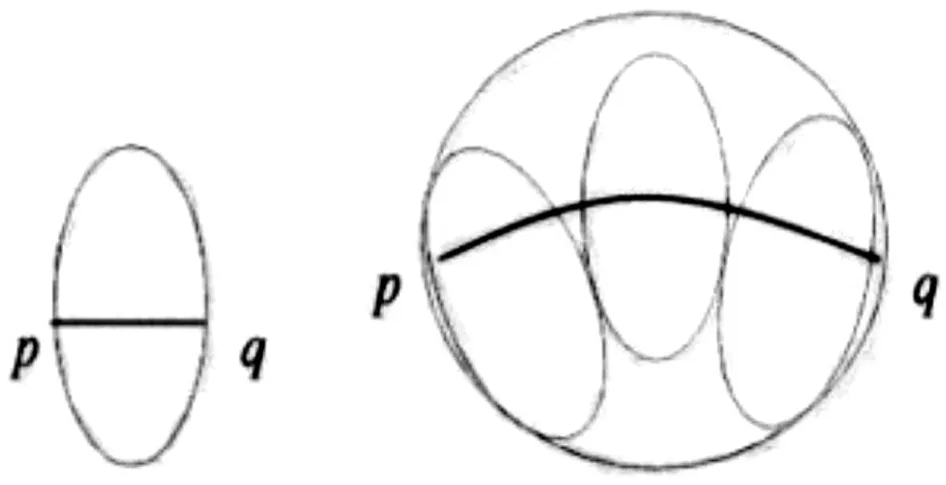
图1 区域多人防守的站位

多人防守在保证防守空间的连续性的前提下,形成了两个点分别设为p和q.

式中Lpq表示集体防守空间的防线,li表示参与防守的队员防守“椭圆”横轴的长度,n表示参与防守队员的数里.这样我们就通过定义1建立了多人防守的数学模型.

2.3 防守模型的泛函数分析

在定义1中,在Lpq一定的情况下,防守队员的站位可看成是形成防守空间最大的最优问题.为了简化问题,我们把防线看作是在oxy平面上的最优问题.

已知dl=dx2+dy2

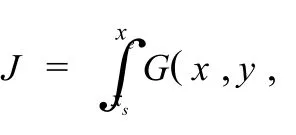
在所有曲线y中,可以确定一条曲线,

作辅助函数：H=F+λG

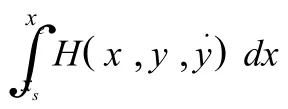
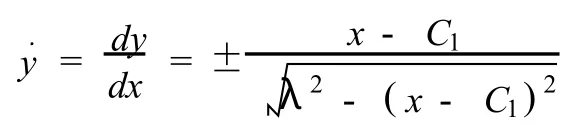
因此有：(x-C1)2+(y-C2)2=λ2,式中C1,C2和λ由等周条件和边界条件来确定.由此可见,多人防守的最佳防守方式是切割一弧线的连续直线.直线指的就是每个防守队员的防守“椭圆”横轴的长度.

3 结论

(1)足球区域防守临近队员的最佳站位模式是多人在满足个人成椭圆防守区域选择的条件下的多个椭圆防守区域的叠加(图1),此站位模式近似于足球区域防守前一后二的三角站位模式.

(2)多人防守的个人选位是沿一段弧线进行的.每个防守队员之间可以用一条虚拟的连接线来衔接,该虚拟连接线是一条连续切制的弧线,弧顶面对进攻方.弧线的长度符合公式： (x-C1)2+(y-C2)2=λ2(C1,C2和λ由等周条件和边界条件来确定).

[1]姜启源.数学模 [M].北京：高等教育出版社,1999.

[2]范毅方,罗家福,袁支润.基于力学的足球一对一防守技术分析 [J].西南民族学院学报,2002,28(2)：266-270.

[3]袁亚湘,孙文瑜.最优化理论与方法 [M].北京：科学出版社,1999.

[4]陈宝林.最优化理论与算法 [M].北京：清华大学出版社,1998.