青藏高原区MS-L回归关系式的不确定性分析1

李正芳 周本刚 王明明 陈 涛

（中国地震局地质研究所，北京 100029）

青藏高原区MS-L回归关系式的不确定性分析1

李正芳 周本刚 王明明 陈 涛

（中国地震局地质研究所，北京 100029）

本文收集了青藏高原区7级以上以走滑为主的30个地震的地表破裂参数资料，拟合出了青藏高原区新的震级与破裂带长度统计关系式，并结合前人的统计关系式，分别通过破裂带长度估算震级，求出了估算震级与仪器震级的差值。同时将差值为正值（即估算震级偏大）的归为一类，差值为负值（估算震级偏小）的归为另一类，做了分析和对比。研究发现，差值为正值的地震所处的走滑断裂带一般位于一级块体或次级块体的边界断裂带上；差值为负值的地震所处的走滑断裂带大多位于一级块体或次级块体内部断裂带或断裂带的交汇处。基于上述分类的差异，作者对不同回归关系计算的差值数据进行了统计分析，分别给出了修正计算结果不确定性的参考值，为降低估算震级的不确定性提供了理论依据。

青藏高原 震级 破裂带长度 不确定性分析

引言

活动断裂定量研究的资料在评价特定断裂上的强震危险性方面可发挥较大的作用，但由于受种种条件的制约，并不是每一条活动断裂上都可轻易获取所需的定量数据，并且这些数据本身通常含有较大的不确定性。活动断层长度作为活动断层定量数据之一，相比其他的数据较容易获得，不确定性较小，因而，断层破裂长度与震级的统计关系被广泛地应用于地震危险性分析和工程安全性评估。青藏高原区是一个地震频发的高危险区，也是地震防御的重点地区，为了最大限度地减少上述这种统计关系在该区的不确定性，较准确地预测未来地震的危险性，作者通过收集青藏高原区的走滑地震资料，拟合出了该区新的震级与破裂带长度的统计关系，并结合前人的统计关系式，对比和分析了估算震级与仪器震级的差值，达到了研究该区震级与破裂带长度统计关系式不确定性的目的。

1 研究概况

青藏高原构造区由几个不同时代、不同结构的亚板块拼合而成，同时在印度板块对欧亚板块的碰撞和推挤下，形成了一系列巨大的弧形活动走滑断裂带，构成了若干个“亚板块”的边界，是世界上地震发生最强烈的地区，也是研究地震发生最典型的地区之一。本文在系统地收集了青藏高原区内30个7级以上的走滑地震地表破裂资料（表1）的基础上，分析和研究了该区震级与破裂带长度统计关系的不确定性以及其主要的影响因素，为未来该区震级上限的确定提供了依据。

表1 青藏高原构造区以走滑为主的地震地表破裂参数统计（MS≥7级）Table 1 Statistics of strike-slip earthquake (MS≥7) surface rupture parameters in Tibetan Plateau

续表

图1 青藏高原震级（MS）与破裂长度（L）回归直线图Fig. 1 Regression curves of magnitude (MS) and rupture length (L) in Tibet Plateau

2 地震地表破裂带长度（L）与震级（MS）回归关系式

邓起东等（1992）利用青藏高原区23个典型的走滑地震实例得到了震级与破裂带长度的一元回归关系式：MS=5.92+0.88LgL，其剩余标准差为0.370。美国学者Wells等（1994）基于大量的样品数，建立了走滑地震地表破裂长度与矩震级的经验关系式（简称WC经验关系）：MW=5.16+1.12LgL，其剩余标准差为0.28。而在应用WC经验关系时，会遇到矩震级MW与面波震级MS之间的转换问题，Wells等（1994）认为当MS在5.7—8.0级之间时，两者之间不存在系统的差异，即MW≈MS。但由于我国所采用的震级测定方法和所用的台站资料与美国存在一定的差异，即我国大陆的MS与MW并不相同。鉴于此，冉洪流（2009）根据中国大陆1973—2008年的地震数据，得出了上述两种震级的转换关系式：MS=1.412+0.845MW，其剩余标准差为0.11。由此可换算出面波震级（MS）与破裂带长度（L）的关系式为：MS=1.412+0.845×（5.16+1.12LgL）。本文在前人工作的基础上，补充了青藏高原区新的地震资料（表1），利用一元线性回归方法重新拟合了该区震级与破裂带长度的统计关系式为：MS=0.81LgL+6.05，其剩余标准差为0.22。同时与前人的统计关系式进行了对比分析（见图1），发现基于30个地震资料的样品数据，本文拟合的效果更好，标准差更小。

本文分别采用上述3个统计关系式通过破裂带长度估算了震级MS1、MS2、MS3，并求出了估算震级与仪器震级MS的差值△MS1、△MS2和△MS3：

△MS1= MS1– MS， 其中MS1=5.92+0.88LgL（邓起东等，1992）

△MS2= MS2– MS， 其中MS2=1.412+0.845×（5.16+1.12LgL）（Wells等，1994；冉洪流，2009）

△MS3= MS3– MS， 其中MS3=0.86LgL+6.03（本文拟合）

通过对差值（表2）的对比和分析，可达到减少统计关系式不确定性的目的。

表2 估算震级与仪器震级差值一览表Table 2 Errors between estimated magnitudes and recorded magnitude

续表

3 基于MS-L回归关系式估算震级的不确定性分析

通过估算震级与仪器震级的差值（表2），结果显示用上述3种回归关系式估算的震级偏大、偏小的趋势基本保持一致。本文将差值大于零的归为一类（表3），差值小于零的归为另一类（表4），进而进行分析和对比，并在图2中将差值大于零的地震编号变为红色，差值小于零的地震编号变为黑色，旨在研究影响地震破裂带长度估算震级结果的因素。

3.1 差值△MS1、△MS2、△MS3＞0的分析和对比

利用青藏高原构造区的地震资料，计算的差值大于零，意味着采用断层长度回归关系式估算的震级偏大，如将估算的震级应用于未来某段震级的评估，就表现出保守，可能会使得工程造价较大。从归纳的表3和图2的显示中，可发现估算震级偏大的地震主要位于一级块体或次级块体的边界走滑断裂带上：1937年的花石峡地震（标号18）；2001年的昆仑山地震（标号28）（发生于柴达木地块与巴彦喀拉地块的边界断裂带—东昆仑活动断裂带上）；1997年的玛尼地震（标号27）（发生在东昆仑断裂带以西的玛尔盖茶卡断裂上）；2008年的汶川地震（标号29）（发生在巴彦喀拉地块与华南块体的边界断裂带—龙门山断裂带上）；1896年的邓柯地震（标号14）；2010年的玉树地震（标号30）（发生在巴彦喀拉地块与羌塘地块的边界断裂带—甘孜-玉树断裂带上）；1725年色拉哈段的地震（标号6）；1923年的道孚-炉霍地震（标号16）；1973年的炉霍地震（标号26）（发生在川滇地块的边界断裂带鲜水河断裂带上）；1733年的东川地震（标号7）；1850年的西昌地震（标号17）（发生在川滇地块与华南块体的边界断裂带—则木河断裂和小江断裂带上）；1609年的酒泉地震（标号4）（发生在祁连山山前断裂上）；1895年的塔什库尔干地震（标号13）（发生在青藏地块与塔里木盆地的边界断裂—塔什库尔干断裂上）。

从上述分析可发现，当估算震级与仪器震级之间的差值为正值时，与其相对应的地震所在的断裂带大多数都位于块体的边界断裂带上。

表3 差值为正值一览表Table 3 A list of faults with positive errors

续表

图2 青藏高原区强震（MS≥7）地表破裂分布简图（据邓起东，1992修改）Fig. 2 Distribution of surface ruptures by strong earthquakes (MS≥7) in Tibetan Plateau(after Deng Qidong, 1992)

3.2 差值△MS1、△MS2、△MS3＞0不确定性分析

根据表3中的数据，利用数学统计的方法作者绘制出了差值△MS1、△MS2、△MS3＞0的差值-频度排列图（图 3），排列图又称柏拉图或主次因素图，用双直角坐标系表示，左边纵坐标表示频数，右边纵坐标表示频率，图中的分析线表示累积频率。横坐标表示影响结果的各项因素，按影响程度的大小（即出现频数的多少）从左向右排列，通过对排列图的观察分析可以确定影响结果的主要因素。将影响结果好坏的因素分为三大类：累积频率在 0—60%区间的因素称为A类因素，它们的数量不多，但是影响结果好坏的关键因素；累积频率在60%—80%区间的因素称为B类因素，数量可能比A类的要多，但对结果的影响比A类小；累积频率在80%—100%区间的因素称为C类因素，数量较多，但对结果的影响特别小。本文主要考虑影响统计结果误差的主要因素，对比图4中的累积频率曲线图可发现，△MS1累积频率为0—60%，影响该统计关系结果的主要因素值分别为0.02、0.14、0.36、0.06、0.08和0.12，其平均值约为0.13；△MS2累积频率为0—60%，影响该统计关系结果的主要因素值分别为0.02、0.14、0.52、0.08和0.12，其平均值约为0.18；△MS3累积频率为0—60%，影响该统计关系结果的主要因素值分别为0.06、0.08、0.14、0.36和0.04，其平均值约为0.14。因此，可以选用0.13、0.18和0.14，作为修正△MS1、△MS2和△MS3＞0相对应统计关系计算结果的参考值。

通过上述分析可知，当利用地震破裂长度估算震级时，如果破裂带位于块体边界断裂带上，利用上述3种震级经验关系式估算出的震级偏大，而针对不同的统计关系式作者还给出了相对应的修正值，如利用相应的震级与破裂长度的关系式估算震级，应该将计算出的震级减去相应的修正值，从而在一定程度上可减少估算震级的不确定性。

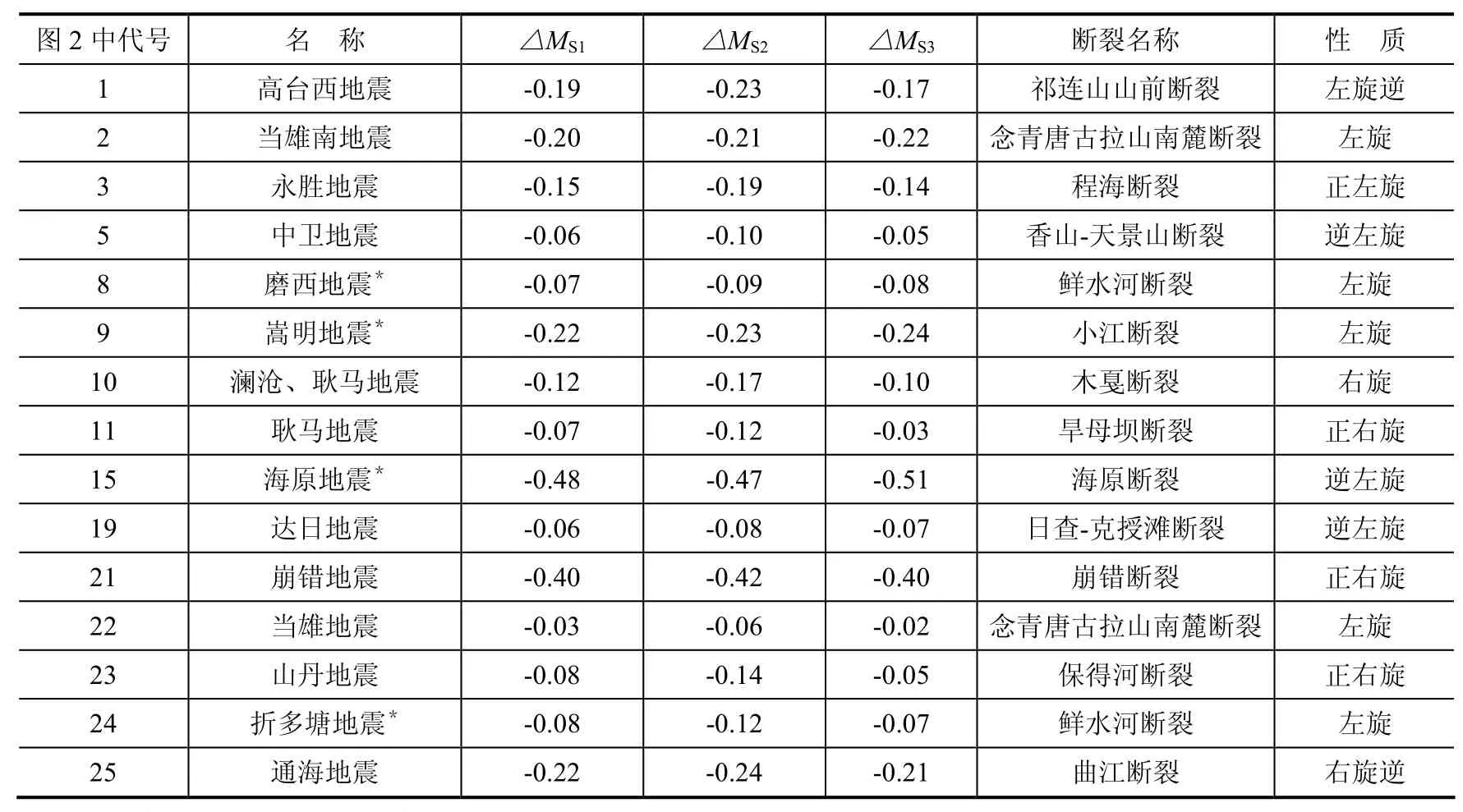
表4 差值为负值一览表Table 4 A list of faults with negative errors

3.3 差值△MS＜0的分析和对比

当计算的差值△MS＜0时，意味着采用震级与破裂带长度回归关系式估算的震级偏小，如将估算的震级应用于未来某段震级的评估，就表现出其不安全性。从归纳的表4和图2的示意中可发现，估算震级偏小的地震大多发生在地块内部的断裂带或断裂带的交汇处：1511年的永胜地震（标号3）（发生在程海断裂上）；1970年的通海地震（标号25）（发生在曲江断裂带上）。这2条断裂带都属于川滇地块的内部断裂带。1709年的中卫地震（标号为5）（发生在香山-天景山断裂带上）；1954年的山丹地震（标号23）（发生在保得河断裂带上）。这2条断裂带均位于柴达木地块的内部。1411年的当雄南地震（标号2）；1952年的当雄地震（标号22）（发生在念青唐古拉山南麓断裂带上）；1951年的崩错地震（标号21）（发生在崩错断裂带上）。这2条断裂带都属于青藏块体内部断裂。1947年的达日地震（标号19）（发生在巴彦喀拉地块内部的日查-克授滩断裂上）；1988年的云南澜沧、耿马地震（标号10、11）（分别发生在藏北地块内部的木噶断裂和旱母坝断裂带上）。

从上述分析可知，当估算震级与仪器震级的差值小于零时，绝大多数地震所在的断裂带都属于块体内部的断裂或断裂的交汇部位处。而需要特别指出的是，1920年发生在海原断裂带上的海原地震（标号15），该地震的震级达到8.6级，所得到的地表破裂带长度仅为246km，而据文献资料（国家地震局地质研究所，1990）推测，这是由于海原断裂带东麓存在六盘山逆冲带，吸收了部分能量所致，因此，破裂带长度估算出的震级也偏小，计算出的差值可作为特例处理。

图3 差值△MS1、△MS2和△MS3的排列图和累积频率分布图Fig. 3 Arrangement graph and cumulative frequency distribution diagram of errors △MS1，△MS2 and △MS3

3.4 差值△MS1、△MS2、△MS3＜0的不确定性分析

根据表4中差值小于零的数据，作者分别绘制了各个差值的排列图和累计频率图（图3），利用与3.2节同样的方法来寻找影响统计结果误差的主要因素。对比图4中3种差值小于零的累积频率曲线图可发现，△MS1累积频率为0—60%，影响该统计关系结果的主要因素值分别为0.06、0.22、0.48和0.4，其平均值约为0.29；△MS2累积频率为0—60%，影响该统计关系结果的主要因素值分别为0.22、0.12、0.08、0.46和0.24，其平均值约为0.22；△MS3累积频率为0—60%，影响该统计关系结果的主要因素值分别为0.06、0.04、0.02、0.5、0.4和0.24，其平均值约为0.21。同理，我们分别选用0.29、0.22和0.21，作为修正△MS1、△MS2和△MS3＜0时相对应统计关系计算结果的参考值。为此，当采用上述3种统计关系式，利用地表破裂长度估算震级时，若估算的震级偏小应根据本文给出的不同经验关系式的修正值，将估算的震级加上一个值，以确保估算震级的安全性。

4 结论和讨论

4.1 结论

本文利用青藏高原区30个震级大于7级的走滑地震资料，拟合出了青藏高原区新的震级与破裂带长度的统计关系式，并结合前人的统计关系式分别估算了震级，计算出与仪器震级之间的差值，同时通过对差值的进一步分析和对比，得到了如下结论：

（1）新拟合出的震级与破裂带长度统计关系式的资料相比前人的更丰富，估算的结果误差较前人的小，值得在青藏高原区采用断裂破裂长度估算震级时使用。

（2）采用3种统计关系式计算出的差值虽然在数值上存在少许差异，但整个差值反映出利用断层长度估算震级偏大和偏小的趋势是保持一致的。对估算震级偏大和偏小的地震作了归类，结合地震发生所处的断裂带的性质和地质构造环境，发现估算震级偏大的地震大多位于一级块体或次级块体的边界走滑断裂带上；估算震级偏小的地震大多位于块体内部的断裂带或活动断裂带的交汇处。

（3）通过对差值的归类和统计分析，分别为3种MS-L回归关系式赋予了修正参考值。当破裂带位于块体的边界走滑断裂带上，利用 MS-L回归关系式估算的震级偏大，应将估算的震级减去文中提供的修正值；当破裂带位于活动块体的内部断裂带或断裂带的交汇处，利用MS-L回归关系式估算的震级偏小，应将估算的震级加上文中提供的修正值。

4.2 讨论

文中采用3种震级破裂带长度估算震级的统计方法，计算了估算震级与仪器震级的误差，发现误差偏大和偏小存在一定的规律性，在上述的表和图中均有显示，虽存在个别的特例，但整体反映的这种规律性以及与构造环境的对应性，在前人的研究中是未提及的。同时对计算的误差数据做了统计分析，利用排列图和累计频率的方法分别给出了3种统计关系修正误差的参考值，虽然数据统计拟合的效果还不太理想，缺乏较高的准确性，但仍可在一定程度上减少利用MS-L回归关系式估算震级的不确定性。

总之，利用地震地表破裂带长度估算震级的影响因素很多，本文仅对断裂带的性质和所处的地质构造环境影响进行了讨论，意在提出该方面的认识以供进一步研究。虽在一定程度上忽略了地表介质、震源深度、破裂带的走滑速率等因素对震级的影响，但在今后的研究工作中对这些影响因素还可以进行进一步的补充和修正，以求降低估算震级的不确定性。

邓起东，于贵华，叶文华，1992．地震地表破裂参数与震级关系的研究．见：国家地震局地质研究所编，活动断裂研究（2）．北京：地震出版社：247—264．

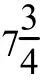
董治平，赵仪全，慕文斋等，2005. 1954年山丹7（1/4）级地震概述. 西北地震学报，27（S1）：21—28.

冯先岳，李军，张勇，1988. 1985年乌恰7.4级地震形变带. 地震地质，10（2）：7—18.

国家地震局地质研究所，宁夏自治区地震局，1990. 海原活动断裂带. 北京：地震出版社.

国家地震局地质研究所，1993. 祁连山-河西走廊活动断裂系. 北京：地震出版社.

虢顺民，向宏发，张靖等， 1988. 1515年云南永胜地震形变带和震级讨论. 地震研究，11（2）：43—52.

龙德雄，邓天岗，1990. 1786年康定地震形变特征的初步研究. 地震研究，13（1）：53—62.

李陈侠，戴华光，陈永明等，2006. 对1937年托索湖7.5级地震若干问题的探讨. 地震地质，28（1）：12—21．

李天昭，杜其方，游泽李，1992. 折多塘断裂的新活动与1955年7.5级地震. 见：活动断裂研究（2）. 北京：地震出版社．

马寅生，张永双，胡道功等，2010. 玉树地震地表破裂与宏观震中. 地质力学学报，16（2）：116—128.

冉洪流，2009. 潜在震源区震级上限不确定性研究. 地震学报，31（3）：396—402.

唐荣昌，1976. 1973年炉霍7.9级地震的地裂缝特征及地震成因的初步探讨. 地球物理学报，19（1）：20—29.

汪一鹏，宋方敏，李志义等，1990. 宁夏香山-天景山断裂带晚第四纪强震重复间隔的研究. 中国地震，6（2）：15—24.

汪一鹏，俞维贤，宋方敏等，1996. 1833年云南嵩明8级大地震地表破裂带的考查研究. 地震研究，19（4）：385—390.

吴章明，曹忠权，邓起东，1990. 1411年西藏当雄南8级地震地表破裂. 地震地质，12（4）：98—108.

吴章明，邓起东，1989. 西藏崩错8级地震地表破裂的变形特征及其破裂机制. 地震地质，11（1）：17—27.

徐锡伟，1999. 藏北玛尼地震科学考察. 见：刘玉辰主编，中国地震年鉴. 北京：地震出版社：327—329.

徐锡伟，陈文彬，于贵华等，2002. 2001年11月14日昆仑山库赛湖地震（MS8.1）地表破裂带基本特征．地震地质，24（1）：1—13.

徐锡伟，闻学泽，叶建青等，2008. 汶川MS8.0地震地标破裂带及其发震构造. 地震地质，30（3）：597—629.

徐锡伟，闻学泽，于贵华等，2005. 川西理塘断裂带平均活动速率、地震破裂分段与复发特征. 中国科学（D辑），35（6）：540—551.

俞维贤，柴天俊，侯学英，1991. 澜沧7.6级地震形变带. 地震地质，13（4）：57—66.

俞维贤，宋方敏，闻学泽等，2001. 1850年西昌地震地表破裂带的考察研究. 地震研究，24（4）：69—73.

张俊昌，1988. 1970年通海地震断层的特征. 见：中国地震断层研究. 乌鲁木齐：新疆人民出版社.

周瑞琦，俞维贤，谷一山等，1990. 云南耿马7.2级地震地表破裂带研究. 地震地质，12（4）：3—14.

周荣军，马声浩，蔡长星等，1996. 甘孜-玉树断裂带的晚第四纪活动特征. 中国地震，12（3）：250—260.

朱成男，滕德贞，段加乐等，1988. 1733年东川地震的地表破裂. 见：中国地震断层研究. 乌鲁木齐：新疆人民出版社.

Wells D.L., Coppersmith K.J., 1994．Updated empirical relationships among magnitude, rupture length, rupture area,and surface displacement．Bull. Seism. Soc. Am., 947—1002．

The Uncertainty Analysis of MS-L Regression Relation in the Qinghai-Tibet Plateau Region

Li Zhengfang, Zhou Bengang, Wang Mingming and Chen Tao
(Institute of Geology, China Earthquake Administration, Beijing 100029, China)

We collected 30 strike-slip dominant surface rupture parameters of the earthquake with MS≥7.0 in the Qinghai-Tibet Plateau region, and gave out the new statistical relationship of magnitude and rupture length. By using our relationship combined with the previous study, we calculated the error between the estimated magnitude and the magnitude that was measured by the instrument. The errors then are classified into two categories in terms of positive quantity and negative quantity. Through analysis and comparison, we found that the strike-slip fault along which earthquake occurred is typically located in a block or sub-block boundary fault when the errors are in positive quantity, whereas the strike-slip fault along which earthquake occurred is typically located in fault within the block and sub-block or the interchange of the fault when the error is negative. Our results are valuable to reduce the uncertainty of estimated magnitude in the future.

李正芳，周本刚，王明明，陈涛，2011. 青藏高原区MS-L回归关系式的不确定性分析. 震灾防御技术，6（3）：209—219.

地震行业科技专项“走滑活断层定量数据评定潜在震源区参数研究（200808018）”资助

2011-04-20

李正芳，女，生于1981年。中国地震局地质研究所在读博士研究生。主要研究方向：工程地震和地震危险性评价。E-mail：lizhengfang07@163.com

Κey words: The Qinghai-Tibet Plateau；Magnitude；The length of surface rupture； Uncertainty analysis