双单子对与缠绕结构
2011-01-05代瑞香王顶国
代瑞香,王顶国
双单子对与缠绕结构
代瑞香1,王顶国2
(1石河子大学师范学院数学系,石河子,832003;2曲阜师范大学数学科学学院,曲阜,273165)
根据余单子对、双单子对及对角模的定义及性质,构造了两个新的余单子对角模,证明了可分配余单子与余单子对之间的等价关系,得出了双单子对具有缠绕结构的结论。
余单子对;双单子对;对角模
近20年来,随着量子群研究的兴起,以及Kaplansky某些猜想的解决,Hopf代数理论日臻完善,它的一些推广概念如单子、Hopf单子、缠绕结构等也越来越受到重视,尤其是缠绕结构的Frobenius性质和 Maschke定理[1]。
缠绕结构源于非交换几何,它在Hopf代数中的一个重要的作用是为Doi-Hopf模、Yet ter-Drinfeld模、Hopf模、分次模等提供了一个统一的结构框架,,即缠绕模、Brzezinski F 等[2]研究了缠绕结构及其表示范畴;Moerdij k[3]介绍了张量范畴上的Hopf单子,并研究了Hopf单子的代数结构等性质;代瑞香等[4]将代数和余代数的缠绕结构上的一些结论推广到单子和余单子的缠绕结构上,之后代瑞香等[5]根据余环上的余导子与余整合的定义及性质,给出了T-余单子上的余导子、余整合的定义,并在它们构成的阿贝尔群之间构造了一个同构关系;在余环的余可分性质基础上刻画了余单子余可分、忘却函子可分与余积分存在之间的相互等价关系。
受计算科学中一些问题的启发,Hagino[6]引入了(F,G)-对角模的概念,其中F,G:A→B为任意两个范畴A、B之间的函子。对角模可以看作是对模和余模的总结和概括,Wisbauer R[7]用抽象的范畴理论给出了对角模的一些讨论,有关对角模在代数上的应用还有待进一步研究。关于代数和余代数在广义代数和计算科学中的更深层次的应用,可参考文献[8]。
本文在上述研究的基础上构造两个新的对角模,给出可分配余单子与余单子对的相互构造,刻画双单子对与缠绕结构的相互关系,从而拓展并丰富Hopf代数及单子的理论知识。
1 预备知识
定义1[9](G,Δ,ε)称为范畴C上的余单子,若函子G∶C→C及自然变换Δ∶G→GG和ε∶G→idC,满足GΔ·Δ=ΔG·Δ;εG·Δ=Gε·Δ=idG。
定义2[7]给定范畴C 的两个余单子(G,δ,ε)和(T,δ′,ε′),自然变换φ:TG→GT若满足Gφ·φG·Tδ=δT·φ;εT·φ=Tε·Gδ′·φ=φT·Tφ·δ′G;Gε′·φ=ε′G,则称φ为余单子可分配的。
定义3[7]若(G,δ,ε),(T,δ′,ε′)为范畴C 的两个余单子,自然变换φ:TG→GT是余单子可分配的,A∈obj(C)称为(G,T)-双余模,若A 为G-余模,其中α∶A→GA,且A为T-余模,其中β∶A→TA,并且满足相容条件Gβ·α=φA·Tα·β。
定义4[7]给定范畴C的两个自同态函子F,G∶C→C称(F,G)为范畴C的余单子对,若存在自然变换k∶FG→GG,f∶G→F,φ=Gf·k∶FG→GG→GF满足k G·Fk=Gk·φG·Fk;f G·k=idFG。
定义5[7]若(F,G)为余单子对,称A∈obj(C)为(F,G)-对角模,若态射γA∶F(A)→G(A)满足kA·FγA=GγA·φA·FγA;fA·γA=idF(A)。
若A,A′为(F,G)-对角模,态射f∶A→A′成为(F,G)-对角模态射,若G(f)·γA=γA·F(f)。
注:1)若函子F∶C→C,(F,I)-对角模就是F-模,(I,F)-对角模就是F-余模。
2)F,G∶C→C为自同态函子,若存在自然变换α∶F→G,则任意的A∈obj(C)都是(F,G)-对角模,其中αA∶F(A)→G(A)。
定义6[10]设C为 Monoidal范畴,(T,μ,η)和(G,Δ,ε)分别为C上的单子和余单子,ψ∶TG→GT为(T,μ,η)和(G,Δ,ε)的混合分配律,即满足ψ·μG=Gμ·ψT·Tψ;ψ·ηG=Gη;ΔT·ψ=Gψ·ψG·TΔ;εT·ψ=Tε,则称(T,G,ψ)为C上的缠绕结构。
定义7[7]给定范畴C的两个自同态函子F,G∶C→C,称(F,G)为范畴C的双单子对,若存在自然变换υ∶FG→GG,θ∶G→F,ψ=Gθ·υ∶FG→GG→GF满足θG·υ=idFG;υG·Fυ=Gυ·ψG·Fυ。
2 主要结论
定理1: 设(F,G)为范畴C的自同态函子的余单子对,则
1)任意的A∈obj(C),则G(A)为(F,g)-对角模,其中γG(A)=kA∶FG(A)→GG(A)。
2)若A∈obj(C)为(F,G)-对角模,其中γA∶F(A)→G(A),则F(A)为(F,G)-对角模,其中γF(A)=φA·F(γA)∶FF(A)→FG(A)→GF(A)。
证明:由(F,G)为范畴C的自同态函子的余单子对,则存在自然变换k∶FG→GG,f∶G→F,φ=Gf·k∶FG→GG→GF满足k G·Fk=Gk·Fk,f G·k=idFG。
1)因为
GγG(A)·φGA·FγG(A)=GKA·φGA·FkA=kA·FkA=γG(A)·FγG(A),
kA·fGA=γG(A)·fGA=idF(GA)。即G(A)为(F,G)-对角模。
2)因为
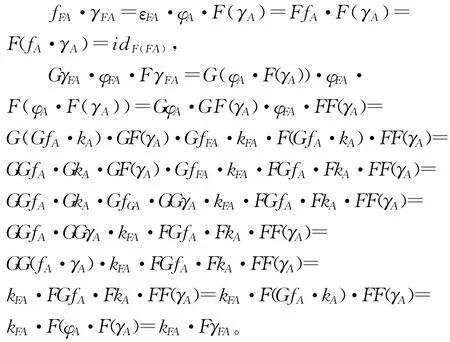
即F(A)为(F,G)-对角模。
定理2:给定范畴C的两个余单子(G,δ,ε),(F,δ′,ε′)自然变换φ∶FG→GF为余单子可分配的当且仅当(G,F)为范畴C的余单子对。
证明:若自然变换φ∶FG→GF为余单子可分配的,则满足
Gφ·φG·Fδ=δF·φ;
εF·φ=Fε,Gδ′·φ=φF·Fφ·δ′G;
Gε′·φ=ε′G。
定义k=δ·Gε′·φ∶FG→GF→G→GG,f∶G→F为任意的余单子态射,则
Gf·k=Gf·δ·Gε′·φ=φ;
且kG·Fk=(δ·Gε′·φ)G·F(δ·Gε′·φ)=

即证(G,F,k,f)为范畴C的余单子对。
反之,若(G,F,k,f)为范畴C 的余单子对,根据定义4,有
εF·φ=εF·Gf·k=Fε·f G·k=Fε;Gε′·φ=Gε′·Gf·k=ε′G·f G·k=ε′G;
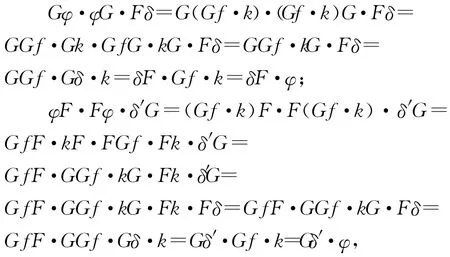
即自然变换ψ∶FG→GF为余单子可分配的。
定理3: 设(T,μ,η),(G,Δ,ε)分别为C 上的单子和余单子,若(T,G,υ,θ,ψ)为范畴C 的双单子对,则(T,G,ψ)具有缠绕结构ψ。
证明:由(T,G,υ,θ,ψ)为范畴C 的双单子对,根据定义7,有
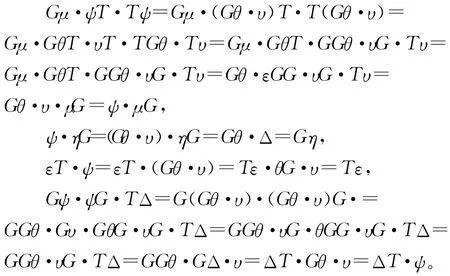
即(T,G,ψ)具有缠绕结构ψ。
[1]Brzezinski T.Frobenius properties and Maschke-type theorems for ent wined modules[J].Proc Amer Math Soc,1999(128):2261-2270.
[2]Brzezinski T,Caenepeel S,Militaru G,et al.Frobenius and Maschke-type Theorems f or Doi H-opf modules and ent wined modules revisited:a unified approach[M].New Yor k:Marcel Dekker,2001:1-32.
[3]Moerdijk I.Monads on tensor categories[J].J Pure Appl Algebra,2002,168:189-208.
[4]代瑞香,刘超,王顶国.缠绕结构与缠绕模[J].石河子大学学报:自然科学版,2008,26(1):106-109.
[5]代瑞香,刘超.余导子与余积分及其性质[J].石河子大学学报:自然科学版,2010,28(5):658-660.
[6]Hagino T.A categorical programming language[D].Edinbur gh:University of Edinburgh,1987:55-60.
[7]Wisbauer R.Algebras Versus Coalgebras[J].Applied Categorical Str uctures,2008,16,(1):255-295.
[8]Gumm H P.Universelle Coalgebra[M]∥Ihringer,Th.Allgemeine Algebra.Berlin:Helder mann,2003:155–207.
[9]Bruguieres A,Virelizier A.Hopf Monad[J].Adv Math,2007,215(2):679-733.
Bi monadic Pairs and Ent wining Structures
DAI Ruixiang,Wang Dingguo
(Depart ment of Mathematics,Teachers College,Shihezi University,Shihezi,832003 Depart ment of Mathematics,Qu Fu Nor mal University,Qu Fu,273165)
Accor ding to the definitions and pr operties of co monadic pairs,bi monadic pairs and ent wining str uctures,t wo new comonadic di modules were given firstly,then equivalent relations bet ween distributive co monads and co monadic pairs was constr ucted,finally the pr oof of bi monadic pairs have the ent wining str ucture was given.
co monadic pair;bi monadic pairs;di modules
O154.1
A
1007-7383(2011)04-0526-03
2010-01-07
国家自然科学基金项目(10671016),石河子大学高层次人才科研启动资金项目(RCZX200735)作者简介:代瑞香(1980-),女,讲师,从事环与代数、Hopf代数与量子群研究;e-mail:dair x129@163.com。
