基于网络Voronoi图启发式和群智能的最大覆盖空间优化
2011-01-04谢顺平冯学智都金康
谢顺平,冯学智,都金康
南京大学地理与海洋科学学院,江苏南京210093
基于网络Voronoi图启发式和群智能的最大覆盖空间优化
谢顺平,冯学智,都金康
南京大学地理与海洋科学学院,江苏南京210093
提出一种基于网络Voronoi面域图的最大覆盖选址模型及相应的粒子群优化方法,为城市化区域响应敏感型公共服务设施的空间优化提供技术方法。考虑设施功能沿交通网络传导以及需求非均匀连续分布情形,对设施在网络连续空间上进行布局优化,选址模型采用网络Voronoi面域图划分布局设施的功能辐射域,以启发空间优化最小化重叠覆盖。模型最大化设施利用效率,设施功能对覆盖半径以内的需求完全覆盖,对覆盖半径以外的需求部分覆盖。提出一种集成遗传机制和广义Voronoi图的改进粒子群算法,以提高连续网络空间内的空间优化性能。对南京市消防站最大覆盖选址优化的试验表明,该研究取得较为理想的结果。
网络Voronoi面域图;空间优化;最大覆盖选址模型;Voronoi图启发式;粒子群算法
1 引 言
空间优化作为GIS实现空间决策的一项关键技术,已成为相关领域研究热点,随着计算机科学、人工智能、地理空间分析技术的发展,使得有效解决城市化区域复杂的空间优化问题成为可能。Voronoi图空间分析模型在位置问题描述、模拟位置产生的空间结构、选址模型构建、图启发式等方面具有独特功能和应用潜力,一些学者研究了Voronoi图在空间优化分析中的理论和方法。文献[1]较早提出解决p-中心问题的Voronoi图启发式方法,即初始在区域内随机产生p个中心位置,构建相应的Voronoi图,将p个中心再移位到对应Voronoi多边形的1-中心解上,如果最大中心位移小于预设容限,则问题获解。否则,继续构建Voronoi图迭代。文献[2]就可通过Voronoi图启发式求解的一类连续位置优化问题进行了深入讨论,并给出用Voronoi图参与描述的连续p-中值问题选址模型和相称问题选址模型。文献[3]认为设施布局选址的纯解析计算可变换为图论与解析计算相结合问题,并将全局范围内的p-中值选址转化为基于Voronoi图的分区p-中值选址。文献[4—5]提出了一种启发式Voronoi图算法,以解决限制空间中离散需求点p-中心问题和覆盖问题。文献[6]发展了一种确定有限数目相同传感器位置的Voronoi图启发式方法,使用Voronoi图评估非检测概率并引导搜索方向。此外,Voronoi图还被应用于空间竞争分析模型[7]。
近年来,随着城市交通网络体系的完善,可达性和距离的时间效应改变了人们的择近视角。交通网络对城市公共服务设施服务范围的影响日趋明显,常规Voronoi图分析应用于城市化区域的局限性和缺陷逐渐显现。这种基于平面欧氏距离的空间分割方法由于未能体现城市空间传导和阻隔机制,因而不能准确表达城市化区域服务域的空间形态[8]。作为其适应道路网络环境的扩展模型,网络Voronoi面域图是一种基于网络路径代价(长度、时间、费用、效率等)距离度量的空间划分模型。它通过最短路径分析分别对网络空间中的结点和弧段进行邻近最近发生元的分割,进而采用面线邻近分析对平面空间进行划分而成,可模拟城市各类功能辐射与吸引的网络传导机制和服务覆盖格局,更适用于城市化区域的空间分析[8-12]。文献[8—9]在评估城市零售商业需求分布中用路径时间代替路径距离,并认为网络Voronoi图是划分城市化区域功能服务域较为精确的方法,国内学者也开始研究网络Voronoi面域图的构建算法及其在城市商业设施服务域分析中的应用[10-12]。随着网络Voronoi图模型及其构建算法的成熟,这一模型参与城市空间分析和空间优化将成为趋势。
空间优化问题的精度、规模和复杂性要求优化算法具有更高的启发式性能,以克服优化过程中的计算瓶颈。粒子群优化算法具有独特与简洁的仿生进化机制和突出的寻优能力,尤其对目标函数及其约束条件的连续性和凸性具有较强的抗差性[13-14],是极具空间优化应用潜力的群智能启发式方法[15-17]。由于空间优化基于空间位置分布评估的特点,需要模拟由位置产生的空间结构参与分析和启发。将网络Voronoi图启发式和智能启发式结合起来,充分发挥各自的优势和结合增强的优化性能,是解决城市化区域复杂空间优化问题的一条值得探索的途径。
2 最大覆盖选址模型
2.1 最大覆盖选址模型及其研究进展
现实中有一类设施的功能或提供的服务受时间和距离制约,如消防站、急救中心、救援中心等一些应急服务设施,这类设施提供的服务具有较强的时效性,它们必须在规定的时间内响应服务请求并实现服务。因此,这类设施必须布设在与潜在需求分布特定的距离以内,才有可能提供有效的服务,确定这类设施的优化位置属于覆盖问题范畴[18]。有集合覆盖与最大覆盖两类覆盖问题。集合覆盖问题模型的目标是用最少的设施配置用去覆盖所有需求。通常,满足覆盖全部需求的设施建设成本难以承受,并会导致设施利用率降低。如果在限定设施数目条件下,确定它们的位置使得覆盖尽可能多的需求量,这就是最大覆盖问题(maximal covering location problem,MCLP)。由于最大覆盖问题的实用意义较为突出,已成为相当一段时期该领域的研究热点[18-24]。
文献[19]针对现有研究需求点状分布与现实的不符,借助GIS用多边形空间目标表达需求分布,给出融合协同部分功能覆盖的最大覆盖模型。文献[20]研究了基于区域内分割面元的需求表达的覆盖建模方法,并成功应用于都柏林城市区域警报设施选址优化。文献[21—22]认为设施对覆盖半径以外的需求仍有逐步衰减的功能覆盖,并研究了可变半径覆盖、逐级覆盖、协同覆盖等的广义覆盖问题。文献[23]研究了通过适度完善道路网络系统改善医疗服务设施对刚果偏远地区最大覆盖的优化模型。文献[24]在基于时间满意的网络最大覆盖选址问题中,将覆盖半径的概念由从设施角度出发,转变为由离散需求点视角出发。可以看出,最新的最大覆盖空间优化研究已开始顾及需求的连续面状分布、交通网络影响和有限资源条件下的部分覆盖策略等,但待优化设施基本只能在网络结点集或预定的一组候选点集上布设,缺乏基于道路网络环境分析的最大覆盖实用模型和空间分割图形启发式与智能启发式结合的空间优化方法。
2.2 基于网络Voronoi图的最大覆盖模型
本文设计的最大覆盖模型考虑需求在区域内连续非均质分布,规定覆盖半径由设施站点角度出发,设施功能对覆盖半径以内的需求完全覆盖,对覆盖半径以外需求部分覆盖,部分覆盖强度随距离逐步衰减。在限定资源条件下,追求设施功能的非重叠覆盖是最大化覆盖效率的前提。由于网络Voronoi面域图是对功能覆盖的非重叠分割,优化算法最大化这种分割所达到的设施功能覆盖需求总和,必然会最小化重叠覆盖,所以基于网络Voronoi面域图的最大覆盖模型具有启发最小化重叠覆盖的性能。
网络上的最大覆盖问题可分为连续最大覆盖问题和离散最大覆盖问题,其差别在于设施可以在整个网络路段上布设,还是只能在网络节点上布设。网络连续最大覆盖问题是颇具挑战性的空间优化难题,但其实用意义却是显而易见的。根据最大覆盖问题的性质,设施覆盖域为以覆盖半径确定的网络辐射缓冲区,考虑部分覆盖时,还要顾及功能辐射呈逐步衰减的外延缓冲带。追求重复覆盖的最小化要求在最大覆盖模型中不考虑重复覆盖的需求统计,因此,网络Voronoi图是非常适合的功能覆盖提取模型。为此,本文提出的基于网络Voronoi图的连续最大覆盖问题的数学模型描述如下

式中
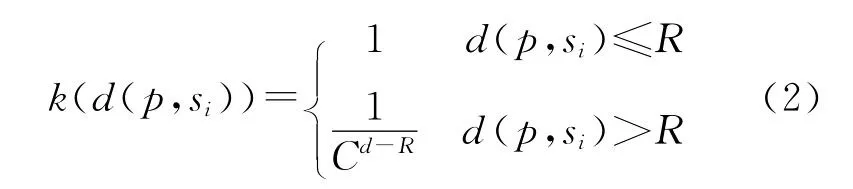
n为参与配置和优化的设施数,n个设施分别为s1,s2,…,sn,它们的位置由粒子群优化过程中产生的代表一种设施布局方案的一个粒子坐标提供;p为需求点;vi为设施si的网络Voronoi多边形覆盖区域,vi内分布的需求p到设施的距离由两部分组成,其中dE(p,pm)为vi内需求p点到最近道路的直线路径代价距离,dN(pm,si)为需求点p邻近道路上的最近点pm到网络上最近设施si的网络路径代价距离,当采用路径长度代价时,dE(p,pm)与等长度的道路路径代价相同,当采用路径时间代价时,dE(p,pm)与等长度最低等级道路路径时间代价相同;f为点p处的需求密度;dp为p点处的面积微元;k(d)为距离衰减函数;R为覆盖半径;C为大于1的常数,如果距离d从R到2R,k(d)从1.0衰减到0.1,则C取值为101/R,当然,k(d)亦可采用线性衰减方式。最大覆盖模型目标函数的计算可由集成到网络Voronoi面域图模型中的信息获取与分析计算功能实现[10],通过与预先空间栅格离散化的区域需求叠加处理,提取各个网络Voronoi多边形区域内的需求信息,并进行目标函数的计算。显然,上述模型追求布局设施通过道路网络去覆盖最大的区域需求总量。
3 粒子群空间优化
粒子群优化(PSO)是一种基于群体搜索的算法,它建立在模拟鸟群社会的基础之上。文献[14]对Heppner模型进行了修正,模拟由众多无质量和体积的粒子组成的群体在搜索空间中以一定的矢量速度飞行,每个粒子在搜索时,考虑自己曾搜索到的最好解和邻域或群体内其他粒子搜索到的历史最好解,并据此调整自身的飞行速度和位置,使粒子能够飞向解空间,并在最优解处积聚。自粒子群算法提出以来,引起相关领域学者的关注并成为优化应用研究热点,针对具体应用出现了各种改进方法[13-14]。本研究在带惯性权重的粒子群算法中集成了改善全局搜索性能的方法,融入遗传交叉机制以使性能低劣的粒子得到进化,从而提高整个群体的全局优化搜索性能。
3.1 空间优化粒子群算法模型
一个设施k的位置可表示为(xk,yk),对优化的n个设施空间位置问题,粒子群中一个粒子个体表示了对n个设施的一种空间布局试探方案,每个粒子具有n个设施位置分量,粒子位置可表示为(s1,s2,…,sn),其中sk为设施k的坐标点。由于每个点又有x和y两个坐标分量,所以每个粒子的坐标分量有2n个,算法优化时粒子在2n维空间飞行,粒子的位置向量可表示为(x1,y1,x2,y2,…,xn,yn)。如果考虑不同的粒子个体,则粒子i的位置向量表示为(xi1,yi1,xi2,yi2,…,xin,yin),粒子i的速度向量可表示为粒子i的历史最好位置表示为(pi1,pi2,…,pin),整个群体或邻域子群的历史最好位置表示为(pg1,pg2,…,pgn)。由此对带惯性权重的粒子群优化算法的速度迭代模型和位置迭代模型调整如下
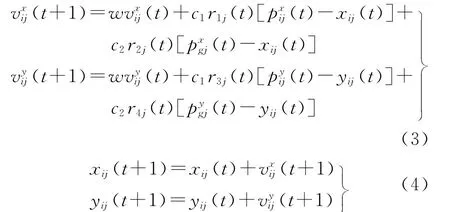
3.2 融入遗传交叉机制
粒子群算法在每一次迭代对所有粒子的速度和位置更新前,先对所有粒子在其当前位置处的适应值按从优到劣进行排序,对前80%适应值较好的粒子按标准粒子群算法速度和位置模型更新,对其余20%适应值较差的粒子按遗传交叉机制更新。算法在适应值较好的粒子中随机选择出占群体总数20%的粒子,通过将它们随机地两两交叉,产生的相同数量后代粒子取代群体中适应值较差的粒子,以使这些粒子搜索能力得到进化,同时增强整个粒子群体脱离局部最优的能力。
用a和b表示被选择的两个参与交叉的个体指针,通过交叉算法由两个父代个体产生子代个体位置和飞行矢量的计算公式表示如下[14]
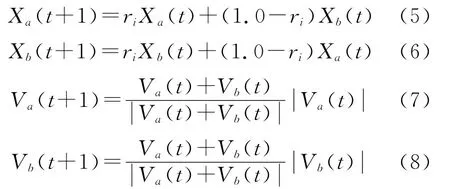
式中,ri~(U(0,1)。经过交叉操作,由两个父代粒子的位置按随机的遗传比例产生了两个子代粒子的位置,速率交叉只有方向受到影响,数量没有变化。
3.3 粒子位置分量飞行空间的设计
网络连续型最大覆盖模型中的所有待优化设施可以布设在网络路段上的任意位置。在粒子群算法中,直接在连续的网络路段轨迹空间中设计设施位置的飞行操作非常困难。考虑到网络上布局的设施与周围需求分布强度的空间关联性,即二维空间分布的需求强度对布设设施具有引力,为了使粒子群优化算法的飞行导向启发机制与寻优性能得以保持和发挥,本文预先建立道路网络空间与二维平面空间之间映射关系,通过构建道路路段的广义Voronoi图实现这种映射。优化算法让粒子个体的每个设施位置分量在二维空间飞行,当某个设施位置飞入到某条路段的Voronoi多边形内部时,该条路段上的最近点即为该设施对应的当前网络空间飞行位置。这种转换机制确保了在高维空间飞行粒子的各个设施位置在网络空间连续飞行,配合粒子群算法使优化进程朝正确的方向拓展,从而实现网络上的连续空间优化。
4 空间优化计算与结果分析
4.1 试验数据与优化参数
本试验对南京市主城区14个消防设施的位置使用最大覆盖模型进行空间优化,优化目标为覆盖尽可能多的城区人口和最小化重叠覆盖,即在限定资源前提下最大限度提高公共安全设施的配置与利用效率。由于获取更详细人口分布资料的限制,本试验以南京市主城各行政区属街道区域为人口的最小统计单位,行政街道区域单元内的人口密度视为均匀分布,以此作为空间优化试验区内需求强度非均匀分布的依据。本试验的网络分析采用路径长度距离作为连接代价,消防设施完全覆盖区域设置为网络路径距离2.5km以内,超过该距离设施功能呈逐步衰减的部分覆盖。优化算法的群体规模设置为50,最大迭代次数为1 500次,速度惯性权重初值1.0、终值0.5。对迭代中每个粒子表示的14个设施的一种布局试探方案,通过计算相应的网络Voronoi面域图,获取各设施覆盖的需求信息,通过模型计算其适应值,当一轮迭代所有粒子的适应值获得后,按照改进的粒子群算法粒子更迭机制进化整个粒子种群。在空间优化计算的迭代过程中,为评估所有产生的粒子所表示的各种设施布局方案性能,共需计算生成75 000幅网络Voronoi面域图。
4.2 优化结果分析
图1分别给出了为采用网络Voronoi面域图分析的优化前后设施的最大覆盖区域。从分图(a)可以看出,现有设施布局功能重叠覆盖严重,同时又存在较大面积未被消防功能完全覆盖的区域。从分图(b)和分图(c)中可以看出,优化布局后的设施主要布设在人口稠密区域,人口密度较低地区和风景区基本未被空间优化出的设施功能覆盖。存在其他未被覆盖的区域主要反映出优化设施趋向于布设在路网和人口密度均比较高的区域,以获得最大的覆盖效率,同时也反映出现有消防站数量不能满足对主城区人口的完全功能覆盖。
表1列出了优化前后按完全覆盖人口排序的南京市主城区14个消防设施功能的完全覆盖面积、完全覆盖人口、综合覆盖人口(含部分覆盖)、网络Voronoi图辐射域人口,图2反映现有设施和优化设施完全覆盖人口对比。可以看出,大部分优化后的设施比现有设施覆盖更多人口,优化后的设施合计完全覆盖人口185.74万,占主城区人口的79.17%,比现有设施完全覆盖人口提高32.18万,增幅达21%;综合覆盖人口由优化前的186.68万提高到优化后的213.72万,增幅达14.5%。图3为本次优化试验过程模型目标函数值变化曲线。
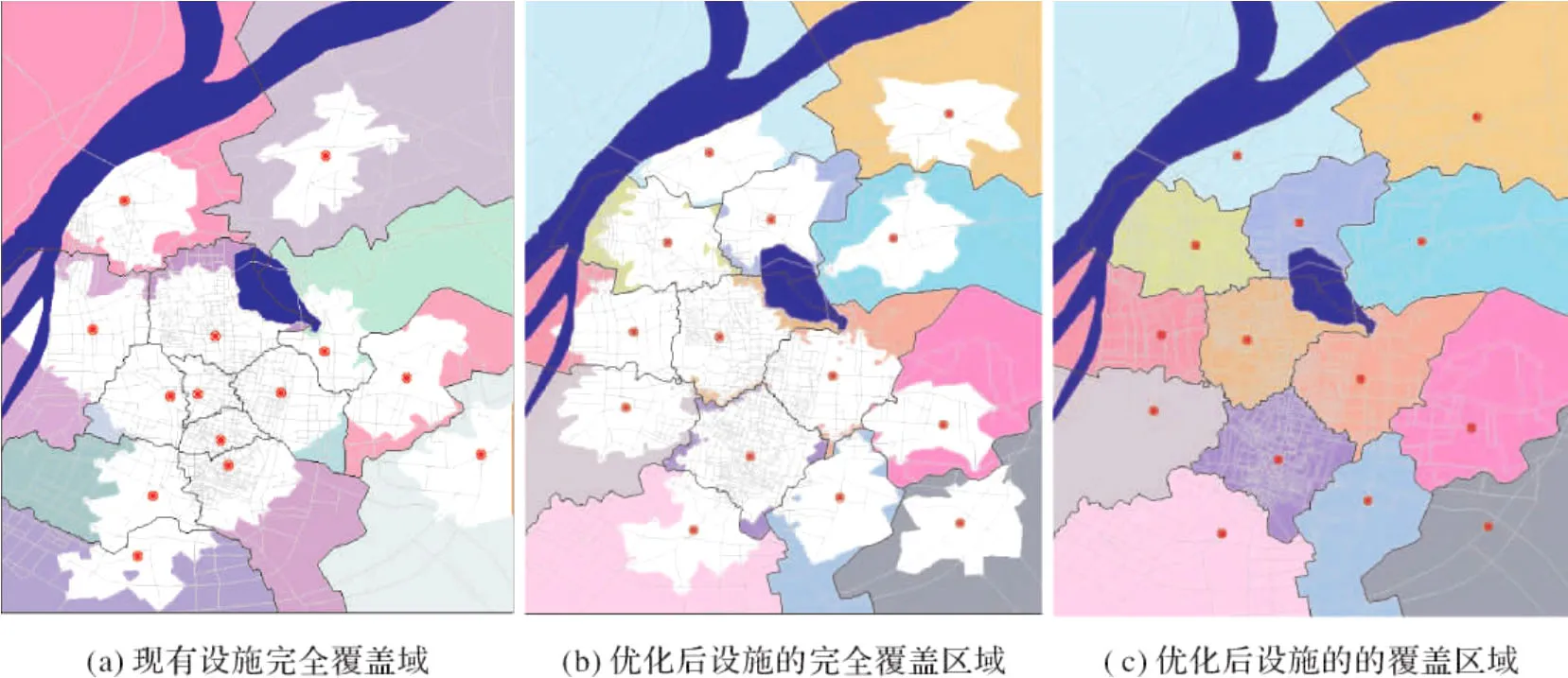
图1 网络Voronoi面域图分析的现有设施和优化设施的完全覆盖域Fig.1 Fully covering areas of present facilities and optimized facilities analyzed by NVAD
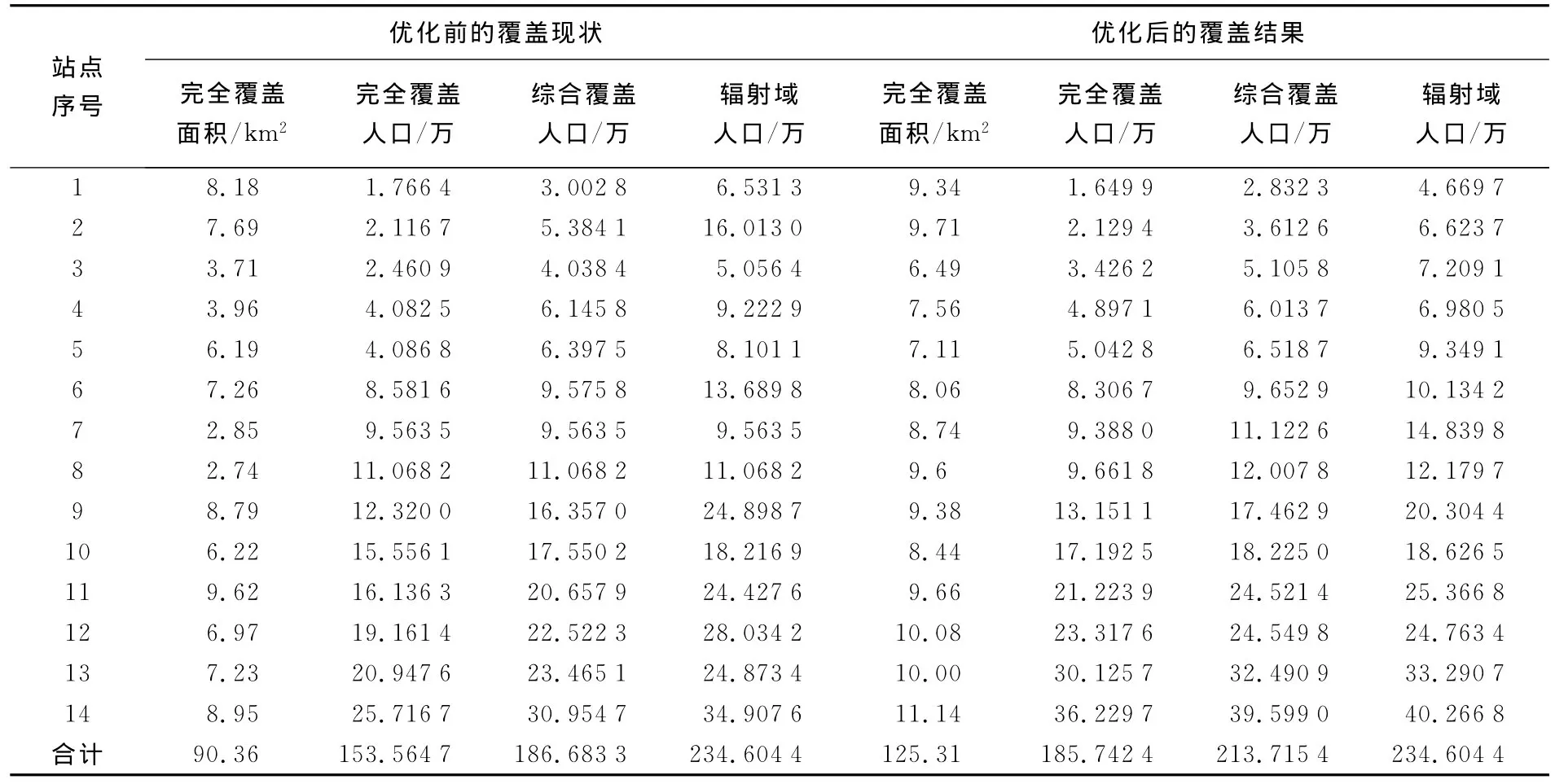
表1 南京市现有设施和优化设施覆盖信息Tab.1 Covering information of present facilities and optimized facilities in Nanjing
为比较网络Voronoi面域图启发式、常规Voronoi图启发式和圆形缓冲区需求分析对最大覆盖空间优化效果的影响,本文分别对基于后两种情形的最大覆盖模型也进行了空间优化试验,并统一采用能够真实反映城市化区域设施需求覆盖效果的网络Voronoi面域图对三种优化获得的设施布局进行评估(表2)。可以看出,基于网络Voronoi面域图启发式优化获得了功能对需求最高的完全覆盖和综合覆盖,常规Voronoi图启发式优化因未考虑道路对功能覆盖的影响,使得优化得到的设施布局实际覆盖的需求低于前者和常规Voronoi图评估结果,同样,通过圆形缓冲区分析的优化既忽略道路影响,又可能包含重叠覆盖统计,对其优化的设施布局进行基于网络环境的评估自然不够理想。

图2 优化前后设施完全覆盖人口对比Fig.2 Contrast of fully covering population of present facilities and optimized facilities

图3 粒子群优化过程目标函数变化曲线Fig.3 Change of object function in particle swarm optimization process

表2 网络Voronoi面域图评估的不同最大覆盖模型优化结果比较Tab.2 Comparison of spatial optimization results based on different maximal covering location models estimated by NVAD
5 结 论
城市化区域多设施最大覆盖科学选址是复杂的空间优化问题,需要对城市空间作用机制的真实模拟和更强的启发式性能,新型空间分析模型、空间选址模型和计算智能方法的结合将成为趋势。城市公共服务设施使用效率的最大化对优化公共资源配置、追求公共服务公平性具有重要的实现意义。本文提出了基于网络Voronoi面域图启发式的最大覆盖选址模型,并结合改进粒子群空间优化方法进行了较为深入的研究,获得如下结论:
(1)基于网络Voronoi面域图的最大覆盖模型具有启发最小化重叠覆盖、最大化覆盖需求的功能,模型顾及完全覆盖和部分覆盖,可以在有限资源条件下,充分发挥城市化区域设施的配置与利用效率。
(2)网络Voronoi图启发式与群智能启发式相结合,可形成两种启发式功能优势互补的技术集成,为产生更强的启发式创造了条件,有益于增强解决复杂的空间优化问题的能力。
(3)将遗传进化机制引入粒子群算法,可以提高算法的全局优化性能,广义Voronoi图能够实现布局设施位置飞行由二维空间到网络空间的转换,为解决复杂的网络连续空间优化提供支持。
(4)试验区现有消防站空间布局不尽合理,功能重叠覆盖严重且存在较大服务盲区,消防站数量不足,通过空间优化,可大幅提高现有消防设施的利用效率。
本研究提出的最大覆盖模型和改进粒子群优化算法可应用于支持城市化区域公共安全和应急救护等服务设施的最大覆盖空间优化决策。当然,本研究还存在一些不足和需要改进的方面,如采用地统计与空间分析结合的方法获得更详细的需求分布数据;根据某些设施的特点,可以考虑采用基于需求出发的网络Voronoi功能吸引域分析与启发的最大覆盖模型;优化过程需要的计算开销较大,仍需进一步改进和提高图形计算和优化计算的效率;进一步开展基于网络路径时间代价分析的空间优化研究。
[1] SUZUKI A,DREZNER Z.The p-center Location Problem in an Area[J].Location Science,1996(4):69-82.
[2] OKABLE A,SUZUKI A.Locational Optimization Problems Solving through Voronoi Diagrams[J].Europe Journal Operation Research,1997(98):445-456.
[3] CHEN Jun,ZHAO Renliang,QIAO Chaofei.Voronoi Diagram-based GIS Spatial Analysis[J].Geomatics and Information Science of Wuhan University,2003,28(Special Issue):32-37.(陈军,赵仁亮,乔朝飞.基于Voronoi图的GIS空间分析研究[J].武汉大学学报:信息科学版,2003,28(特刊):32-37.)
[4] DAVOODI M,MOHADES A,REZAEI J.Solving the Constrained p-center Problem Using Heuristic Algorithms[J].Applied Soft Computing,2011(11):3321-3328.
[5] DAVOODI M,MOHADES A.Solving the Constrained Coverage Problem[J].Applied Soft Computing,2011(11):963-969.
[6] CAVALIER T M,CONNER W A,DE CASTILLO E,et al.A Heuristic Algorithm for Minimax Sensor Location in the Plane[J].European Journal of Operational Research,2007(183):42-55.
[7] ZHU Weining,MA Jingsong,HUANG Xingyuan,et al.A Study of GIS Spatial Competition Analysis Model Based on Projective Weighted Voronoi Diagrams[J].Acta Geodaetica et Cartographica Sinica,2004,33(2):146-150.(朱渭宁,马劲松,黄杏元,等.基于投影加权Voronoi图的GIS空间竞争分析模型研究[J].测绘学报,2004,33(2):146-150.)
[8] OKABLE A,SATOH T,FURUTA T,et al.Generalized Network Voronoi Diagrams:Concepts,Computational Methods and Applications[J].International Journal of Geographical Information Science,2008,22(9),965-994.
[9] OKABLE A,OKUNUKI K.A Computational Method for Estimating the Demand of Retail Stores on a Street Network and Its Implementation in GIS[J].Transactions in GIS,2001,5(3):209-220.
[10] WANG Xinsheng,YU Ruilin,JIANG Youhua.Delimitating the Store Market Field Based on the Metric of the Cityblock Distance[J].Geographical Research,2008,27(1):85-92.(王新生,余瑞林,姜友华.基于道路网络的商业网点市场域分析[J].地理研究,2008,27(1):85-92.)
[11] XIE Shunping,FENG Xuezhi,LU Wei.Algorithm for Constructing Voronoi Area Diagram Based on Road Network Analysis[J].Acta Geodaetica et Cartographica Sinica,2010,39(1):88-94.(谢顺平,冯学智,鲁伟.基于道路网络分析的Voronoi面域图构建算法[J].测绘学报,2010,39(1):88-94.)
[12] XIE Shunping,FENG Xuezhi,WANG Jiechen,et al.Research for Radiation Domain of Commercial Centers in Nanjing Based on Analysis of Road Network Weighted Voronoi Diagram[J].Acta Geographica Sinica,2009,64(1):1467-1476.(谢顺平,冯学智,王结臣,等.基于道路网络加权Voronoi图分析的南京市商业中心辐射域研究[J].地理学报,2009,64(12):1467-1476.)
[13] KENNEDY J,EBERHART R C.Particle Swarm Optimization[C]∥Proc of IEEE International Conference on Neural Networks.Perth:IEEE,l995:1942-1948.
[14] ZENG Jianchao,JIE Jing,CUI Zhihua.Particle Swarm Optimization[M].Beijing:Science Press,2004.(曾建潮,介婧,崔志华.微粒群算法[M].北京:科学出版社,2004.)
[15] DU Guoming,CHEN Xiaoxiang,LI Xia.Spatial Optimal Search Based on Particle Swarm Optimization[J].Acta Geographica Sinica,2006,61(12):1290-1298.(杜国明,陈晓翔,黎夏.基于粒子群优化算法的空间优化决策[J].地理学报,2006,61(12):1290-1298.)
[16] LI Haibo,LI Xia,LIU Xiaoping,et al.Particle-swarm Optimization for Site Selection with Contiguity Constraints[J].Journal of Remote Sensing,2008,12(5):724-733.(黎海波,黎夏,刘小平,等.多目标粒子群算法与选址中的形状优化[J].遥感学报,2008,12(5):724-733.)
[17] YAPICIOGLU H,SMITH A E,DOZIER G.Solving the Semi-desirable Facility Location Problem Using Bi-objective Particle Swarm[J].European Journal of Operational Research,2007(177):733-749.
[18] CHURCH R L,REVELLE C S.The Maximal Covering Location Problem[J].Papers of the Regional Science Association,1974(32):101-118.
[19] ALEXANDRIS G,GIANNIKOS I.A New Model for Maximal Coverage Exploiting GIS Capabilities[J].European Journal of Operational Research,2010(202):328-338.
[20] MURRAY A T,O’KELLY M E,CHURCH R L.Regional Service Coverage Modeling[J].Computers &Operations Research,2008(35):339-355.
[21] BERMAN O,DREZNER Z,KRASS D,et al.The Variable Radius Covering Problem[J].European Journal of Operational Research,2009(196):516-525.
[22] BERMAN O,DREZNER Z,KRASS D.Generalized Coverage:New Developments in Covering Location Models[J].Computers &Operations Research,2010(37):1675-1687.
[23] MURAWSKI L,CHURCH R L.Improving Accessibility to Rural Health Services:The Maximal Covering Network Improvement Problem[J].Socio-economic Planning Sciences,2008(43):102-110.
[24] MA Yunfeng,YANG Chao,ZHANG Min,et al.Timesatisfaction-based Maximal Covering Location Problem[J].Chinese Journal of Management Science,2006,14(2):45-51.(马云峰,杨超,张敏,等.基于时间满意的最大覆盖选址问题[J].中国管理科学,2006,14(2):45-51.)
Maximal Covering Spatial Optimization Based on Network Voronoi Diagrams Heuristic and Swarm Intelligence
XIE Shunping,FENG Xuezhi,DU Jinkang
School of Geographic and Oceanographic Scienses,Nanjing University,Nanjing210093,China
A maximal covering location model based on network Voronoi area diagrams and particle swam optimization is proposed to provide the spatial optimization means for response sensitive public service facilities in urbanized area.It is taken into account that facilities function conducts along traffic network and variable demands distribute continuously,the facilities optimized can be located in continuous network space.The network Voronoi area diagrams are used to simulate the service areas of facilities in the maximal covering location model,which has heuristic to minimize overlap coverage in spatial optimization.The proposed model maximizes utilization of facilities,the demands within coverage radius are covered completely and the demands beyond coverage radius are covered partially by facilities function.An improved particle swam optimization algorithm integrated with genetic mechanism and generalized Voronoi diagram is proposed to enhance the optimization performance in continuous network space.The computational experiment for location optimization of fire stations in Nanjing shows that the proposed model and optimization algorithm have achieved desired results.
network Voronoi area diagram;spatial optimization;maximal covering location model;Voronoi diagrams heuristic;particle swarm optimization
XIE Shunping(1957—),male,PhD,senior engineer,majors in theory and application of GIS,spatial analysis and intelligent spatial optimization.
1001-1595(2011)06-0778-07
P208
A
国家863计划(2008AA12Z106)
丛树平)
2011-03-11
2011-09-20
谢顺平(1957—),男,博士,高级工程师,研究方向为地理信息系统理论与应用、空间分析与智能空间优化。
E-mail:xiesp@nju.edu.cn
