卫星遥感影像有理函数模型优化方法

张永军，王 蕾，2，鲁一慧

1.武汉大学遥感信息工程学院，湖北武汉430079；2.四川测绘局第三测绘工程院，四川成都610500

卫星遥感影像有理函数模型优化方法

张永军1，王 蕾1，2，鲁一慧1

1.武汉大学遥感信息工程学院，湖北武汉430079；2.四川测绘局第三测绘工程院，四川成都610500

针对高分辨率遥感影像有理函数模型（RFM）在实际应用中存在过度参数化和定位精度不高的问题，提出基于离差阵和消去变换及残余系统误差补偿的高分辨率遥感影像RFM优化方法。试验结果表明，经过参数筛选后的RFM参数均为无偏估计值，拟合精度可以达到全部参数用于拟合时的精度，而且模型病态性基本消除，模型稳定性更高。残余系统误差补偿方法可以有效消除RFM拟合严格成像模型的残余误差，达到与严格成像模型一致的对地定位精度。

高分辨率卫星影像；有理函数模型；离差阵；消去变换；病态问题；残余系统误差

1 前 言

随着航天测图技术的不断发展和广泛应用，高分辨率卫星遥感影像的摄影测量处理理论和应用技术引起了国际摄影测量界的普遍关注［1－2］。有理函数模型（rational function model，RFM）作为一种通用的传感器成像模型，形式简单，计算速度快，更具一般性和保密性，自2000年以来迅速成为研究热点［3－10］，目前大部分高分辨率遥感卫星运营商均采用该模型作为传感器成像模型。然而RFM作为严格成像模型的拟合模型，在理论研究和实际应用中凸现出许多亟待解决的问题：①模型参数求解存在病态问题［11－12］；②高阶RFM因参数过多导致解不稳定［13］；③ 采用有理函数拟合严格成像模型时存在较为明显的残余误差［8］。

针对RFM拟合严格成像模型存在过度参数化的问题，目前国内外主要从算法改进和模型构造两个方面进行研究，例如采用岭估计等方法改善有理多项式系数（rational polynomial coefficients，RPC）求解过程中法方程的状态［11］或略去RFM的三次项［13］。但是，岭估计等方法不能彻底解决过度参数化问题，且用二次RFM拟合严格成像模型没有分析每个参数的显著性，理论上不严密。

事实上，利用RFM“代替”严格成像模型进行对地定位时，其系统误差可以分为严格成像模型本身存在的系统误差和利用RFM拟合严格模型的残余系统误差两类。目前提高RFM定位精度的方法都是利用地面控制点进一步优化RFM参数，并未将严格成像模型本身存在的系统误差和由RFM模型局限性造成的残余系统误差区别处理。

本文结合参数显著性检验理论，提出基于离差阵逐步回归的RFM参数筛选求解方法，减少RFM拟合严格成像模型的参数个数，解决RFM过度参数化问题，同时提出一种无需地面控制点的RFM残余系统误差改正方法，提高无地面控制点情况下的对地定位精度。

2 基于离差阵的RFM参数逐步筛选求解

RFM的一般形式如式（1）所示［7］

式中，（P，L，H）表示正则化的地面坐标，（Sr，Sc）表示正则化的影像坐标，NumL（P，L，H）、DenL（P，L，H）、NumS（P，L，H）及DenS（P，L，H）分别为下列三阶多项式

式中，a0，…，b19，c0，…，d19为有理多项式系数，即RFM未知数，通常取b0＝1，d0＝1。

设有n组观测数据，则上述模型可以用矩阵形式表达为［7］

令式（2）和式（3）的系数矩阵为X，其元素为xi1，…，xim（i＝1，2，…n），ri（i＝1，2，…n）为线性方程组的常数项，m为未知数个数，n为观测方程个数。分别对上述两式构造m＋1阶离差阵式（4），采用消去变换法［14］求解未知参数的无偏估计并在计算中消去多余参数，优化回归模型，即可获得无偏的最优解算结果。下面以式（2）中参数a0到b19的计算为例进行分析说明。

令m＋1阶离差阵A（0）为

式中

通过参数显著性检验判断参数项是否可以被选入模型，计算各个自变量的偏回归平方和

（1）判断不在模型中的变量可否引入时，设

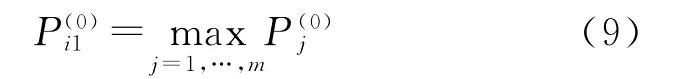
检验H0：βi1＝0（即变量Xi1对r的作用是否显著），检验统计量为［14］

式中，Q（i1）表示在原有参数基础上选入Xi1时的残差平方和。给定显著性水平α1，记自由度为n－2的F分布临界值为若Fin（1，n－2），则引入变量Xi1，并对以该变量为主元的离差阵作消去变换，否则停止筛选。

（2）设t为已引入的变量个数，判断已在模型中的变量可否剔除时，设

检验变量Xi0可否剔除的检验统计量为［14］

式中，Q（i1，…，it）表示已选入Xi1，…，Xit时的残差平方和。给定显著性水平α2，记自由度为n－t－1的F分布临界值为Fout（1，n－t－1），若≤Fout（1，n－t－1），则剔除变量Xi0，并对以该变量为主元的离差阵作消去变换，然后继续检验模型中的变量可否剔除；否则考虑能否引入新变量。

假定筛选变量结束后，引入方程的变量个数为h（h≤m），记为Xi1，…，Xih，A（0）经过h次消去变换后转化为

由A（h）即可得到回归分析中的所有结果。

3 RFM残余系统误差改正

研究表明，利用卫星影像辅助文件提供的RPC参数，无论是物方还是像方定位误差都具有很强的系统性，并且误差主要随纬度或影像行（卫星运动前进方向）的变化而变化［15］。许多利用SPOT－5和IKONOS卫星影像提供的RPC分析定位误差同样呈现相似的系统性。本文利用SPOT－5卫星参数和严格成像模型生成虚拟控制点格网并采用RFM拟合严格成像模型，两组试验数据的像方坐标残余误差分布如图1所示。可以看出，利用RFM拟合严格成像模型的残差呈现明显而有规律的系统性，最大残差分别达到0.1和0.05像素，且系统误差主要随影像行的变化而变化，与已有研究成果的试验结论相似，说明残余系统误差分布呈现普遍性。

本文提出的RPC残余系统误差补偿方法与摄影测量中系统误差处理的间接补偿法类似，结合了自检校法和验后补偿法的优点，不需要地面控制点，不改变原有平差程序，通过先验知识构造较为通用的残余系统误差补偿模型，直接嵌入RPC逐步筛选求解的过程中，利用RPC残差值求出残余系统误差模型参数，从而提高定位精度。

图1 利用RFM拟合严格成像模型后的像点残差分布Fig.1 Image point residues after RFM interpolation

利用残余误差主要随影像行变化而变化，变化趋势呈现波状分布的先验知识，通过试验，在傅里叶系数和高次项系数中（其他方法在拟合时均出现不足）选用拟合效果较好的傅里叶系数构造残余系统误差模型式（14），式中ΔSr和ΔSc即为残余系统误差改正模型。由于像点坐标Sr和Sc相互独立，残差分布也不相同，因此需要分别改正。

式中

式中，pr0、pr1、…、qr5、wr为像点坐标Sr方向（卫星轨道运行方向）残余系统误差改正模型系数，pc0、pc1、…、qc4、wc为像点坐标Sc方向残余系统误差改正模型系数。由于Sr方向系统误差比Sc方向系统误差分布复杂，其改正模型也比Sc方向多一对傅里叶系数项。

4 试验结果与分析

本文方法理论上适用于所有高分辨率卫星影像，但由于其他商业卫星影像的严格成像模型未知，因此利用已知严格成像模型的SPOT－5数据进行试验验证，下面采用其中两组数据进行说明。

试验数据1：该数据由基于共线方程的严格成像模型生成，影像大小为12 000×12 000像素。控制点和检查点格网均为5层，交叉分布。最小高程200.000 000m，最大高程2 200.000 000m，地面点坐标精确到小数点后6位。

试验数据2：影像大小为6 000×6 000像素，像点坐标按200×200像素均匀分布。控制点和检查点格网均为11层，交叉分布。最小高程－0.000 003m，最大高程8 999.993 091m，地面点坐标精确到小数点后6位。

地面点采用大地坐标系（L，B，H），单位分别为（°）、（°）、m。

4.1 RFM参数逐步筛选求解

利用本文提出的逐步参数筛选方法求解的RPC参数与利用传统的岭估计方法求解的RPC参数序号对比如表1所示。本文方法将原模型的78个RPC参数经过显著性检验，分别筛选减少为29和32个参数。此外，筛选法求解的RPC未知数中误差比岭估计法求解的未知数中误差要小，精度更高。

表1 参数逐步筛选后保留的RPC未知参数Tab.1 Remained RPC unknowns with the proposed approach

表2是两组数据的RFM求解模型设计矩阵条件数对比，可以看出采用岭估计解算RPC时，设计矩阵条件数比原线性矩阵条件数有所减小，一定程度上改善了模型病态性。利用本文提出的参数筛选方法剔除不显著的RPC参数项后，新模型的设计矩阵条件数非常小，基本克服了原模型求解RPC时存在的病态性问题。

表2 设计矩阵条件数Tab.2 Condition index of the designed matrix

RFM拟合精度直接关系到高分辨率卫星遥感影像处理和数字测图的效果，为了验证利用筛选后的RFM参数是否能达到全部78个参数的拟合效果，表3列出两组试验数据分别利用岭估计法和逐步筛选参数法求解的RPC参数模型的拟合精度。可以看出，利用约30个RPC参数的模型拟合精度与岭估计的78个RPC参数模型拟合精度几乎一致，说明本文方法的正确性和有效性。第一组试验数据的RPC拟合精度较差主要由不同的高程分层数引起，已有大量文献讨论该问题，本文不再赘述。

4.2 RFM残余系统误差改正

利用基于离差阵的参数逐步筛选法求解RFM后，两组试验数据的像点残差如图1所示；采用本文提出的残余系统误差改正方法进一步拟合后的像点残差如图2所示。可以看出，采用RFM拟合严格成像模型时，像点残差大小分布呈现明显的系统性，主要随Sr方向（卫星运动前进方向）变化，最大残差达到0.1和0.05像素量级，本文提出的残余系统误差改正方法能够明显提高原模型的拟合精度，可以基本消除像点残差的系统性，最大残差仅为0.05、0.005像素量级，其拟合精度统计如表4所示。可以看出经过残余系统误差改正后，RFM定位精度显著提高，完全可以替代严格成像模型进行卫星遥感影像的对地定位处理。

表3 不同RPC求解方法的拟合精度Tab.3 Precision of RPC using different methods 像素

图2 残余系统误差改正后的像点坐标残差分布Fig.2 Image point residues after correction of remnant systematic errors

表4 残余系统误差改正前后的拟合精度对比Tab.4 Precision comparison between precision before and after remnant systematic error correction 像素

5 结 论

本文提出基于离差阵和消去变换的RFM未知参数逐步筛选求解方法，用最少最合理的参数项拟合卫星遥感影像的严格成像模型，克服过度参数化导致的系统病态性，并提出一种RFM残余系统误差的补偿方法。

试验结果表明，利用分母不相同的三阶RFM拟合严格成像模型，参数间的复共线性导致模型系统病态，参数解不稳定。本文提出的逐步筛选参数求解方法可以解决RFM拟合严格成像模型的过度参数化问题。该方法优化了数学模型，可以获得最小二乘无偏估计结果，且模型稳定性比岭估计方法高。该方法的参数个数虽然减少一半以上，但拟合精度与原78个参数模型的拟合精度一致。

RFM拟合严格成像模型时存在主要随卫星轨道运行方向变化的残余系统误差，利用本文提出的残余系统误差补偿方法可以有效消除该残余误差，拟合精度大大提高。

在实际应用中，基于离差阵的RFM参数逐步筛选方法和RFM残余系统误差的改正方法可以独立或结合使用，例如拟合RFM时可以采用逐步筛选法进行解算，当残余系统误差较大时再采用残余系统误差补偿方法提高拟合精度。

［1］ WANG J，DI K，LI R.Evaluation and Improvement of Geopositioning Accuracy of IKONOS Stereo Imagery［J］.ASCE Journal of Surveying Engineering，2005，131（2）：35－42.

［2］ ZHANG Yongjun，ZHANG Yong.Direct Geo－referencing of SPOT 5HRS Imagery without（or with a Few）Ground Control Point［J］.Geomatics and Information Science of Wuhan University，2005，31（11）：941－944.（张永军，张勇.SPOT 5HRS立体影像无（稀少）控制绝对定位技术研究［J］.武汉大学学报：信息科学版，2005，31（11）：941－944.）

［3］ GRODECKI J.IKONOS Stereo Feature Extraction－RPC Approach［C］∥Proceedings of the ASPRS Annual Conference.St Louis：［s.n.］，2001：23－27.

［4］ TAO C V，HU Y.A Comprehensive Study on the Rational Function Model for Photogrammetric Processing［J］.Photogrammetric Engineering and Remote Sensing，2001，67（12）：1347－1357.

［5］ TAO C V，HU Y.3－D Reconstruction Algorithms with the Rational Function Model and Their Applications for IKONOS Stereo Imagery［C］∥Proceedings of Joint ISPRS Workshop on High Resolution Mapping from Space.Hannover：［s.n.］，2001.

［6］ FRASER C S，HANLEY H B.Bias Compensation in Rational Functions for IKONOS Satellite Imagery［J］.Photogrammetric Engineering and Remote Sensing，2003，69（1）：53－57.

［7］ GRODECKI J，DIAL G.Block Adjustment of High－resolution Satellite Images Described by Rational Functions［J］.Photogrammetric Engineering and Remote Sensing，2003， 69（1）：59－68.

［8］ FRASER C S，HANLEY H B.Bias－compensated RPCs for Sensor Orientation of High－resolution Satellite Imagery［J］.Photogrammetric Engineering ＆Remote Sensing，2005，71（8）：909－915.

［9］ FRASER C S，DIAL G，GRODECKI J.Sensor Orientation via RPCs［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2006，60（3）：182－194.

［10］ TONG X H，LIU S J，WENG Q H.Bias－corrected Rational Polynomial Coefficients for High Accuracy Geopositioning of QuickBird Stereo Imagery［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2010，65（2）：218－226.

［11］ YUAN Xiuxiao，LIN Xianyong.A Method for Solving Rational Polynomial Coefficients Based on Ridge Estimation［J］.Geomatics and Information Science of Wuhan University，2008，33（11）：1130－1133.（袁修孝，林先勇.基于岭估计的有理多项式参数求解方法［J］.武汉大学学报：信息科学版，2008，33（11）：1130－1133.）

［12］ GUI Qingming，YAO Shaowen，GU Yongwei，et al.A New Method to Diagnose Multicollinearity Based on Condition Index and Variance Decomposition Proportion［J］.Acta Geodaetica et Cartographica Sinica，2006，35（3）：210－214.（归庆明，姚邵文，顾勇为，等.诊断复共线性的条件指标－方差分解比法［J］.测绘学报，2006，35（3）：210－214.）

［13］ ZHAO Liping，LIU Fengde，LI Jian，et al.Research on Reducing Term of Higher Order in RFM Model［J］.Science of Surveying and Mapping，2007，32（4）：14－17.（赵利平，刘凤德，李健，等.减少有理函数模型中高次项的初步研究［J］.测绘科学，2007，32（4）：14－17.）

［14］ GAO H uixuan.Application of M ultiple Statistical Analyses［M］.Beijing：Press of Peking University，2005.（高惠璇.应用多元统计分析［M］.北京：北京大学出版社，2005.）

［15］ TONG Xiaohua，LIU Shijie，YE Qin.Accuracy Analysis and Improvement of QuickBird Stereo Positioning Based on Rational Function Model［J］.Journal of Tongji University：Natural Science，2009，37（4）：555－559.（童小华，刘世杰，叶勤.基于有理函数模型的QuickBird立体定位精度分析［J］.同济大学学报：自然科学版，2009，37（4）：555－559.）

Optimization of the Rational Function Model of Satellite Imagery

ZHANG Yongjun1，WANG Lei1，2，LU Yihui1
1.School of Remote Sensing and Information Engineering，Wuhan University，Wuhan 430079，China；2.The Third Surveying and Mapping Institute of Sichuan Surveying and Mapping Bureau，Chengdu 610500，China

To solve the problems of over－parameterization and low geo－referencing accuracy of rational function model（RFM），a novel method of parameter optimization based on scatter matrix and elimination transformation and a new method of remnant systematic error compensation without ground control points are proposed.The proposed parameter optimization method can resolve the ill－posed problem of RFM by rejecting all excess parameters.The systematic error compensation method introduces a new correction model with Fourier coefficients.Experimental results indicate that the performance of the proposed method with less parameters is equal to that of the conventional model with all of the 78 parameters.Moreover，the ill－posed problem is effectively eliminated and thus the stabilities of estimated parameters are improved.The systematic error compensation scheme significantly eliminates the remnant systematic error of RFM and improves the geo－referencing accuracy.

high－resolution satellite imagery；rational function model；scatter matrix；elimination transformation；ill－posed problem；remnant systematic error

1001－1595（2011）06－0756－06

P237

A

国家自然科学基金（41071233；40671157）

丛树平）

2010－07－09

2011－04－27

张永军（1975—），男，博士，教授，博士生导师，研究方向为数字摄影测量与遥感、计算机视觉等。First author：ZHANG Yongjun（1975—），male，PhD，professor，PhD supervisor，majors in digital photogrammetry and remote sensing，computer vision.

E－mail：zhangyj＠whu.edu.cn