基于空域最小二乘法求解GOCE卫星重力场的模拟研究
2011-01-04徐新禹李建成姜卫平邹贤才
徐新禹,李建成,姜卫平,邹贤才
1.武汉大学测绘学院,湖北武汉430079;2.武汉大学地球空间环境与大地测量教育部重点实验室,湖北武汉430079
基于空域最小二乘法求解GOCE卫星重力场的模拟研究
徐新禹1,2,李建成1,2,姜卫平1,2,邹贤才1,2
1.武汉大学测绘学院,湖北武汉430079;2.武汉大学地球空间环境与大地测量教育部重点实验室,湖北武汉430079
论述最小二乘过程中有色噪声的处理方法,提出使用自回归模型对GOCE梯度观测值中的有色噪声进行时域滤波,数值模拟结果验证该方法的有效性。利用数值模拟验证直接求逆方法和PCCG法求解大型法方程的有效性,后者的效率远远高于前者。联合加入噪声(有色噪声和白噪声)的卫星重力梯度张量径向分量观测值Vzz和SST观测值,分别使用空域最小二乘法和半解析法恢复180阶全球重力场模型,前者求解重力场模型的大地水准面和重力异常在180阶次的精度分别为3.01 cm和0.75 mGal(1 mGal=10-5m/s2),优于半解析法求解模型的精度。
GOCE卫星;空域最小二乘法;预处理共轭梯度法;半解析法;卫星重力梯度;自回归模型
1 引 言
21世纪初成功实施的CHAMP(challenging minisatellite payload)和GRACE(gravity recovery and climate experiment)卫星重力探测计划以前所未有的精度获得了重力场的中、长波信息,为实现本世纪大地测量的宏伟目标——厘米级大地水准面奠定了坚实的基础[1]。但由于已实施的卫星重力探测模式以及重力场信号随高度上升快速衰减特性的限制,恢复重力场模型的精度和分辨率仍然很难满足许多地球相关学科的科学目标需求[2]。ESA负责实施的GOCE(gravity field and steady-state ocean circulation explorer)卫星于2009年3月17日成功发射(http:∥www.esa. int/esaLP/ESAYEK1VMOC_LPgoce_0.html),其采用SGG(satellite gravity gradiometry)技术和SST-hl(satellite-to-satellite tracking in the high-low mode)技术相结合的测量模式,SGG技术的观测量为引力位的二阶导数,能在一定程度上补偿重力场信号随高度产生的衰减,因此期望获得更高精度和分辨率的重力场模型[3]。
自20世纪70年代以来,国内外学者和机构对利用卫星重力梯度观测值恢复地球重力场的相关理论与方法进行了大量的研究,并进行了大量的数值分析与验证[4-15],主要是从空域法和时域法出发讨论。空域法把观测值看做位置的函数,其解算方法主要有积分法、最小二乘配置法、最小二乘谱组合法、空域最小二乘法[4-5]。时域法是将观测值看做沿轨道的时间序列,使用倾角函数表示球谐函数,解算方法一般有两种:时间域时域法和半解析法(semi-analytical,SA)[4-5,9,11]。空域最小二乘法直接利用沿卫星轨道的观测值建立观测方程,由经典的最小二乘方法求解。该方法不对数据进行归算、格网化等处理,同时不需考虑数据中断、跳跃等问题,因而可获得较精确的结果,并提供求解参数完全的方差-协方差矩阵,是一种较为严密的方法。但该方法在处理海量观测值,且观测值中包含有色噪声时,恢复高阶次重力场模型对计算机性能要求较高。空域最小二乘法是ESA最终利用GOCE卫星任务实测数据确定高精度高分辨率全球重力场的方法之一[13-14]。本文主要研究其由SGG观测数据求解高阶卫星重力场模型的相关理论、方法及算法。
2 数学模型
2.1 引力位的二阶导数
地心球坐标系下引力位的二阶导数f(r,θ,λ)可表示成傅里叶级数形式[5]

式中,

r、θ、λ分别表示地心球坐标的半径、地心余纬(90°-地心纬度φ)、地心经度;n、m是球谐展开的阶和次;¯Cnm、¯Snm是正规化的n阶m次引力位球谐系数;¯Pnm(cosθ)为完全规格化缔合勒让德函数;Afm(r,θ)、Bfm(r,θ)为傅里叶系数;Hfnm(r,θ)为其与引力位系数之间的转换系数,不同引力位函数对应不同形式的傅里叶系数和转换系数。根据局部指北坐标系(x,y,z)的定义(x轴指向北,y轴指向西,z轴径向朝外)及其与地心球坐标(r,θ,λ)之间的关系,可推导出其中引力梯度张量球谐级数展开式中傅里叶系数和转换系数的形式,如表1所示,其中为地球万有引力常数与地球质量的乘积,R是地球平均半径。本文的模拟试算均在局部指北坐标系下进行,该坐标系是GOCE任务实测梯度数据处理中采用的坐标系之一。

表1 局部指北坐标系中引力梯度张量的6个分量所对应傅里叶系数和转换系数的形式Tab.1 Fourier coefficients and transformation coefficients of the six components of gravitational gradient tensor in the local north-oriented coordinate system
2.2 空域最小二乘法的数学模型及有色噪声处理方法
从式(1)可看出卫星引力梯度观测值是卫星位置和重力场模型参数的函数。从严格意义上说,卫星位置和重力场参数都是未知的,因此观测方程是非线性的,在实际使用中需要线性化以便同时求解位置和重力场参数。考虑到GOCE任务的精密定轨技术已经可达厘米水平,经验证5cm的轨道误差对引力梯度张量观测值影响的最大量级为0.04mE,这相对于GOCE卫星重力梯度仪在测量带宽内3mE的精度可忽略不计[3],因此可认为卫星位置已知。在引入正常引力场的情况下,可建立如下观测方程
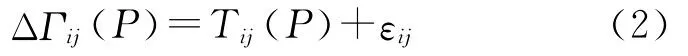
式中,ΔΓij(P)表示引力梯度异常,是引力位梯度与正常位梯度之差;Tij(P)为扰动引力梯度,εij表示观测误差以及模型误差;P表示精密定轨技术确定的卫星位置。式(2)中仅包含重力场位系数参数,可由卫星轨道上每个点的观测值形成方程组,将Tij(P)展开如式(1)的形式,则式(2)对应的线性Gauss-Markov观测模型和统计模型为

式中,y表示梯度观测值向量,既可是引力梯度异常的单个分量,也可是多个分量的组合;A为设计矩阵;x表示位系数参数向量;ε为观测误差向量;为单位权方差;Q为观测值的误差协方差矩阵;P为观测值的权。根据经典线性最小二乘原理可求得式(3)的最优无偏估计解

GOCE任务梯度观测值中包含有色噪声,将导致形成的误差协方差矩阵Q不再是对角阵,且随着观测量的增多,该矩阵维数不断增大,给直接处理协方差矩阵(求逆、乘积等)带来困难,因而需要找到合适的方法处理有色噪声带来的计算问题。根据GOCE任务重力梯度测量误差的特性,误差时间序列为广义平稳随机信号,若假设观测值为周期的等间隔(空间)采样或者为格网点值,则Q是一个循环Toeplitz矩阵,但是Q的逆将破坏其原有的循环Toeplitz结构。若将Q分解为两个三角矩阵的乘积Q=RTR,根据矩阵运算规律(RTR)-1=R-1(R-1)T、式(3)和式(4)可推导出如下法方程


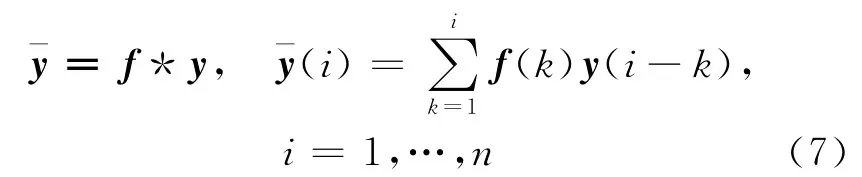
该卷积过程可看做一个离散线性移不变系统,向量f对应滤波器的脉冲响应。该过程可利用FFT算法快速计算(时域卷积在频域内为简单的乘积),首先将时域内的时间序列转换到频域内,滤波后再转换到时域内,该方法可为频域滤波;根据信号处理理论中的相关定理,信号的自相关函数与PSD(power spectral density)成傅里叶变换对,因此还可通过噪声特性构造时域滤波器,例如基于AR(autoregressive)模型的高通滤波器,这样空域最小二乘中有色噪声的处理过程就变成了一个时域滤波过程。
需要指出,求解高阶重力场模型的最小二乘方法非常耗时,尤其是法方程的解算,本文将对直接求逆法和PCCG(preconditioned conjugate gradient)进行模拟比较,前者是对法方程矩阵严格求逆,优点是可以获得参数的方差-协方差矩阵(可表征求解参数的精度),后者通过迭代快速解算法方程,但无法严格给出求解参数的精度信息。
3 数值分析
3.1 滤波方法的分析与验证
为验证基于AR模型的时域滤波方法的有效性,本文基于先验误差PSD模拟了30d5s采样的有色噪声时间序列,其统计特性如表2所示,统计量的单位为E(Eötvös),先验误差PSD的解析形式为[16]

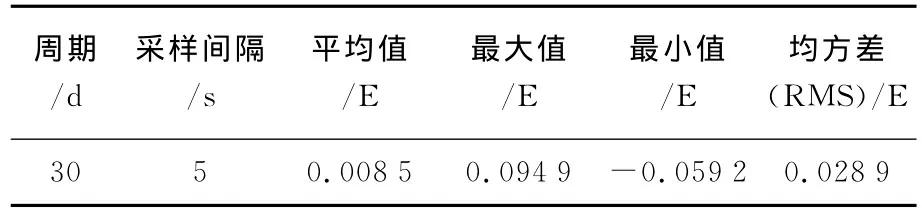
表2 模拟有色噪声误差时间序列的统计结果Tab.2 Statistical results of the simulated colored noise time series
本文取先验误差PSD的倒数来构造AR高通滤波器,AR模型的最高阶取8 640,首先用先验解析形式的误差PSD的倒数计算自相关函数,再利用得到的自相关函数计算AR模型的参数以形成时域滤波器,利用其对模拟的噪声时间序列进行滤波处理,为分析滤波的效果,验证该方法的有效性,图1、图2和图3分别为滤波前后噪声时间序列、分布图和协方差函数图。从图中可明显看出,滤波前噪声时间序列具有一定的相关性,且不具备正态分布特性,时间序列曲线呈现一定的规律性,具有明显的有色噪声特性;滤波后噪声时间序列呈现正态分布,且不存在相关性,其时间序列分布也显示出随机噪声的特性。结果充分说明采用构造的AR滤波器对GOCE梯度观测值有色噪声的滤波非常有效,滤波过程是白噪声化的过程,即消除噪声时间序列的相关性,这与2.2节中的理论分析一致。

图1 滤波前(左)、后(右)的噪声时间序列Fig.1 Noise time series before(left)and after(right)filtering

图2 滤波前(左)、后(右)噪声时间序列的分布Fig.2 Distribution of noise time series before(left)and after(right)filtering
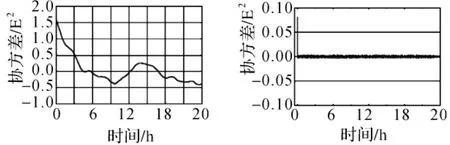
图3 滤波前(左)、后(右)噪声时间序列的协方差函数Fig.3 Covariance function of noise time series before(left)and after(right)filtering
3.2 恢复180阶重力场模型的数值分析
为了分析空域最小二乘法求解GOCE卫星重力场的精度及运行效率,并将其与SA方法进行比较,本文模拟了GOCE任务29d的观测数据,采样间隔为5s,EGM96为轨道模拟的参考模型,轨道倾角约为96.7°,偏心率为0.001,轨道的平均高度为245km,是一个近似重复轨道,选择GFZ发布的EIGEN_CG03C重力场模型模拟引力梯度张量观测值,模型最高阶取至180。SST观测值的模拟采用EIGEN_CG03C模型计算沿模拟卫星轨道的引力位来实现,模型的最高阶为80阶,加入方差为0.5m2s-2的白噪声,其相应于方差为5cm的位置误差和10-4m/s的速度误差。下面的数值分析仅以重力梯度的径向分量Vzz为例,其在引力梯度张量中量级最大,加入有色噪声的统计特性如表2所示。
在使用空域最小二乘法求解地球重力场模型之前,首先对直接求逆法和PCCG方法求解法方程的有效性及软件模块性能进行测试,测试平台为IBM P5-575,该小型机共有24个64位1.9GHz的POWER5CPU,测试数据选用不包含误差的引力梯度张量观测值的径向分量Vzz。需要指出本文所采用的直接求逆法和PCCG方法均是在已形成法方程的基础上进行的,对于由大量的观测数据求解高阶重力场模型来说,形成法方程也是一个非常耗时的过程,根据法方程的计算特性,可采用多线程提高计算效率。基于直接求逆方法和PCCG方法由无误差的观测值求得模型的阶误差均方差如图4所示,图中实线表示EIGEN_CG03C模型的信号阶次方差均方差(下同),点虚线表示直接求逆得到模型的阶误差均方差,短划线虚线表示PCCG方法求得模型的阶误差均方差,前者计算需要约13d,后者仅需30min经过25次迭代即可收敛。需要指出本文求解结果的比较均是相对于EIGEN_CG03C模型,对于模拟试算来说,其相当于“真”实场,阶误差均方差的计算公式为
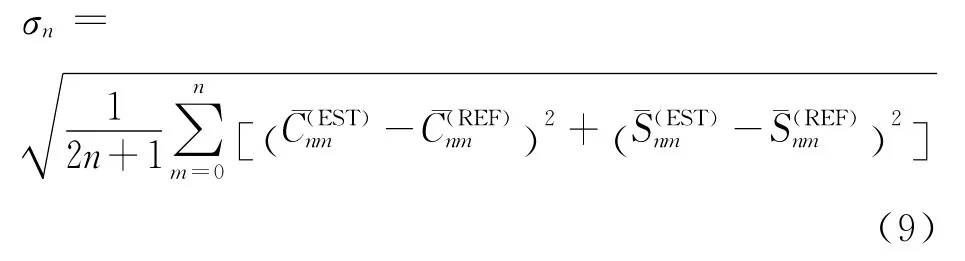
式中,n,m为模型的阶次;上标‘EST’表示求解的重力场模型,‘REF’表示“真”实重力场模型。
从图4中可看出,两种方法均能以较高的精度(10-15~10-13)恢复位系数,求解模型的大地水准面和重力异常误差均方差在纬度±80°范围内量级分别为10-3cm和10-4mGal,在纬度±90°范围内量级分别为10-2cm和10-2mGal,这说明求解结果受到了极区无观测数据的影响,导致求解过程不稳定。从求解结果还可看出直接求逆方法比PCCG方法更精确,但PCCG方法的速度要快很多,虽然精度略有降低,但足以满足求解的精度要求。需要指出,运算中并未使用任何正则化技术,图中的阶误差均方差在接近180阶处有跳跃,应该是高阶重力场数值不稳定性引起的。
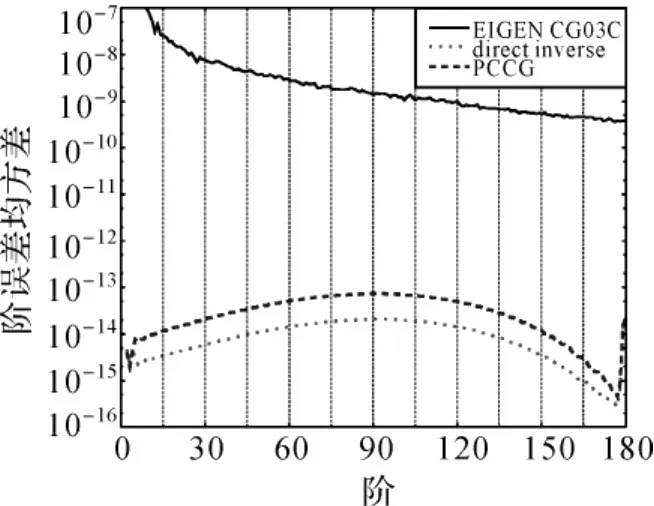
图4 利用直接求逆方法和PCCG方法求得模型的阶误差均方差Fig.4 Degree error RMS of the gravity model estimated from the direct inverse and the PCCG method
基于包含误差(有色噪声和白噪声)的引力梯度张量径向分量Vzz和SST观测值,分别利用SA方法和空域最小二乘法恢复重力场模型的阶误差均方差,如图5所示,其中点虚线表示SA方法求得模型的阶误差均方差,短划线虚线表示采用了AR滤波的空域最小二乘法求得模型的阶均方差,短划线-点虚线表示未采用滤波的空域最小二乘法求得模型的阶均方差,对于GOCE卫星高阶地球重力场的确定,由于极空白、重力场信号向下延拓的误差放大、有色噪声等原因都将使最小二乘的法方程具有较强的病态性,需要采用正则化技术来稳定求解过程,本文采用Kaula正则化方法。形成法方程系数阵时采用时域滤波策略,分别采用PCCG方法和直接求逆法求解,经比较求解结果,发现在观测值包含误差的情况下,两种方法解算的结果几乎一致,这进一步表明PCCG方法求解法方程过程的快速有效性。限于篇幅,本文未给出SA方法的数学模型及解算方法,其具体实现及模拟计算结果可参阅文献[17]。本文所用观测值联合求解的方法是通过法方程矩阵加权叠加实现的,即每一类观测值单独形成法方程矩阵,最后进行法方程叠加。
从图中可看出,采用加权策略(使用AR滤波实现),可大大改善求解结果的精度,在整个频谱范围内均有很大提高,这也说明卫星重力梯度观测值中大的低频误差不仅影响重力场求解的低频部分。采用空域最小二乘方法求解的结果优于SA方法的结果,位系数精度在20到120阶的范围有明显提高,显示出空域最小二乘法求解过程的严密性。为了进一步比较求解模型的精度,表3给出了两种方法求解模型的大地水准面和重力异常误差统计结果。从表中可看出,不论是全球还是局部范围内,空域最小二乘法求解模型的精度均优于SA方法,尤其是全球的统计结果,这说明了空域最小二乘法较SA方法求解更稳定,受极空白区域的影响相对较小。虽然空域最小二乘法求解模型的精度较SA方法有提高,但并没有量级上的差异,大地水准面在±80°范围内均为几个厘米,重力异常的精度在1mGal以内,基本达到GOCE任务的目标要求。

图5 由空域最小二乘法和SA方法求解模型的阶误差均方差Fig.5 Degree error RMS of the gravity model estimated from space-wise LS method and SA approach

表3 由空域最小二乘法和SA方法求解模型的大地水准面和重力异常误差统计Tab.3 Statistics of geoid error and gravity anomaly error of the gravity model estimated from space-wise LS method and SA approach
此外,在本文模拟计算的情况下,空域最小二乘法以11个CPU同时计算大约需两周时间,同样的求解条件下,SA方法使用1个CPU仅需3h,所需内存也远小于空域最小二乘法,可见SA方法是一种快速有效的解算方法,但前面的分析比较是在观测值具有连续采样、近似重复等特性的基础上讨论的,若考虑数据有间断、非严格周期等情况,SA方法受到模型误差的影响会增大,此时可以预见空域最小二乘法相比SA方法应该有更好的稳定性。
4 结 论
本文研究了空域最小二乘法求解高阶GOCE卫星重力场的相关理论、方法与算法,提出基于AR模型对最小二乘过程中的有色噪声进行滤波处理,数值模拟结果说明了该方法的有效性。直接求逆法和PCCG法用于法方程求解的数值比较结果说明两者均能获得较高精度的解,PCCG效率更高,但无法提供完全的方差-协方差矩阵。基于含有误差(有色噪声和白噪声)的GOCE卫星任务模拟数据Vzz和SST,分别利用空域最小二乘法和SA方法分别恢复了180阶全球重力场模型,前者求解模型的精度优于后者,但SA方法所需的计算时间和资源都远小于空域最小二乘法。在未知实测数据真实特性的情况下,很难预见SA方法处理实测数据的性能,空域最小二乘法是一种可用于GOCE实测数据处理的稳定和较为严密的方法。需要指出,空域最小二乘法的快速解算问题需要作进一步研究,在当前拥有的计算机资源的条件下,若要对将来实测数据进行处理(更长周期、多种类型的引力梯度观测值,包括Vxx、Vyy等),研究并行算法在空域最小二乘解算(法方程形成、滤波、求逆以及正则化等运算)中的应用非常必要。
[1] ZOU Xiancai.Theory of Satellite Orbit and Earth Gravity Field Determination[D].Wuhan:Wuhan University,2007.(邹贤才.卫星轨道理论与地球重力场模型的确定[D].武汉:武汉大学,2007.)
[2] XU Xinyu,LI Jiancheng,ZOU Xiancai,et al.GOCE Gravity Explorer Mission[J].Journal of Geodesy and Geodynamics,2006,26(4):49-55.(徐新禹,李建成,邹贤才,等.GOCE卫星重力探测任务[J].大地测量与地球动力学,2006,26(4):49-55.)
[3] ESA.Gravity Field and Steady-state Ocean Circulation Mission:Report for Mission Selection,the Four Candidate Earth Explorer Missions[R].Noordwijk:ESA Publications Division,1999.
[4] RUMMEL R,VAN GELDEREN M,KOOP R,et al.Spherical Harmonic Analysis of Satellite Gradiometry[R].Delft:Netherlands Geodetic Commission,1993.
[5] KOOP R.Global Gravity Field Modeling Using Satellite Gravity Gradiometry[R].Delft:Netherlands Geodetic Commission,1993.
[6] LUO Zhicai.The Theory and Methodology of Determining the Earth’s Gravity Field Using Satellite Gravity Gradiometry Data[D].Wuhan:Wuhan Technical University of Surveying and Mapping,1996.(罗志才.利用卫星重力梯度数据确定地球重力场的理论和方法[D].武汉:武汉测绘科技大学,1996.)
[7] TSCHERNING C C.Computation of Spherical Harmonic Coefficients and Their Error Estimates Using Least Squares Collocation[J].Journal of Geodesy,2001,75(1):12-18.
[8] WENZEL H G.Geoid Computation by Least Squares Spectral Combination Using Integral Kernels[C]∥Proceedings of the International Association of Geodesy General Meeting.Tokyo:IAG,1982:438-453.
[9] KLEES R,KOOP R,VISSER P,et al.Efficient Gravity Field Recovery from GOCE Gravity Gradient Observations[J].Journal of Geodesy,2000,74(7-8):561-571.
[10] SCHUH W D,PAIL R,PLANK G.Assessment of Different Numerical Solution Strategies for Gravity Field Recovery[C]∥Proceedings of the“International GOCE User Workshop”.Noordwijk:ESA Publications Division,2001:87-95.
[11] SNEEUW N J.A Semi-analytical Approach to Gravity Field Analysis from Satellite Observations[D].Munich: Institute of Astronomy and Physical Geodesy,Technical University of Munich,2000.
[12] PAIL R,PLANK G.Assessment of Three Numerical Solution Strategies for Gravity Field Recovery from GOCE Satellite Gravity Gradiometry Implemented on a Parallel Platform[J].Journal of Geodesy,2002,76(8):462-474.
[13] PAIL R,PLANK G.GOCE Gravity Field Processing Strategy[J].Studia Geophysica et Geodaetica,2004,48(2):289-309.
[14] RUMMEL R,GRUBER T,KOOP R.High Level Processing Facility for GOCE:Products and Processing Strategy[C]∥Proceedings of the Second International GOCE User Workshop,"GOCE,The Geoid and Oceanography".Frascati:ESA-ESRIN,2004.
[15] XU Xinyu,LI Jiancheng,WANG Zhengtao,et al.The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission[J].Acta Geodaetica et Cartographica Sinica,2010,39(4):465-470.(徐新禹,李建成,王正涛,等.Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J].测绘学报,2010,39(4):465-470.)
[16] XU Xinyu,WANG Zhengtao,ZOU Xiancai,et al.The Research on Analysis and Simulation of Satellite Gravity Gradiometry Error of GOCE[J].Journal of Geodesy and Geodynamics,2010,30(2):71-75.(徐新禹,王正涛,邹贤才,等.GOCE卫星重力梯度测量误差分析及其模拟研究[J].大地测量与地球动力学,2010,30(2):71-75.)
[17] XU Xinyu,LI Jiancheng,JIANG Weiping,et al.The Fast Analysis of GOCE Gravity Field[C]∥International Association of Geodesy Symposia:Observing Our Changing Earth.Berlin:Springer,2009,133:379-385.
Simulation Study for Recovering GOCE Satellite Gravity Model Based on Space-wise LS Method
XU Xinyu1,2,LI Jiancheng1,2,JIANG Weiping1,2,ZOU Xiancai1,2
1.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;2.Key Laboratory of Geospace Environment and Geodesy Ministry of Education,Wuhan University,Wuhan 430079,China
The approach to deal with the colored noise in space-wise LS is discussed.The autoregressive(AR)filter is proposed to process the colored noise in the GOCE satellite gravity gradiometry,which is validated by the numerical results.The preconditioned conjugate gradient(PCCG)method and the direct inverse for solving the large normal equation are also verified by the numerical analysis.And the former approach is much faster than the latter one.Combing the radial component Vzzof the simulated gravity gradient tensor with colored noise and SST observation with white noise,the global gravity field model up to degree and order 180 is estimated by the spacewise LS method and the semi-analytical(SA)approach respectively.The accuracies of geoid and gravity anomaly of the global gravity field model estimated from the space-wise LS method are 3.01 cm and 0.75 mGal(1 Gal=10-2m/s2)respectively,which are better than them from the SA approach.
GOCE satellite;space-wise LS method;preconditioned conjugate gradient(PCCG);semi-analytical(SA);satellite gravity gradiometry;autoregressive(AR)model
XU Xinyu(1978-),male,PhD,lecturer,majors in satellite geodesy.
1001-1595(2011)06-0697-06
P223
A
国家自然科学基金(40904003;40804004;40637034);武汉大学自主科研项目(4082011)
雷秀丽)
2010-12-06
2011-02-23
徐新禹(1978-),男,博士,讲师,主要研究方向为卫星大地测量。
E-mail:xyxu@sgg.whu.edu.cn
