垂钻系统单轴稳定平台测量算法

孙 峰，王瑞和

(1.中国石油大学石油工程学院，山东青岛266555;2.中石化胜利石油管理局钻井工艺研究院，山东东营257017)

垂钻系统单轴稳定平台测量算法

孙 峰1，2，王瑞和1

(1.中国石油大学石油工程学院，山东青岛266555;2.中石化胜利石油管理局钻井工艺研究院，山东东营257017)

针对自动垂直钻井系统中采用的单轴稳定平台，在满足小井斜动态旋转条件下，提出一种新的以三轴加速度计和三轴磁通门测量信号为数据源的井斜方位动态测量算法，并考虑不同倾斜角和钻铤转速等因素的影响，对算法进行仿真研究。结果表明:小角度倾斜的方位角动态测量精度受倾斜角和真实方位角影响，在方位角相同的情况下，倾斜角越大，测量结果的误差越大，而在倾斜角相同的情况下，方位角为90°和270°时测量误差最大，且测量误差曲线随方位角变化呈现正弦变化的特点;经过误差函数补偿后的计算结果与真实值之间的误差曲线基本不受倾斜角、方位角影响，计算精度得到显著提高。理论计算与数值仿真结果均表明该算法有效可行，能够满足自动垂直钻井系统单轴稳定平台井斜方位角动态测量的精度需求。

垂钻系统;单轴稳定平台;小井斜;动态测量;数值仿真

为了解决高陡构造以及大倾角地层的防斜打快难题，通过自动垂直钻井系统能够有效地实现钻进过程中的主动防斜纠斜，从而保证井斜方位等工程参数的实时测量精度，实现井斜的自动控制。目前应用于自动垂直钻井系统上的稳定平台主要有两种:一种为机械式稳定平台，通过力矩平衡系统和复杂机械结构实现空间上绝对静止或缓慢转动，其上搭载的传感器件及测量算法等同于随钻测量中的静态测量，例如Schlumberger公司的Power-V系统中的随动稳定平台［1-4］;另一种为单轴稳定平台，该平台与钻铤固联，具有相同的运动状态及空间姿态，同时受震动、旋转离心力以及复杂井下工况例如黏滑的影响，它需要建立一个数学解析平台，通过全新的动态测量算法及传感器件的合理配置来保证测量的精度，例如自动垂直钻井系统中的捷联式稳定平台［5-8］。相比较而言，后者具有结构简单、体积小、可靠性高以及便于实现冗余等优点，但是如何实现复杂扰动环境下的动态测量，保证井斜方位测量精度，是必须要考虑的问题。笔者在静态测量原理的基础上，提出垂直钻井过程中小井斜条件下单轴稳定平台的动态测量算法，并进行仿真分析。

1 静态测量原理

单轴稳定平台上搭载的惯性器件为3个重力加速度计和3个磁通门，均两两正交，且轴坐标系安装重合，构成了测量探管坐标系，具有较高的测量精度和可靠性。具体的测量原理［9-13］如下:地球上任一点处的重力G及磁场强度B均可以通过测量得到，并且通过该点的垂直方向可以确定地理坐标系XYZ(北西天)，同时设定该点测量井斜方位的探管坐标系为xyz，根据欧拉旋转变换定理，xyz坐标系可由相对于地理坐标系XYZ的有限次转动表示，如图1所示。令(x3y3z3)为xyz系，则可得

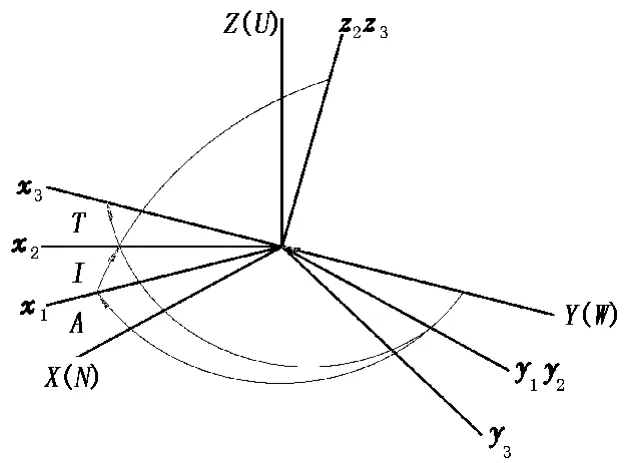
图1 欧拉旋转变换原理Fig.1 Principle of Euler rotation transformation

当A、I、T确定时，由图2三轴加速度计和三轴磁通门传感器安装示意图可得到重力信号G和地磁信号B在探管上的分量为

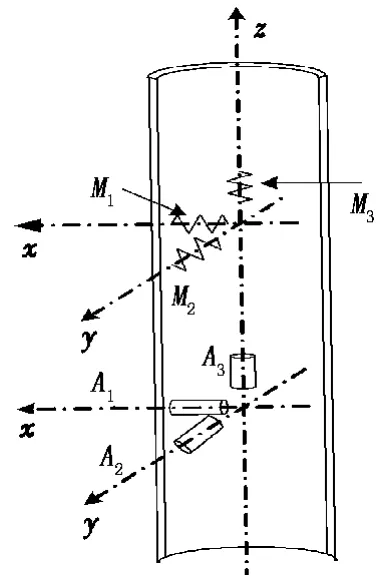
图2 三轴加速度计和三轴磁通门传感器安装示意图Fig.2 Installation sketch map of triaxial accelerators and magnetic fluxgate sensor

加速度计和磁通门可以测量探管上的重力分量和地磁分量，则工具面角、倾斜角、方位角及磁工具面角的计算公式分别为

倾斜角I=0时，测量值 Gx、Gy为0，不能由式(4)来计算工具面角T;当I很小时，Gx、Gy都很小，实际测量信号完全被噪声淹没，由重力分量所计算的工具面角T不准确，而磁分量Bx、By几乎不受倾斜角的影响。因此，工具面角由式(7)所计算的磁工具面角TB代替。当稳定平台处于静态或缓慢转动时测量原理按式(4)～(7)来进行计算。Sognnes等［14］在Bz轴信号受干扰不可用时，提出可利用地磁信号强度和磁倾角的先验知识及Bx、By信号反推真正的Bz信号，再进行方位角的计算。在实际应用中，为提高倾斜角、方位角及工具面角的计算精度，常以一段时间内重力分量和地磁信号分量的均值代入式(4)～(7)进行倾斜角、方位角的计算。

2 小井斜动态测量算法

在旋转状态下，重力分量G和地磁场强度B的测量分量随着转速呈周期性正弦变化，均值为零，静态测量方法不适用于旋转状态下井斜方位的测量。须建立新的动态测量方法来提高精度，实现准确测量。

垂直钻进过程中的动态测量属于小角度倾斜旋转时的动态测量，这时三轴加速度计和三轴磁通门可以简化为两轴，并且当倾斜角很小接近于零时，cos I≈1，sin I≈0，则代入式(3)可以得到近似方位角A的计算公式为

式(9)中第一项为sin A的直流成分，第二项和第三项均为工具面T的交流成分，故式(9)两端对工具面角T进行N个整周期积分后，仅剩余第一项(其中k=GBsin Icos Φ，Φ 为当地磁倾角)，即

式中，g为重力加速度。

式(7)、(12)和(13)构成单轴稳定平台在小井斜状态下动态旋转时的工具面角、方位角及倾斜角计算公式，需要注意的是式(12)和(13)的积分是关于磁工具面角的积分，而通常的数据采集是等时间间隔采样，所以要对加速度信号和磁通门信号进行等角度间隔重采样。

3 算法仿真及误差补偿

为了验证动态测量算法的合理性，建立仿真条件如下:假设当地重力加速度为g=10 m·s-2，地磁总强度B=4.84×10-5T，当地磁倾角Φ为45.5°，倾斜角 I为0.5°、1°、2°，方位角 A 从 1°变化到 350°，间隔1°，采样频率为100 Hz，探管旋转速度为0、60、120 r·min-1，依次间隔10 s，两轴加速度计的信噪比分别为1和10 dB，磁通门信号的信噪比为20 dB不变。图3为仿真用两轴加速度计信号和磁通门信号波形，其中倾斜角0.5°、方位角45°，加速度信号的信噪比为1 dB。

图3 加速度计和磁通门仿真信号Fig.3 Simulation signals of accelerators and flux-gate magnetometers

由式(14)可知，在倾斜角很小时，方位角A与磁性工具面角TB和重力工具面角T之间满足如下关系式:

由式(15)的推导过程可知，可以利用磁性工具面角和重力工具面角计算方位角，若记近似方位角A'与真实方位角A之间的差为ΔA，结合泰勒级数展开，可以证明

式(16)用于由式(12)所计算近似方位角的补

图4为不同信噪比、不同倾斜角I下的方位角计算误差曲线。由图4可以看出:对于所有倾斜角，方位角误差曲线均呈现明显的正弦特性，且仿真方位角在90°时误差达到正向最大值，270°时误差达到负向最大值;对于相同的方位角，倾斜角越大，方位角误差越大，表明倾斜角是该算法计算误差的最大影响因素，且最大误差正比于倾斜角。

为进一步提高方位角的测量精度，需进一步研究方位角与磁性工具面角和重力工具面角之间的关系。由式(7)可以得到偿，可进一步减小方位角测量值与真值之间的偏差。以图4(a)中倾斜角2°为例，算法补偿后的方位角计算误差曲线如图5所示。方位角误差最大值由补偿前的2.07°减小到补偿后的0.13°，从算法上保证了方位角测量的正确性。

图4 不同信噪比、不同倾斜角下的方位角计算误差曲线Fig.4 Azimuth computing errors at different deviation angles and different signal-to-noise ratio

图5 补偿前后方位角误差曲线对比(I=2°)Fig．5 Comparing of errors with and without compensation functions(I=2°)

4 结论

(1)自动垂直钻井系统单轴稳定平台所采用的测量算法实质是小角度倾斜旋转体的动态测量问题。该算法以三轴加速度计和三轴磁通门测量信号为数据源，得出了小井斜及动态旋转状态下井斜方位角的计算公式。

(2)小角度倾斜方位角动态测量的精度受倾斜角和真实方位角影响。在方位角相同的情况下，倾斜角越大，测量结果的误差越大;在倾斜角相同的情况下，方位角为90°和270°时测量误差最大，且测量误差曲线随方位角变化呈现正弦变化的特点。

(3)经过误差函数补偿后的计算结果与真实值之间的误差曲线基本不受倾斜角、方位角影响，计算精度得到显著提高。

［1］OPPELT J，CHUR C，FELD D，et al.New concept for vertical drilling of boreholes［R］.SPE 21905，1991.

［2］LIGRONE A，OPPELT J，CALDERONI A，et al.The fastest way to the bottom:straighthole drilling device drilling concept，design considerations，and filed experience［R］.SPE 36826，1996.

［3］MATTHIAS R，MARCUS O，HERMILO M，et al.Straight down to success:performance review of a vertical drilling system［R］.SPE 84451，2003.

［4］BRUSCO G，LEWIS P，WILLIAMS M.Drilling straight down［J］.Oilfield Review，2004，16(3):14-17.

［5］苏义脑，李松林，葛云华，等.自动垂直钻井工具的设计及自动控制方法［J］.石油学报，2001，22(4):87-90.

SU Yi-nao，LI Song-lin，GE Yun-hua，et al.The design and control ways of the downhole automatic colosed loop of vertical drilling tool［J］.Acta Petrolei Sinica，2001，22(4):87-90.

［6］韩来聚，倪红坚，赵金海，等.机械式自动垂直钻井工具的研制［J］. 石油学报，2008，29(5):766-768.

HAN Lai-ju，NI Hong-jian，ZHAO Jin-hai，et al.Development of mechanical tool for automatic vertical drilling［J］.Acta Petrolei Sinica，2008，29(5):766-768.

［7］王锡洲.捷联式自动垂直钻井系统的研制及现场试验［J］. 石油钻探技术，2010，38(3):13-16.

WANG Xi-zhou.Development and field test of automated strap-down vertical drilling system［J］.Petroleum Drilling Techniques，2010，38(3):13-16.

［8］孙峰，吕官云，马清明.捷联式自动垂直钻井系统［J］. 石油学报，2011，32(2):360-363.

SUN Feng，LÜ Guan-yun，MA Qing-ming.A strap-down automatic vertical drilling system［J］.Acta Petrolei Sinica，2011，32(2):360-363.

［9］吕妍红，万民，崔中兴.石油钻井倾斜及方位测量的研究［J］.仪器仪表学报，2002，23(2):131-133.

LÜ Yan-hong，WAN Min，CUI Zhong-xing.The research of oil drilling angle test［J］.Chinese Journal of Scientific Instrument，2002，23(2):131-133.

［10］XU T，LUO W S，LU H B，et al.Design of underground sonde of a directional drilling locator system［J］.Sensors and Actuators A:Physical，2005，119(2):427-432.

［11］赵建辉，孔琪颖，李帆.捷联惯性连续测斜算法仿真［J］.北京航空航天大学学报，2006，32(11):1286-1289.

ZHAO Jian-hui，KONG Qi-ying，LI Fan.Simulation of a strapdown inertial continuous wellbore survey algorithm［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32(11):1286-1289.

［12］刘白雁，苏义脑，陈新元，等.自动垂直钻井中井斜动态测量理论与实验研究［J］.石油学报，2006，27(4):105-109.

LIU Bai-yan，SU Yi-nao，CHEN Xin-yuan，et al.Theoretical and experimental investigation on dynamic measurements of hole inclination in automatic vertical drilling process［J］.Acta Petrolei Sinica，2006，27(4):105-109.

［13］乐识非.陀螺罗盘定向测量中工具面角计算方法探讨［J］.西安石油学院学报:自然科学版，2001，16(4):68-71.

LE Shi-fei.Discussion on calculation of tool face angle in gyrocompass measuring angle ［J］.Journal of Xi'an Petroleum Institute(Natural Science Edition)，2001，16(4):68-71.

［14］SOGNNES R，SMITH B，MCEIHINNY G.Improving MWD survey accuracy in deviated wells by use of a new triaxial magnetic azimuth correction method［R］.SPE 23852，1993.

Measurement algorithm in single-axis stabilized platform of vertical drilling system

SUN Feng1，2，WANG Rui-he1

(1.College of Petroleum Engineering in China University of Petroleum，Qingdao 266555，China;2.Drilling Technology Research Institute，Shengli Oilfield Administrative Bureau，SINOPEC，Dongying 257017，China)

For the single-axis stabilized platform in automatic vertical drilling system，under small inclination angle and dynamical rotation conditions，a new inclination and azimuth dynamical measurement algorithm was proposed based on triple axis accelerator and magnetic fluxgate sensors.Considering the effect of different rotation speeds，inclination angles and other factors，the algorithm was studied by numerical simulation.The results indicate that the dynamical measurement accuracy of small inclination angle is responsive to inclination and true azimuth.At the same azimuth circumstances，measurement errors increase with the increase of the inclination angle.In case of equal inclination，the curves of measurement errors are sinusoid approximately and the error would be the maximum as the azimuth of 90°or 270°.The errors between the real results and the compensation results by error function are little affected by inclination and azimuth，and the computing accuracy is improved significantly.The theoretical calculation and simulation results show the efficient of this algorithm，which can meet the requirements of dynamical measurement accuracy of small inclination of single-axis stabilized platform in automatic vertical drilling system.

vertical drilling system;single-axis stabilized platform;small inclination;dynamical measurement;numerical simulation

TE 243

A >

10.3969/j.issn.1673-5005.2011.03.015

1673-5005(2011)04-0085-04

2011-04-02

国家“863”高技术研究发展计划项目(2009AA093501);中国石油化工集团公司重大科技攻关项目(JP05011)

孙峰(1975-)，男(汉族)，山东邹平人，工程师，博士，主要从事钻井工程井下工具及仪器的科研工作。

(编辑 李志芬)