低比转速离心泵叶轮的水力设计数值方法

周 鑫，张永学，姬忠礼，江翠伟

(中国石油大学机械与储运工程学院，北京 102249)

低比转速离心泵叶轮的水力设计数值方法

周 鑫，张永学，姬忠礼，江翠伟

(中国石油大学机械与储运工程学院，北京 102249)

低比转速离心泵叶轮因扬程高、流量小、流道长而使内流状态复杂，其水力设计普遍采用基于相似理论的方法，叶轮水力性能高度依赖叶轮模型和设计者的经验。综合考虑相似理论设计经验成熟和叶轮空间流动理论设计的优势，采用二元流动理论，应用准正交线法绘制轴面流网，结合欧拉能量方程，进行轴面速度的迭代计算，根据轴面速度的分布要求，不断优化轴面流道轮廓，用贝塞尔曲线对叶片头尾部进行修圆，依据该方法编制的程序完成比转速为67的叶轮水力设计。结果表明:通过对相关参数的调整可实现低比转速离心泵叶轮的快速设计，设计所得叶片表面数据齐全，便于数控机床加工制造，还可结合各种优化程序对叶轮进行优化设计。

低比转速;离心泵叶轮;二元理论;轴面轮廓;贝塞尔曲线;设计

低比转速离心泵叶轮因其扬程较高、流量较小、流道狭长且曲率大，叶轮流道扩散严重，叶轮进口更易产生回流，出口更易发生脱流，导致出口附近的湍流结构相当复杂［1］，不易提高效率，因此对其进行好的水力设计比较困难。离心泵叶轮的水力设计已有很多方法，袁寿其等［2］对泵类流体机械的现代设计理论及方法作了总结，毕尚书等［3］对低比转速离心泵叶轮现有的水力设计新方法作了较全面的论述，杨军虎［4］提出了加大叶轮相关参数的设计方法，齐学义等［5］使用正交实验的方法对低比转速复合叶轮进行设计，王乐勤等［6-7］采用基于加大流量法对低比转速离心泵进行设计，杨军虎等［8］基于面积比原理对低比转速离心泵进行设计，王洋等［9］提出了采用加大流量法和堵塞流道法相结合的无过载离心泵设计方法。从这些研究可以看出，低比转速叶轮的水力设计当前仍然以基于相似理论的换算设计和速度系数法设计为主，设计出的叶轮水力性能很大程度上依赖于设计者的经验，且设计过程繁琐，没有采纳更加先进的水力流动理论。为此，笔者综合考虑相似理论设计经验成熟和叶轮空间流动理论先进的优势，自编全部数值计算程序，采用准正交线法计算轴面流网，用逐点积分法计算叶片骨线，用四点贝塞尔曲线对叶片头尾部进行修圆，结合欧拉能量方程确定的叶轮进出口环量要求，不断调整相关参数，实现低比转速离心泵叶轮的全数值水力设计。

1 水力设计数值方法

离心泵叶轮水力设计流程如图1所示:通过给定的设计参数依据速度系数法，获取基本尺寸参数，应用程序自动完成轴面流道轮廓的绘制;采用准正交线法，基于二元流动理论对轴面流网进行计算;在已获取的正交轴面流网的基础上，计算过流断面面积沿轴面流线的分布，并检验其分布是否合理，若过流断面分布不合理则对轴面流道进行修整并重新计算，直到过流断面面积分布情况满意为止;基于正交轴面流网，使用逐点积分法求取叶片轴面截线，以实现叶片骨线的绘形;在轴面上对叶片骨线进行加厚处理，采用贝塞尔曲线对其头部和尾部进行修圆，并检验叶片的光滑性。

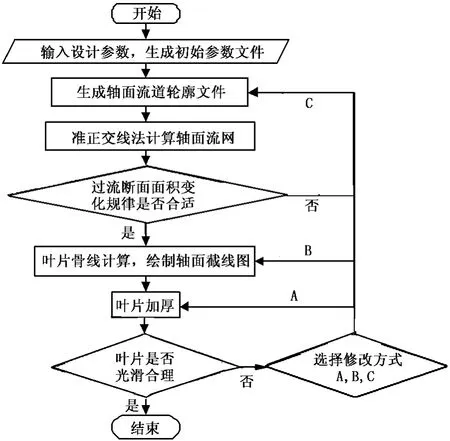
图1 程序流程图Fig.1 Program flow chart

1.1 轴面流道轮廓的确定

低比转速离心泵的轴面流道长且窄、曲率大，为便于叶轮的快速设计及相关参数的修改，在进行初始轴面流道设计时，前后盖板轮廓线选取直线及过渡圆弧，叶片的进口边形状采用直线型，进口边轮廓与轴线夹角 θ2依情况在30°～40°内选取(θ2选取过大会使进口边与轴毂连接处的叶片角过大，选取过小会产生流量扬程特性曲线不稳定问题)，轴面轮廓示意图见图2。叶片出口边使用与轴线平行的直线。为便于采用程序自动生成轴面流道轮廓线，利用离心泵速度系数法，确定流道的基本参数［10］。

图2 轴面轮廓示意图Fig.2 Schematic diagram of meridional profile

1.2 轴面流动计算

轴面流动采用准正交线法迭代计算，基本方程为轴面速度梯度方程，根据各子流道之间流量相等的原则进行迭代计算［11］，式中各量及坐标选取如图3所示。

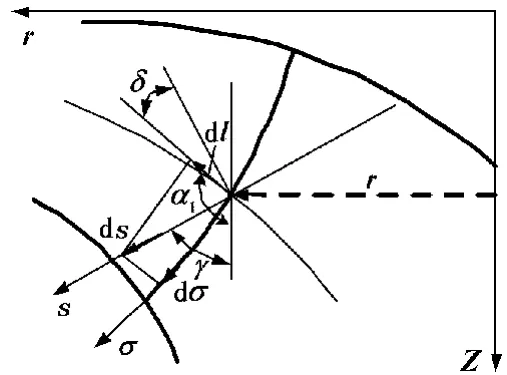
图3 准正交线、轴面流线及过水断面线之间的关系Fig.3 Relation of quasi-orthogonal lines，streamline and cross section line

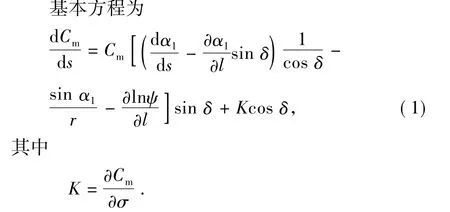
式中，Cm为轴面速度，m/s;s为准正交线长度，m;α1为轴面流线与铅垂线的夹角，(°);l为轴面流线长度，m;δ为准正交线的法线与流线之间的夹角，(°);

r为半径，m;ψ为排挤系数;K反映了轴面速度Cm沿着过流断面的分布情况。

式中，sc、sb分别为后、前盖板处准正交线长度。

1.3 过流断面检查及轴面流道轮廓调整

根据过流断面线与轴面流线正交的特性，只要轴面流线的形状确定，过流断面线的形状也就确定。在准正交线与轴面流线形成的轴面流网确定后，轴面流线在各个网格点上的斜率都可计算得到，根据这些初始数据，轴面流线上任意一点的斜率都可以通过插值方法进行计算，由此可确定经过该点的过流断面线在该点的斜率。对轴面流道轮廓进行调整时，首先作初始过流断面线，并调整过流断面线与轴面流线的交点位置，直至满足正交关系为止，由此确定过流断面线的形状及位置。然后计算过流断面沿轴面流线的分布情况，并与所需过流断面分布规律比较，若不满足则调整前后盖板轮廓上相应点的位置，重新计算直至满足要求。调整方法如下:假定所需过流断面分布函数为S=f(l)，计算所得过流断面面积为S'，过流断面线与初始轴面轮廓线交点p0坐标为(r0，Z0)。为获取所需轮廓线，沿该点处过流断面切线方向将 p0点移动到 p1(r1，Z1)，如图4(a)所示。当p0与p1相距较小时，可近似认为p1点为调整后的过流断面线与轴面轮廓线的交点，建立点p1的坐标与面积差值ΔS=S－S'的关系，求出调整后的轮廓线上点p1的坐标，从而实现对轴面轮廓的调整。

当后盖板形状不变，若取过流断面面积分布为线性变化，则前盖板轮廓调整前后如图4(b)所示，粗实线为调整后的前盖板轮廓线，其他细线分别为初始给定的前盖板轮廓线。由此可以看出，基于此方法，对于不同的前盖板轮廓，在相同过流断面变化规律下，最终都能将前盖板轮廓线调整到相同形状。

图4 轮廓调整示意图Fig.4 Sketch map of meridional profile adjustment

1.4 叶片绘形

假设叶轮由无限薄的无穷多叶片组成，则叶型骨线应与流线一致。在轴面流动计算中已经确定了轴面流线，再使用逐点积分法建立叶片包角φ与轴面流线长度l之间的关系，得到叶型的骨线积分方程为

通过轴面流网的计算，沿各轴面流线的r、Cm均已知，只要给出相对速度W沿轴面流线的分布规律，即可通过式(2)求得各点处的包角，经插值得到叶片轴面截线。相对速度W与水力损失及汽蚀性能有密切关系，从叶片进口到出口的相对速度可选用三次多项式表示为

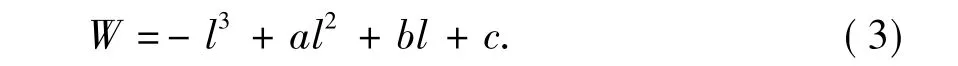
式中，l为轴面流线长。

在确定叶片进出口安放角后，进出口的相对速度W1、W2即可确定，再结合W先减速快，后减速慢的原则［12］(叶片进口处W快速减小可使压力迅速提高，以提高叶轮的抗气蚀性能，还能使边界层动量厚度增长尽可能小)，给定三次曲线上第三个点Wx以确定该曲线。

进行骨线方程积分时，通常给定包角，可通过不断修整参数m、n，逐次逼近直到计算所得包角与给定包角之差在允许误差范围内。

1.5 叶片加厚及叶片头部、尾部修圆

在获得轴面截线后在轴面上进行加厚的计算更简便、快捷。为减小误差，选择使用轴面流线方向的厚度进行计算。轴面流线方向的厚度为

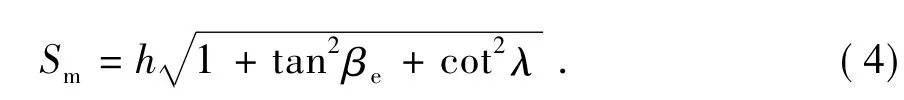
式中，h为计算点处叶片的真实厚度;βe为计算点处叶片的安放角;λ为计算点处轴面流线与轴面截线夹角。

在完成叶片绘形后，通过相关计算可获得叶片安放角βe及轴面流线与轴面截线夹角λ，再给定叶片真实厚度h沿轴面流线分布规律，可求出相应计算点处轴面流线长，即可完成叶片的加厚。

叶片的头部形状设置不合理会影响叶轮的汽蚀性能，尾部形状不合理会影响叶轮的流动分离及尾部涡脱落，造成流动损失增加，水力稳定性下降。现有方法大多采用在保角变换平面内进行修圆或在流面上修圆，这些方法只能实现头部及尾部的光滑处理，不能根据不同需求改变其形状。为此，本文中采用空间贝塞尔曲线对叶片头部和尾部进行光滑处理，叶片的压力侧及吸力侧使用四点Bezier曲线，如图5所示(图中点为贝塞尔曲线控制点)，通过对控制点的修改实现对叶片头部、尾部形状的控制。Bezier曲线方程［13］为

图5 叶片头部修圆示意图Fig.5 Schematic diagram of leading edge of blade rounding

2 叶轮水力设计

叶轮水力设计参数:流量Q=45.68 m3/h，扬程H=46.41 m，转速n=2900 r/min。根据速度系数法［10］，叶轮基本参数:进口直径Dj=66 mm，轮毂直径dh=0，出口宽度b2=9 mm，外径D2=202 mm，叶片数Z=5。

使用相关程序生成初始轴面流道轮廓，如图6所示。

图6 轴面流道轮廓Fig.6 Meridional profile

调用轴面流网计算程序，选好k值进行轴面流动计算，待计算完成后检验过流断面面积沿轴面流线分布(图7)。从图7可看出，初始的轴面轮廓不满足要求，使用轮廓调整程序，按所选过流断面面积沿轴面流线线性变化的规律对轴面流道轮廓进行调整，直到满足要求。调整后计算所得过流断面线、轴面速度矢量图和轴面速度分布分别见图8、9。

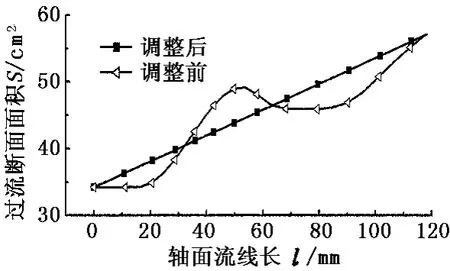
图7 过流断面面积沿轴面流线分布Fig.7 Distribution of cross section area along meridional streamline

图8 过流断面线和轴面速度矢量图Fig.8 Cross section lines and meridional velocity vectors

k值反映轴面速度分布情况，其值的选取对叶轮设计有很大影响。由图9可见，当取k≠0时，轴面速度的不均匀程度及其范围明显增大，且这种变化随着k值的增大而增大。在二元理论设计中，轴面速度分布规律从后盖板到前盖板的各条流线上都有明显差异，后盖板轴面速度沿轴面流线变化规律为先减小后增大再减小，前盖板基于轴面速度沿轴面流线为先增大后减小。再者，基于一元理论设计的叶片其轴面速度最小值出现在出口附近，而基于二元理论设计的叶片其最小速度出现于后盖板附近。对离心泵叶轮来说，由于叶片进口处的水流冲击会在后盖板处形成高压，从而会使得该处速度有最小值。由此说明基于二元理论的设计较一元理论的传统设计更能反映真实流动。

图9 轴面速度分布Fig.9 Distribution of meridional velocity

图10为k取不同值时轴面流线的分布。从图10可以看出，随着k逐渐增大，轴面流线逐渐远离叶轮后盖板，也即随着k逐渐增大，轴面流线弯曲部分的曲率逐渐减小。流线的曲率影响叶轮流道内的流动边界层，进而影响叶轮内流动的稳定性。

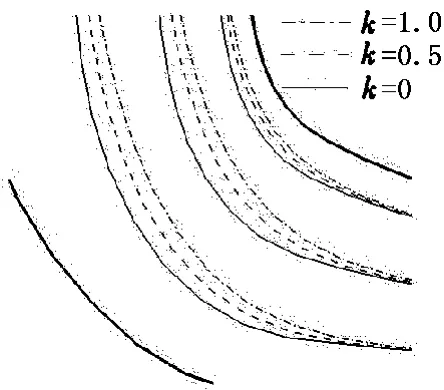
图10 不同k值对轴面流线的影响Fig.10 Effect of different k on streamline

待轴面流动计算完成后，使用骨线计算程序对叶片进行绘形。叶片进口处的相对速度值由进口环量(对于法向进口，取0)、进口轴面速度及进口叶片安放角计算，叶片出口处的相对速度由根据欧拉能量方程计算出的叶片出口环量、出口轴面速度及出口叶片安放角计算，再应用前面给出的轴面相对速度分布函数(图11)，使用逐点积分法完成叶片的绘形。图12为叶片轴面截线局部放大图。

图11 相对速度沿流线分布Fig.11 Distribution of relative velocity along streamline

轴面截线计算完成后，调用加厚及头部修整程序进行计算。叶片厚度分布规律为:最大厚度选在叶片全长的1/3处，其估算公式选用为厚度系数)，为减小阻塞，在满足铸造要求的前提下尽可能减小进口部分厚度，故选为3 mm，对于低比转速叶轮而言，流道扩散严重，适当地增大排挤系数有利于提高扬程，故叶片出口部分厚度使用叶片最大厚度。在轴面上对叶片进行加厚计算，使用本文中所述的四点空间Bezier曲线对叶片头部和尾部进行修整，叶片头部修整图见图13(a)。将计算后的相关数据导入三维建模软件，生成模型见图13(b)。

图12 轴面截线图Fig.12 Meridional shape of impeller

图13 叶片头部修圆和叶轮模型图(移除前盖板)Fig.13 Leading edge of blade rounding and impeller model with shroud removed

应用有限体积法及RNG k－ε湍流模型［14］对文中所给设计参数分别基于传统一元理论设计及二元理论设计的叶轮进行模型分析，并计算相应设计工况下的水力效率。结果表明，基于二元理论所设计的叶轮水力效率与一元理论所设计叶轮相比有一定的提高。

3 结束语

针对传统离心叶轮设计方法的繁琐及不足，提出了结合准正交线法、逐点积分法的二元理论低比转速离心叶轮数值水力设计方法，并在此基础上提出了基于过流断面面积变化规律自动进行调整轴面轮廓的方法。依据该方法编制的程序，通过对相关参数的调整可实现低比转速离心泵叶轮的快速设计，设计所得叶片表面数据齐全，便于后续正问题计算以对设计叶轮的水力性能进行预测，也便于数控机床加工制造，该方法还可结合各种优化程序对叶轮进行优化设计。

［1］彭晓强，张永学，曹树良，等.低比转数离心泵叶轮出口紊流流动结构分析［J］.农业机械学报，2004，35(1):69-72.

PENG Xiao-qiang，ZHANG Yong-xue，CAO Shu-liang，et al.Numerical-analysis of 3D turbulent flow in a low specific speed pump impeller［J］.Transactions of the Chinese Society of Agricultural Machinery，2004，35(1):69-72.

［2］袁寿其，刘厚林.泵类流体机械研究进展与展望［J］.排灌机械，2007，25(6):46-51.

YUAN Shou-qi，LIU Hou-lin.Research progress and prospect on fluid machinery-pumps［J］.Drainage and Irrigation Machinery，2007，25(6):46-51.

［3］毕尚书，王文新，严敬，等.低比转速离心泵叶轮水力设计新方法综述［J］.机械，2008，35(10):4-7.

BI Shang-shu，WANG Wen-xin，YAN Jing，et al.Summarize of the new methods for low specific-speed centrifugal impellers'hydraulic design［J］.Machinery，2008，35(10):4-7.

［4］杨军虎.低比转数离心泵叶轮内的流动机理和叶轮设计［J］.农业机械学报，2002，33(2):47-49.

YANG Jun-hu.Flow mechanism inside the impeller of a centrifugal pump with low specific speed and design of the impeller［J］.Transactions of the Chinese Society of Agricultural Machinery，2002，33(2):47-49.

［5］齐学义，胡家昕，田亚斌.超低比转速高速离心泵复合式叶轮的正交设计［J］.排灌机械，2009，27(5):341-346.

QI Xue-yi，HU Jia-xin，TIAN Ya-bin.Orthogonal design of complex impeller of centrifugal pump with super-lowspecific-speed［J］.Drainage and Irrigation Machinery，2009，27(5):341-346.

［6］王乐勤，朱祖超.低比转速低温高速离心泵复合叶轮的设计与工业应用［J］.低温工程，1998(3):32-37.

WANG Le-qin，ZHU Zu-chao.Design and industrial application study of complex impeller of low-specific-speed，low-temperature and high-speed pump［J］.Cryogenics，1998(3):32-37.

［7］倪永燕，袁寿其，袁建平，等.低比转速离心泵加大流量设计模型［J］.排灌机械，2008，26(1):21-24.

NI Yong-yan，YUAN Shou-qi，YUAN Jian-ping，et al.Model of enlarged flow design for low specific speed centrifugal pump［J］.Drainage and Irrigation Machinery，2008，26(1):21-24.

［8］杨军虎，张人会，王春龙，等.低比转速离心泵的面积比原理［J］.兰州理工大学学报，2006，32(5):53-55.

YANG Jun-hu，ZHANG Ren-hui，WANG Chun-long，et al.Area-ratio principle for centrifugal pumps with low specific-speed［J］.Journal of Lanzhou University of Technology，2006，32(5):53-55.

［9］王洋，何文俊.基于Fluent的无过载离心泵改型设计［J］.农业机械学报，2009，40(9):85-88.

WANG Yang，HE Wen-jun.Improved attempt of non-overload centrifugal pumps based on fluent［J］.Transactions of the Chinese Society of Agricultural Machinery，2009，40(9):85-88.

［10］GÜICH J F.Centrifugal pumps［M］.Heidelberg:Springer Berlin Heidelberg，2008:348-350.

［11］曹树良，梁莉，祝宝山，等.高比转速混流泵叶轮设计方法［J］.江苏大学学报:自然科学版，2005，26(3):185-188.

CAO Shu-liang，LIANG Li，ZHU Bao-shan，et al.Design method for impeller of high specific speed mixedflow pump［J］.Journal of Jiangsu University(Natural Science Edition)，2005，26(3):185-188.

［12］沈天耀.离心叶轮的内流理论基础［M］.杭州:浙江大学出版社，1986:273-275.

［13］DONALD Hearn，PAULINE Mo Baker.Computer graphics coversion［M］.2nd ed.London:Prentice Hall，1996:327-333.

［14］张金亚，朱宏武，李艳，等.基于正交设计方法的混输泵叶轮优化设计［J］.中国石油大学学报:自然科学版，2009，33(6):105-110.

ZHANG Jin-ya，ZHU Hong-wu，LI Yan，et al.Optimization design of multiphase pump impeller based on orthogonal design method［J］.Journal of China University of Petroleum(Edition of Natural Science)，2009，33(6):105-110.

Hydraulic design of low specific speed centrifugal pump impeller by numerical method

ZHOU Xin，ZHANG Yong-xue，JI Zhong-li，JIANG Cui-wei

(Faculty of Mechanical and Oil-Gas Storage and Transportation Engineering in China University of Petroleum，Beijing 102249，China)

Considering the complexity of the flow state with high head，low capacity and long passage，the hydraulic design of low specific speed centrifugal pump impellers was based on similarity theory and its hydraulic performance is highly dependent on the model of impeller and experience of designer.A numerical method was put forward combining the advantages of similarity theory design and 2D theory design，adopting quasi-orthogonal method and Euler energy equation to calculate meridional velocity distribution，adjusting the meridional profile according to the cross section area，drawing blade shape by point-by-point integration method，thickening blade and smoothing leading edge of blade by using Bezier curve.The design of the impeller(specific speed of 67)was completed.The results show that the low specific speed centrifugal pump impeller design can be achieved through the adjustment of parameters，and the design data from the blade surface is complete.It is easy to process and manufacture the numerical control machine tools.The design of the impeller can be optimized using various optimization program.

low specific speed;centrifugal pump impeller;2D theory;meridional profile;Bezier curve;design

TH 311

A >

10.3969/j.issn.1673-5005.2011.04.021

1673-5005(2011)04-0113-06

2010-10-12

国家自然科学基金青年基金项目(50809075);北京市重点学科资助项目

周鑫(1986-)，男(汉族)，湖北黄石人，博士研究生，从事低比转速离心泵正反问题数值研究。

(编辑 沈玉英)