衡量收入分配差距的计量经济学方法——对均等指数法的疑问及改进

郭 平,彭妮娅,潘郭钦

(1.湖南大学经济与贸易学院,湖南长沙 410079; 2.湖南商学院会计学院,湖南长沙 410079)＊

衡量收入分配差距的计量经济学方法
——对均等指数法的疑问及改进

郭 平1,彭妮娅1,潘郭钦2

(1.湖南大学经济与贸易学院,湖南长沙 410079; 2.湖南商学院会计学院,湖南长沙 410079)＊

利用分组数据对均等指数的计算过程与理论前提不相符,导致了不同的分组情况会得出不同的均等指数,这降低了其度量收入差距的可信度。基于对均等指数的这一疑问以及均等指数的构建与均方差只相差与样本容量相关的常数倍这一现象,提出了衡量数据离散程度的方差可以衡量收入分配内部差距的原理,结合计量经济学中线性回归的判定系数和回归斜率,可以很好地衡量收入差距,并用实证分析证明了此方法的可行性。

收入差距;计量经济学;方差;实证

一、引 言

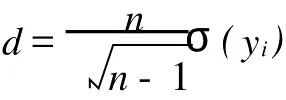
二、收入分配均等指数法简介与疑问

(一)收入分配均等指数的思想原理与构建

均等指数的构建是于等分法的基本思想,等分法的基本作法是:通过统计调查方式,将一定社会中的一定数量的居民(或家庭)按收入水平由低到高排序;在此基础上,将这些居民依次划分为不同的组,使每组有相同的居民(或家庭)数;计算出每个收入组的平均收入水平,这个平均收入水平即代表该收入组的收入水平;通过比较各收入组的平均收入水平,从而可以得到总体居民收入分配直观上的度量(见图1)。比如,五等分法是把一个社会中的居民按收入水平由低到高依次分为5个收入组,且每个收入组人数相同。如果收入平等地分配到所有居民之间,每组的居民都应该得到1/5的收入。这是收入绝对均等的情况。构建方法及性质详见李军和张丹萍的研究[1]。

图1 三种不同角度的收入比重比较

(二)对收入分配均等指数方法的疑问

均等指数方法的构造过程简单明了,且有完整严格的数学证明,似乎是度量收入差距的一个很好的指标,但数学上完整的证明不能代表实际操作中的准确无误。因为大多数人在理论的论证完整性面前忽视了理论前提与现实数据获得的差异,而出现了一些有待商榷的做法。

上述均等指数的构建原理是基于等分法,而指数公式的导出却是以样本个体为对象,这两者看似不矛盾,但实际上基于分组的数据与未分组的个体数据在计算中会使结果存在较大差异,即便同样都用分组数据,只是分组方式不同,计算结果也截然不同。数值结果的不唯一性使得按均等指数方法得出的结果缺乏可比性与可信度。

下面以一个简单具体的例子进行说明。假设有100个个体,收入分别为1,2,…100,采用均等指数法计算但有几种不同的分组情况,可能出现以下结果:

(1)计算对象为个体时,用各自收入除以总收入5050即得各自收入比重分别为 x1,x2,…x100,平均收入比重为0.01,取n=100,可得:

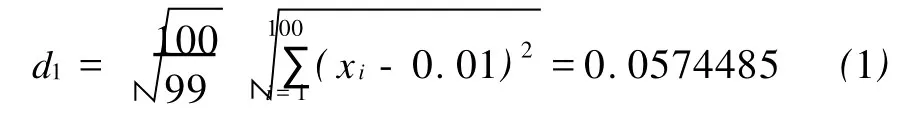
(2)若将个体进行分组,按收入由低到高分为10组,每组10人,则这10组的比重分别为:

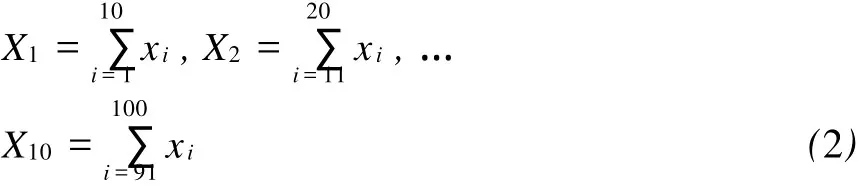
此时的平均比重为0.1,但是取n=10,计算得:

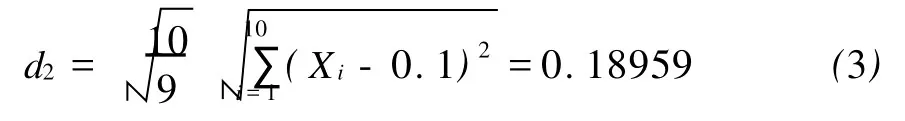
(3)若将个体按收入由低到高分为5组,每组20人,则这5组的比重分别为:

此时的平均比重为0.2,取n=5,计算得:

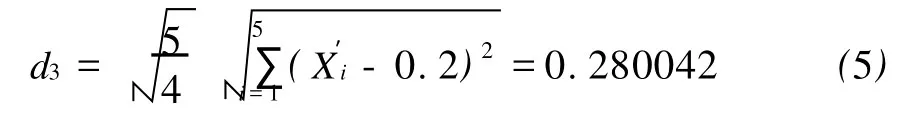
由此可见,同样的数据,只是分组的方法不同,导致算出来的结果相差近5倍,并且组数越少均等指数的数值越大,所以用均等指数衡量收入分配公平性的方法还需继续研究。

三、衡量收入分配差距的计量经济学方法

现从均等指数的构建出发,介绍计量经济学中的方差概念[3]与之的相似性及用方差衡量收入分配的方法。

(一)离散随机变量的期望与方差

从公式(6)～(8)可发现,数组的期望即为该数组的平均值,若相比收入分配比重即为平均比重,而方差表示的是数组离开平均值的离散程度,且有

而均方差即为方差的开方,亦可衡量数据与平均值的离散程度。

并且均方差和均等指数有如下关系:

由于方差的意义表示数组的离散性,便可以根据收入分配等分法,通过统计调查方式,将一定社会中的一定数量的居民(或家庭)按收入水平由低到高排序;在此基础上,将这些居民依次划分为不同的组,使每组有相同的居民(或家庭)数;计算出每个收入组的平均收入水平,这个平均收入水平即代表该收入组的收入水平;通过比较各收入组的平均收入水平,从而得到总体居民收入分配直观上的度量。

既然对于均等指数而言,不同的分组会有不同的数值结果,就要尽量避免分组的影响,下面的衡量收入差距的方法将从整体与内部两方面考虑,而避免分组造成结果不可信的影响。

(二)回归直线衡量整体差距与内部差距

当得到收入分配等分法描述的各收入组数据后(这也是通常情况能得到的数据,如统计年鉴),可以收入家庭比重为解释变量,以各组收入比重为被解释变量进行一元线性回归,然后根据回归直线的斜率和拟合优度判定收入差距的大小。

定理1 按收入等级分组,以收入组比重为解释变量,以各组收入比重为被解释变量的一元线性回归中,回归直线斜率大小与总体公平程度成反比。即斜率越小越公平,斜率越大越不公平。

证明:根据度量收入分配的等分法的定义易证。

如图2,两条曲线所代表的数据公平差距不同,从几何意义可直观地看出,收入差距较小的曲线拟合的直线斜率较小,而收入差距较大的曲线拟合直线的斜率较大。

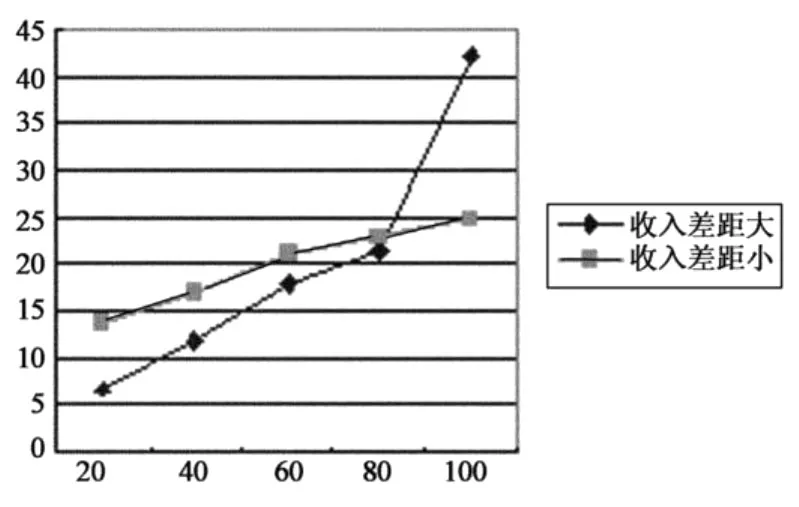
图2 公平程度不同的两组收入数据

定理2 据定理1所述拟合的回归直线的斜率值域为(0,+ ),当斜率为0时是绝对公平的情况,当斜率为+时则绝对不公平。

证明:根据度量收入分配的等分法的定义易证。

定理3 据定理1所述拟合的回归直线的判定系数与内部公平程度成正比,即判定系数越大越公平,判断系数越小越不公平。

证明:设一元线性总体回归模型[4]为:

两边取均值得总体回归方程:

设样本回归直线为:

样本回归直线是对样本数据的一种拟合,对与同一组样本数据,用不同的方法去估计回归直线的参数,可以拟合出不同的直线。从散布图上看,所有样本观测值都恰好在回归直线上的情况是极少见的,回归直线与样本观测值总是存在或正或负的偏离,样本回归直线与样本观测数据之间的拟合程度,称为样本回归线的拟合优度,在计量经济学中,拟合优度是用在总变差分解的基础上确定的样本判定系数去度量的。

为了说明样本判定系数的意义,考察被解释变量的总变差的组成情况。由于样本回归函数为:

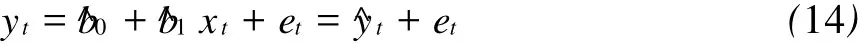
yt=+et可用离差形式表示:

对于全部观测值求平方和,有:

由于

图3 因变量离差的分解

所以有

这样式(21)～(23)可写为 :

上式两边同除以 TSS,得:

判定系数R2是回归直线对各观测点拟合紧密程度的测度。判定系数越大,各观测值在拟合直线附近越紧密,离散程度越小。

当观测值为度量收入分配的等分法的各收入组的收入比重时,收入分配越公平,各收入组间差距越小,观测值离拟合直线越近,即 R2越大。即判定系数的大小与组内公平性成正比。证毕。

据上文所述,以收入分配等分法的数据作线性回归,依据拟合直线的斜率与拟合优度即判定系数的大小综合判断收入分配的公平性,斜率大小表明整体差距,判定系数表明内部差距,斜率越小越公平,判定系数越大越公平。亦可看判定系数与拟合直线的斜率的差值,此差值越大,越公平。

四、实证研究及结论

下面用全国2000～2008年的城镇居民收入数据[5],如表1所列,计算出各收入等级的收入占累积总收入的比重。

下面以人口累积比重为解释变量,以各组收入比重为被解释变量进行一元线性回归,用Eviews软件操作结果如表2所示。

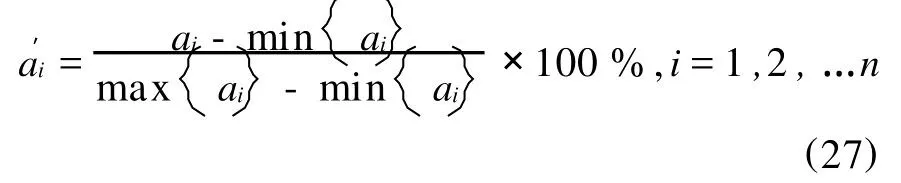
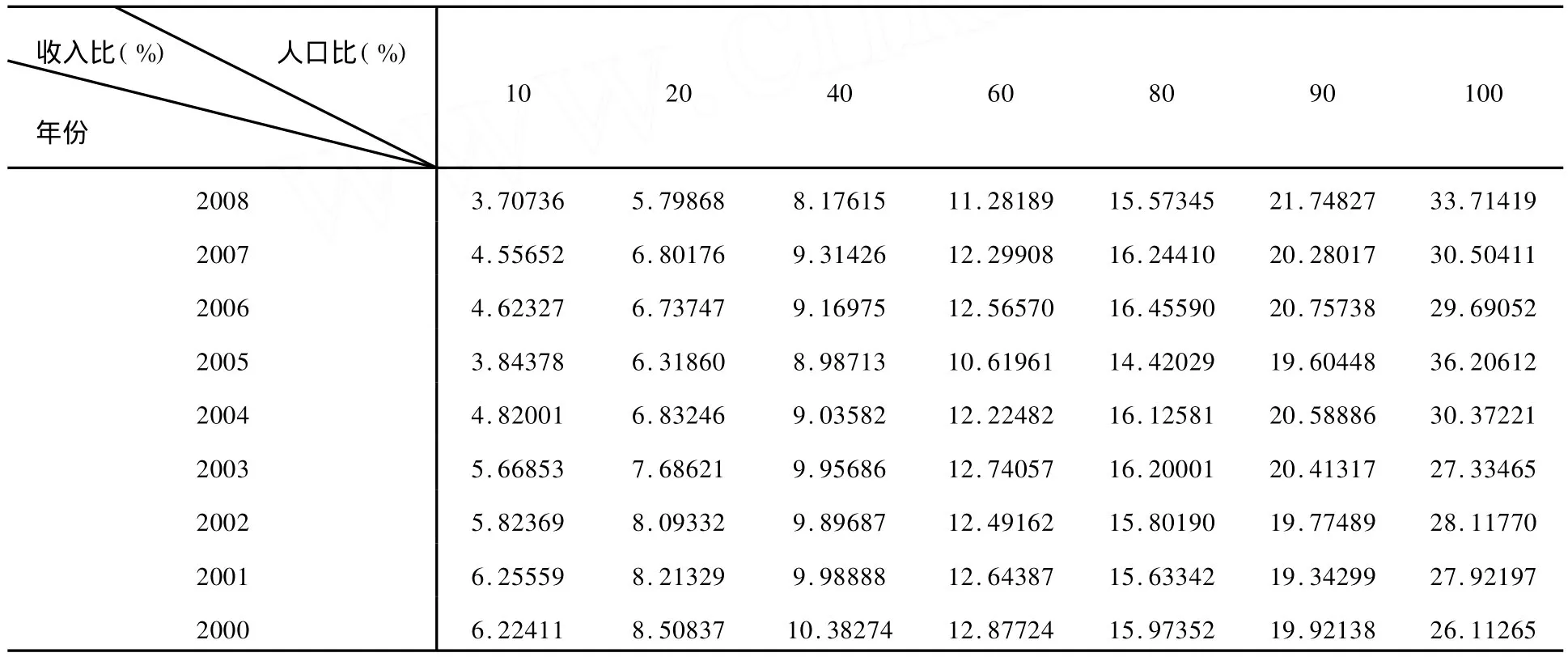
表1 按收入等级划分的各收入组各自收入比重

表2 回归直线斜率及判定系数

表3 回归直线斜率即判定系数调整后数据

表4 根据三种方法判断收入公平性的排名结果

根据此方法对各年收入分配公平性的比较与根据基尼系数方法[6]的有所不同,列表比较见表达方式。

以上所述方法既有理论依据,又有实证支持,这异于收入分配均等指数法。收入分配均等指数法理论上虽成立,但现实操作中难度大,易出错。根据回归直线斜率及判定系数的计量经济学方法操作简便,直观易懂,其结果可信性也通过实证加以证明,是对于衡量收入分配公平性的方法的较有力的补充和扩展。

[1]李军,张丹萍.度量收入分配的均等指数方法及其应用[J].数量经济技术经济研究,2005,(6):33-42.

[2]杨少华,彭维湘.对社会不公平程度的度量[J].统计与决策, 2006,(9):76-78.

[3]高铁梅.计量经济分析方法与建模——EViews应用及实例[M].北京:清华大学出版社,2006.

[4]孙敬水.计量经济学教程[M].北京:清华大学出版社,北京交通大学出版社,2005.

[5]中国统计年鉴编辑部.中国统计年鉴[M].北京:中国统计出版社,2009.

[6]郭平,彭妮娅.基于等基尼系数线的平均增长点方法研究[J].财经理论与实践,2009,(5):81-85.

An Econometrics Method of Measuring Disparity of Income Distribution: Question and Improvement of Equalization Index

GUO Ping1,PENG Ni-ya1,PAN Guo-qin2

(1.School of Economics&Trade,Hunan University,Changsha,Hunan 410079,China; 2.School of Accounting,Hunan University of Commerce,Changsha,Hunan 410079,China)

The paper discovered that the calculating of equalization index based on group data is not consistent with its theory premise.Eecause different grouping will lead to different result, the credibility of equalization index in measuring disparity of income distribution has been questioned.Based the fact that equalization index is a multiple of mean squared deviation and sample numbers.The paper advanced a new way of using variance to measure income disparity.Combined with adjusted R-square and regression slope in econometrics,variance can well explain the disparity of income.The paper has been proved the feasibility of the new way with empirical samples.

Disparity of Income;Econometrics;Variance;Empirical Study

F224 文献标识码: A 文章编号:1003-7217(2011)03-0094-05

2010-11-12

教育部新世纪优秀人才支持计划项目(教技函[2007]70号)

郭 平(1963—),男,湖南株洲人,湖南大学经济与贸易学院教授,博士生导师,研究方向:财税理论与国有资产管理;彭妮娅(1985—),女,湖南岳阳人,湖南大学经济与贸易学院博士研究生,研究方向:财税理论与计量经济学。

(责任编辑:王铁军)