一种新的基于部署知识的WSN密钥分配方案*

袁猷南，杨明慧，游 林(杭州电子科技大学通信与信息系统研究所，杭州310018)

无线传感器网络的安全通信中，节点密钥建立极其重要。由于WSN节点计算能力、能量和存储空间以及通信带宽受限等问题，使得传统的安全技术不能够很好的应用在无线传感器网络中。目前普遍采用密钥预分配技术进行密钥分配，即在传感器部署前由离线服务器将密钥或产生密钥的信息预先存储在节点中。

文献［1］中，Eschenauer和Gligor提出了基本的概率密钥分配方案，在此基础上出现了该方案的一系列改进［2－3］，文献［2］要求节点间至少有 q 个共同密钥才能建立对密钥，抗俘获能力有所改善，文献［3］利用哈希函数不可逆性提高了E－G方案的抗毁性。文献［4］提出了Blom方案，它具有安全门限等特点，只要被俘节点不超过这个安全阈值，则节点对捕获免疫。文献［5］把组合设计引入到无线传感器网络中，利用组合设计的不完全区组设计(Balanced Incomplete Block Design，BIBD)以及有限射影平面(FPP)构造节点密钥，优点是网络中任何两个节点之间能够直接建立对密钥，降低了通信负荷，缺点是抗毁性差。文献［6－10］提出了一种基于部署信息的密钥方案，利用节点部署时同一区域内节点成为邻居节点的概率高而不同区域内节点为邻居节点的概率小的特点，网络性能明显改善。

为了改善网络的本地连接概率和抗毁性能，本文在基于部署知识的基础上，利用Blom矩阵、t次多项式和哈希链，提出了一个新的适合无线传感器网络密钥分配方案——KD－DK。

1 背景介绍

1．1 节点部署模型

假设节点从高空投放后静止不动，同一批次投放的节点容易落在一个区域，将该区域称为Cell，则同一个Cell或相邻Cell的节点之间成为邻居节点的概率更高。设投放区域总面积为X×Y，X为长，Y为宽，将其划分为M×T个Cell。常用的Cell有矩形或是正六边形。设节点的发射半径为R，则矩形所覆盖面积为R2/8，正六边形覆盖面积可达3R2/26，约为矩形的1．598 8倍，因此本文采用正六边形。图1所示，每个Cell按＜i，j＞编号作为其 ID，其中1≤i≤M，1≤j≤T。设节点实际部署服从二维高斯分布，记节点 node∈Cell＜i，j＞为事件 A，则 A 的概率密度函数 f(A)满足式(1)，其中 ＜xi，yi＞为Cell＜i，j＞的实际部署坐标，＜ x，y ＞ 为 node的实际部署坐标，σ为节点部署的标准方差。

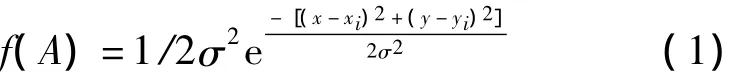
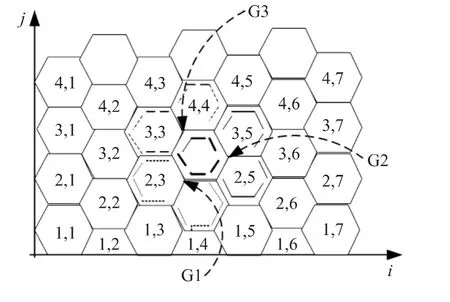
图1 节点的部署模型

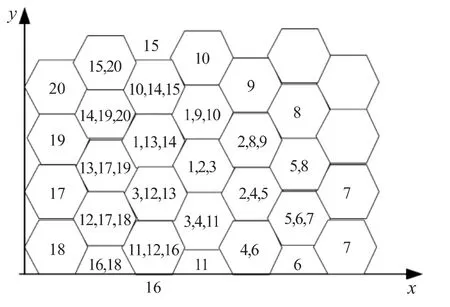
图2 网络密钥池的分配

1．2 Blom 矩阵

Blom矩阵利用素域GF(q)上形成的密钥对生成矩阵A×G来定义节点间的密钥对，其中q是能够支持网络节点数的最小的素数，G是一个(λ+1)×N的公共矩阵，N可认为是网络节点数目，λ为网络安全阈值，即只要网络中被俘的节点数不大于λ，就不会对现有节点构成威胁。G通常由范德蒙矩阵生成，因此每个节点只需存储每列的第二个元素就可以衍生出整个列，可以减少节点的存储空间。

令A=(D×G)T，D为一个保密的随机对称矩阵，D=(λ+1)×(λ+1)，则 A×G对应一个N×N的对称矩阵。若记Kmn为A×G中的第m行和第n列的值，则有:Kij=Kji。每个节点根据自己的编号i存储矩阵A的第i行和矩阵G的第i列。当节点i和j要生成共享密钥时，彼此交换自己所存储的G的列，然后根据矩阵乘法计算各自的Kij和Kji，由于Kij=Kji，这样节点i和j建立起了对密钥。

1．3 二元对称t多项式

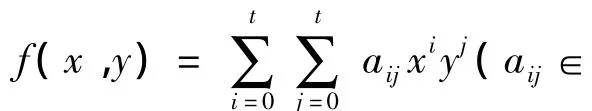
1．4 哈希链

定义2 (哈希链)给定一个种子Seed和哈希函数H(X)(如SHA-1或MD5)，按照下面过程构造一系列哈希值:Vn=H(Seed)，Vi=H(Vi+1)，n为哈希链长度，1≤i≤n。

2 密钥分配方案KD－DK

2．1 KD－DK密钥池的构造

网络部署之初，密钥分发服务器(Key Distribution Sever，KDS)需要为每个节点分配一些密钥信息，文中常用符号如表1所示。

为分析方便，考虑将邻近的6个Cell划分为3组:GP1、GP2和 GP3，如上图1所示。其中。KDS 产生 3 个子密钥池 S1、S2和 S3(互不重叠)分别分配给 GP1、GP2和 GP3，|Si|=SC，i=1，2，3。网络中的每个节点分别从相邻的三个组的密钥池中选出m/3个密钥，因此每个节点就保存了mR个密钥。这样网络中不同Cell的节点间总能找来自同一个子密钥池的元素。例如图1所示，GP1、GP2和GP3共同的分别从S1、S2和S3选出m/3个密钥。根据上述原理，可得图1所示的网络密钥池的配置如图2所示，其中节点中的数字表示密钥池的序号。可以看出任意两个相邻Cell必定拥有一个共同的密钥池。

表1 文中常用符号

2．2 KD－DK方案描述

KD－DK方案中，Cell内采用改进的Blom矩阵，Cell间采用改进的随机密钥方案以达到不同Cell间邻节点建立直接对密钥以保证良好的抗毁性。该方案基于以下假设前提:网络节点部署开始很短的一段时间Tmin内没有节点被敌方物理俘获。该方案包含三个阶段:①密钥预分配;②密钥对建立;③路径密钥建立。

2．2．1 密钥预分配

根据密钥池构造和密钥分配原理，网络中的每个节点预配置mR个密钥，同时存储同一个二元t次对称多项式f(x，y)产生的份额f(u，y)，u为中节点自身ID。

2．2．2 密钥对的建立

为保证节点安全通信，邻节点间必须建立对密钥。下面是邻节点的对密钥的建立过程:

(1)同一Cell内邻节点间对密钥建立

设 Cell＜i，j＞中节点 u 和 v分配的哈希值及下标如表2所示，对密钥建立步骤如下:

Step1: u— ＞*: { u，hide＜ i，j，x＞} ，u 为node＜ i，j，u ＞的ID。

Step2: v— ＞*: { v，hide＜ i，j，y＞}，v 为node＜ i，j，v＞的ID。

Step3: 接收到来自v的广播信息后，u 也接收到了节点v 的hide＜ i，j，y＞值。如果hide＜ i，j，y＞≤hide＜ i，j，x＞，节点u 计算V＜ i，j，y＞，V＜ i，j，y＞= Hx － y( V＜ i，j，x＞) ，x － y = hide＜ i，j，x＞－ hide＜ i，j，y＞，同时计算V＜ i，j，y＞°A＜ i，j ＞(u) 作为节点u 新的行向量A'(u); 如果hide＜ i，j，y＞＞hide＜ i，j，x＞，则V＜ i，j，x＞°A＜ i，j ＞(u) 作为节点u 新的行向量A'(u) 。最后由Blom 方案原理计算对密钥K＜ i，j ＞(u，v) = A'( u)·G＜ i，j ＞(v) 。

Step4: 同理v 计算V＜ i，j，x＞，将V＜ i，j，x＞°A＜ i，j ＞( v) 作为节点v新的行向量。最后计算对密钥)。

(2)邻Cell邻节点间对密钥的建立

该过程与前一个过程同时进行，网络节点部署后，按照随机密钥分配方案进行分配。设节点和，共同密钥为，这时 u和 v计算 x值，按一定顺序连接。u和v采用t次多项式xf(x，y)进行彼此密钥的分配。得共享密钥对为，有在计算出对密钥后，所有节点包括同一Cell内的节点立即删除所有存储的随机密钥。

2．2．3 路径密钥建立

该方案中同一个Cell中的邻节点总是能够直接建立对密钥的，因此路径密钥的建立主要指不同Cell间对密钥的建立，可以采用普通路径密钥建立方法来建立本方案的路径密钥。

3 性能分析

3．1 本地连通概率分析

本地连接概率(Local Connectivity)是指任意两个邻节点建立直接对密钥的概率，记为PLC，其中PLC=P(B(u，v)|A(u，v))，事件 A(u，v)表示 u，v是邻节点，事件B(u，v)表示直接建立对密钥。KDDK方案中能够保证同一个Cell内的任意邻节点建立直接对密钥，则同一Cell内的本地连接概率为1。由于任意两个不同Cell邻节点拥有从同一个密钥池中产生的 mR/3个密钥，因此可以得出

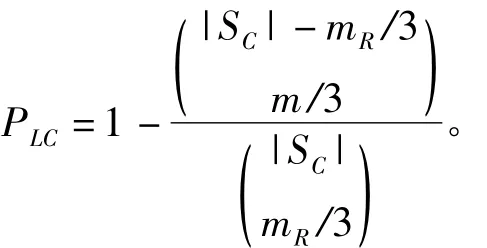
本文将与基于蜂窝的 Beibei Kong方案［11］和q-composite进行比较，本地连接概率分析结果如图3所示。Kong是Du［12］基础上提出的一个正六边形的基于部署知识的密钥分配方案，且在本地连接概率方面优于Du方案。本文如不特别声明默认网络由10×10的cell组成，即M=10，T=10。当Sc=2 000，4 000，Kong方案中两个相邻蜂窝间密钥池重叠因子 γ=0．125时，图3中可以看出KD－DK方案的本地连通概率方面略低于Kong提出的方案(仅局限于初始存储密钥数mR相同的前提下)，但远高于 q-composite方案。与 Kong和q-composite方案不同，本方案节点中存储的随机密钥在建立对密钥后被删除，因此网络初始化时存储密钥数mR对安全性和后面的存储空间几乎无影响，因而可以通过增加mR来提高节点本地连接概率。

假设节点在存储了Blom矩阵及其相关的数据后剩余存储空间为 C，设C=250，则可令 mR=C。当Sc=2 000，4 000时，KD－DK的本地连接概率分别可达到0．972 5和0．827 7。达到相同概率时Kong和q-composite方案各自需存储的密钥数mR如表3所示。虽然部署时Kong所需存储的密钥比KDDK小，但这耗尽了节点的大部分资源同时威胁到网络安全，这将严重影响节点后期功能，在实际中几乎不可能实现。而KD－DK中存储的随机密钥在后期将被删除，对安全性和存储空间几乎无影响，因此KD－DK可以实现Kong和q-composite方案不可能实现的更高的本地连接概率。

表3 Sc=2 000，4 000时，C=250时Kong和 q-composite所需存储的密钥数

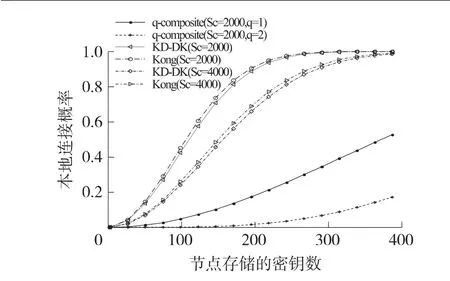
图3 本地连接概率分析

3．2 安全性分析

同一Cell哈希链的同一个哈希值分配给节点的个数不会超过λ，意味着同一个哈希值与矩阵A进行“°”运算产生同一个Blom矩阵的个数也不会超过λ个，说明同一Cell内节点间链路无法破解。而相邻Cell邻节点采用随机密钥的方案，由x=H(r1‖r2‖…‖rm)，可知，当相同的多项式 xf(x，y)个数超过t且被俘节点超过t个时，该多项式存在被攻破的可能。当且仅当超过t个节点共同含有相同的m个密钥，且这些节点共同的密钥数有且只有这m个密钥时，才满足上述被破解的前提条件。

定义3 概率p(i，k)p(i，k)表示有k个节点共同拥有且只拥有相同i个密钥的概率。由分配过程可推导出式(2):

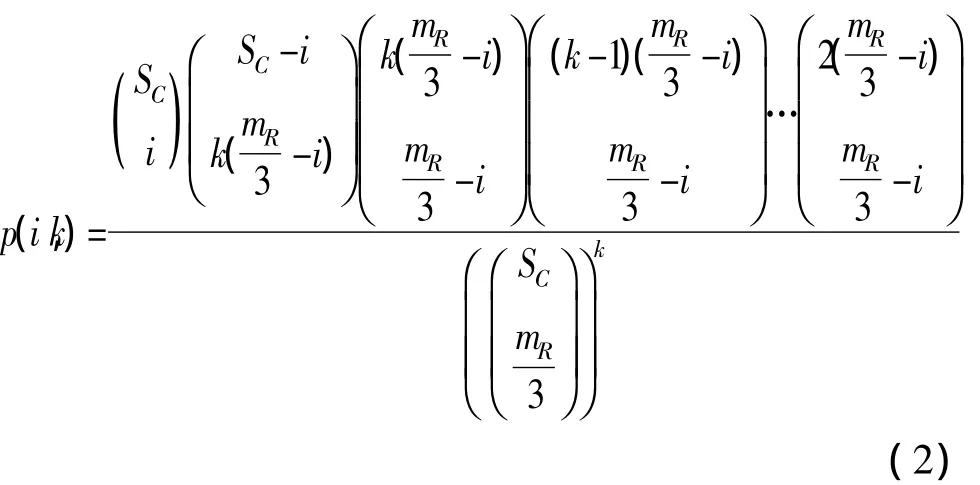
其中 i=1，2，…，mR/3，0≤k≤NC，NC为网络节点数。当且仅当k≥(t+1)时安全链路才有可能破解。p(i，k)越小则网络越难破解，网络的安全性也就越高。图4所示为SC=2000，mR=300p(i，k)的图形。

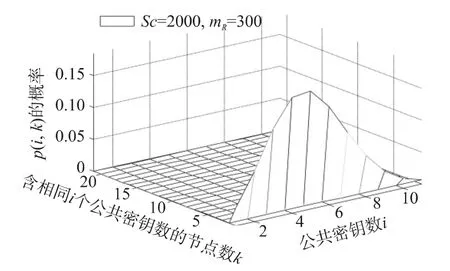
图 4 Sc=2 000，p(i，k)图形

当 SC=2000，mR=300 时，对所有的 i，p(i，2)＜1e－5，因此图4可以近似的认为 k＞3时，p(i，k)≈0，即有k个节点同时共享相同的i个且恰好只有共同的i个密钥的概率几乎为零，如图4中网格部分所示。也就是说产生k＞3个由相同数目的密钥产生而来的t次多项式的个数几乎不可能;当0≤k＜2，0≤i≤10 时，如图 4 斜面所示，p(i，k)在 i=5 时取得最大值，其中p(5，k)最大等于0．1847。但是网络安全链路只有当k≤(t+1)时才有被破解的可能，而前面已指出时k＞3，p(i，k)≈0。通常t的值可以设的更大，一般的网络只要t的不是太小(一般t＞20)，网络几乎不可攻破。

当 SC=2000，t=30，PLC分别为 0．33 和 0．5 时，KD－DK与Kong和q-composite的抗毁性能如图5和图6所示，其中Kong方案利用多项式在抗毁性上有改进［11］，为更清楚地表述，改进前后的方案分别用Kong1和Kong2标记。图5和图6中可以清楚地看到，KD－DK抗毁性明显优于Kong和q-composite方案，在这两种情况下节点被捕对链路安全性几乎没有影响。由图可得链路安全优劣存在有以下关系:KD－DK＞Kong＞q-compostie。在 q-compostie方案中当被捕节点数小于一个临界值时，q=2优于q=1时的方案;当被捕节点大于临界值时安全性劣于q=1时的方案，其中PLC=0．33该临界值约为700，PLC=0．5临界值约为600。理由是当q=2时达到相同的本地连接概率节点需要存储更多的密钥，因此大量节点被捕时，容易将主密钥池攻破。例如SC=2 000，PLC=0．33时，q-composite主密钥池大小等于SC×M×N=2×105，当q=1时节点只需存储约，282个密钥，而q=2时需要存储约483个密钥，密钥数量大幅增加，因而当捕获大量节点时主密钥池易攻破。

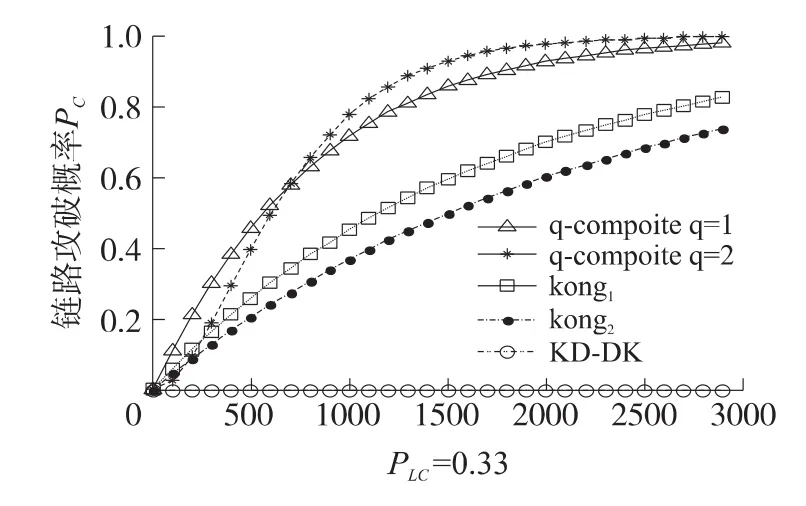
图5 PLC=0．33链路安全分析

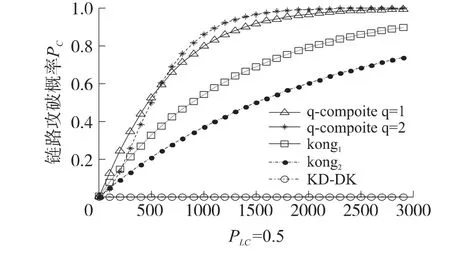
图6 PLC=0．5链路安全分析

3．3 空间开销

网络部署前节点需存储((λ+1)logq+1+mmR+(t+1)logp)bit密钥，节点对密钥建立后，由于节点删除了相关的随机密钥，则只需存储((λ+1)logq+1+(t+1)logp)bit密钥，m为单个预分配密钥的大小。这样在节点在对密钥建立后可以节约许多空间以存储其他的一些信息。因此网络可以通过调节mR以提高不同Cell邻节点建立对密钥的概率，而在后期又对节点的存储空间不产生影响，有较好的灵活性。

4 总结及工作展望

无线传感器网络的安全问题当限制当前传感器网络发展和应用的一个重要因素。本文在基于部署知识的基础上对Blom矩阵和随机密钥方案进行了改进，提出了一种新的密钥分配方案。对该方案进行了详细的阐述，并其性能进行了详细的分析。通过与Kong和q-composite方案比较，该方案在本地连接概率和抗毁性方面有显著改善。若节点在Tmin较小时有节点被捕获，密钥分配的安全性能仍需进一步研究。

［1］ Eschenauer L，Gligor V D．A Key-Management Scheme for Distributed Sensor Networks［C］//Proceedings of the 9th ACM Conference on Computer and Communications Security．ACM:Washington，DC，USA，2002:41 －47．

［2］ Chan H，Perrig A，Song D．Random Key Predistribution Schemes for Sensor Networks［C］//Proceedings of the 2003 IEEE Symposium on Security and Privacy．IEEE Computer Society，2003:197．

［3］ Tzu-Hsuan S，Chuan-Ming L．In Enhancing the Key Pre-distribution Scheme on Wireless Sensor Networks［C］//Asia-Pacific Services Computing Conference，2008．APSCC’08．IEEE，2008:1127－1131．

［4］ Du W，Deng J，Han Y S，et al．A Pairwise Key Pre-Distribution Scheme for Wireless Sensor Networks［C］//Proceedings of the 10th ACM Conference on Computer and Communications Security．Washington D．C，USA:ACM，2003:42 －51．

［5］ Camtepe S A，Yener B．Combinatorial Design of Key Distribution Mechanisms for Wireless Sensor Networks［J］．Networking，IEEE/ACM Transactions on，2007，15(2):346 －358．

［6］ Liu D，Ning P．Location-Based Pairwise Key Establishments for Static Sensor Networks［C］．//Proceedings of the 1st ACM Workshop on Security of Ad Hoc and Sensor Networks Fairfax，Virginia:ACM．2003:72 －82．

［7］ Taekyoung K，Jonghyup L，Jooseok S．Location-Based Pairwise Key Predistribution for Wireless Sensor Networks［J］．Wireless Communications，IEEE Transactions on，2009，8(11):5436 －5442．

［8］ Nguyen Xuan Q，Kumar V，Yunjung P，et al．A High Connectivity Pre-Distribution Key Management Scheme in Grid-Based Wireless Sensor Networks［C］//Convergence and Hybrid Information Technology，2008．ICHIT’08．International Conference on，2008:35 －42．

［9］ 彭保．无线传感器网络中利用部署知识的组合密钥预分发算法设计［J］．传感技术学报，2007，20(6):1376 －1380．

［10］姚宣霞．一种基于蜂窝模型的无线传感器网络密钥分配方案［J］．传感技术学报，2008，21(11):1923 －1928．

［11］ Beibei K，Hongyang C，Xiaohu T，et al．Key Pre-Distribution Schemes for Large-Scale Wireless Sensor Networks Using Hexagon Partition［C］．//Wireless Communications and Networking Conference(WCNC)，2010:1 －5．

［12］ Wenliang D，Jing D，Han Y．S，et al．In A Key Management Scheme for Wireless Sensor Networks Using Deployment Knowledge［C］//INFOCOM 2004．Twenty-third AnnualJoint Conference of the IEEE Computer and Communications Societies，2004:597．