压电微悬臂梁气体传感器静态弯曲模型的研究*

景大雷，王 飞* ，赵学增，王晓明(1．哈尔滨工业大学机电工程学院，哈尔滨150001;)2．哈尔滨工业大学微系统与微结构制造教育部重点实验室，哈尔滨150001

近年来，微悬臂梁传感器因其具有结构尺寸小、灵敏度高、响应频率快、批量生产成本低等优点，在生化传感器方面得到了广泛的应用［1－4］。微悬臂梁传感器有两种独立的工作模式:静态工作模式和动态工作模式［5－8］。对于表面镀有压电薄膜的微悬臂梁，由于压电材料具有的压电效应，使得压电微悬臂梁同时具有驱动和传感的特点，因此得到了越来越多的关注和应用，已经成为目前研究的热点。

用于生物和化学检测的压电微悬臂梁通常在其上表面镀一层对待测物质具有敏感作用的敏感层。敏感层吸附待测分子或原子后，会导致微悬臂梁产生弯曲或共振频率的变化，通过测量弯曲量或共振频率的改变量，达到物质传感检测的目的。目前为止，对于微悬臂梁静态传感方式的理论研究，大多数都采用比较直观的Stoney模型［9］作为理论上的分析手段。近年来，也有越来越多的研究小组采用能量的方法［10］从原子或分子层面研究吸附引起的微悬臂梁的静态理论模型。所谓能量的方法是指在吸附过程中，分子(原子)势能和微悬臂梁的弹性势能之间会产生相互转化。吸附稳定之后，系统总能量，即分子势能和梁的弹性势能之和，应为最低。总能量最低时梁的曲率半径即为所要求解的值。但是，由于分子或原子吸附会使微悬臂梁表面产生表面力，引起微悬臂梁吸附稳定后的中性层位置的变化。但是目前使用能量法在建模过程中，并没有考虑到由于分子或原子吸附在悬臂梁表面产生的表面应力所引起的微悬臂梁中性层位置的变化，因此会使建模结果产生误差。

本文将对压电微悬臂梁传感器静态模式进行研究，建立气体吸附压电悬臂梁静态弯曲模型。基于能量方法，以压电微悬臂梁为例，通过引入吸附表面应力引起的微悬臂梁中性层位置的变化，研究压电微悬臂梁吸附单层分子稳定后的弯曲情况，对传统的单纯基于能量法的悬臂梁静态模型进行了修正。结果表明在相同吸附表面积和吸附量条件下，压电微悬臂梁的曲率半径随梁厚度减小而减小，随梁杨氏模量的减小而减小;且微悬臂梁尺寸的越小，考虑中性层位置变化对静态变形影响越大;且压电层和基底层杨氏模量比值不同会使梁曲率半径随压电层与基底层厚度比呈现不同的变化趋势。

1 理论模型

1．1 中性层位置确定

本文中所采用的模型是表面吸附有单分子层的压电微悬臂梁。假设吸附在梁表面的第一层分子对悬臂梁的变形起到主要作用［11］。同时由于敏感层厚度远小于压电微悬臂梁厚度，故在建模过程中，忽略敏感层的影响。设被测分子在压电微悬臂梁表面吸附的简化模型如图1所示，并建立如图1所示坐标系。其中，x轴位于压电层与非压电层结合面处，z轴沿梁厚度方向，图中上层为压电层，下层为非压电层，P，Q，R 为被测分子或原子，而 1，2，3，4 为敏感层分子。

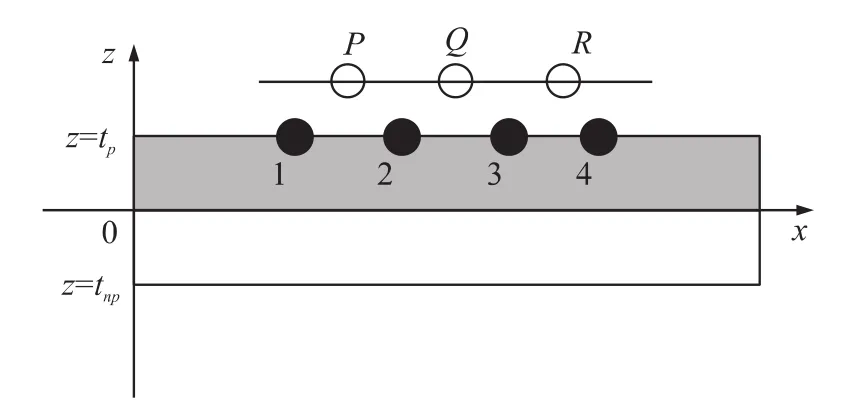
图1 被测分子在压电微悬臂表面的分布图

分子(原子)在压电微悬臂梁表面吸附后，压电微悬臂梁的上表面会产生表面应力。由于上下表面具有一定的应力差，会引起微悬臂梁的弯曲变形，同时在变形过程中会引起悬臂梁中性层位置的变化。

任取压电微悬臂梁自由端一部分。设分子吸附稳定之后，压电微悬臂梁上表面的表面应力为τ，并假设微悬臂梁压电层和非压电层内应力线性变化，如图2所示。

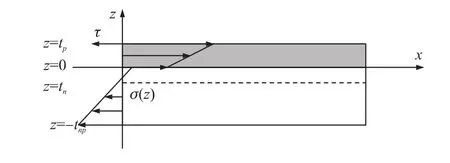
图2 压电悬臂梁自由端截取部分应力应变原理图

吸附变形后微悬臂梁的应变如式(1)所示

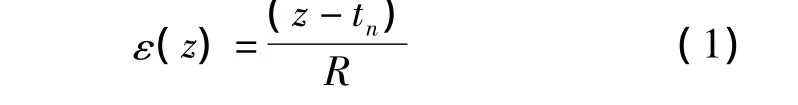
其中，tn为中性层位置，R为中性层曲率半径。

同时，微悬臂梁各处应力如式(2)所示

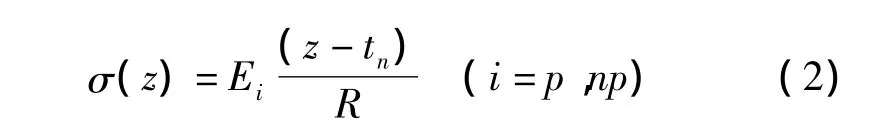
其中E为梁的杨氏模量。i=p表示压电层的杨氏模量，i=np表示非压电层的杨氏模量。

压电微悬臂梁吸附稳定之后，应满足如下平衡条件:

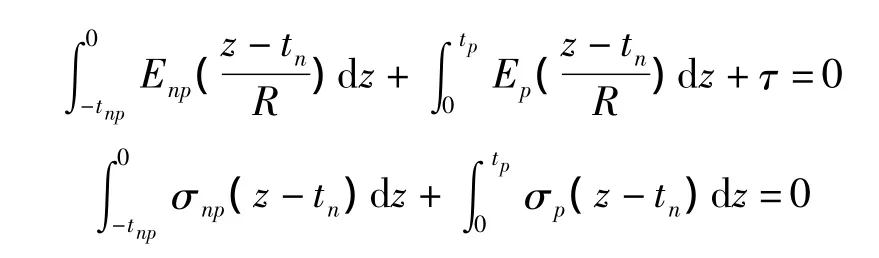
其中，tp代表压电层厚度，tnp代表非压电层厚度。

由以上两式分别可以计算出中性层位置tn，如式(3)、(4)所示。

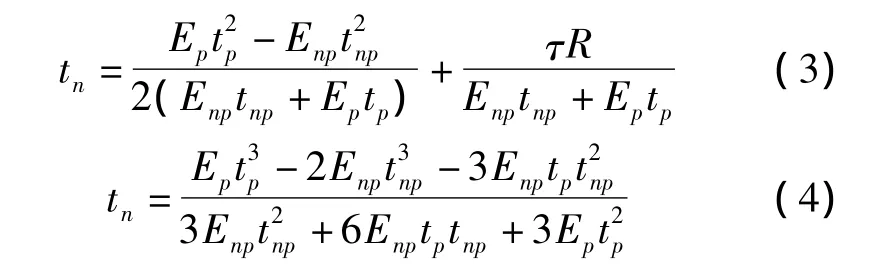
1．2 压电微悬臂梁曲率半径

压电微悬臂梁吸附分子达到稳定的过程之中，存在着能量之间的相互转化。被测分子本身的势能以及被测分子与敏感层之间的势能转化为压电微悬臂梁的弯曲势能。因此，压电微悬臂梁系统吸附平衡之后，被测分子本身的势能、被测分子与敏感层之间的势能以及压电微悬臂梁的弯曲势能三部分能量之和应该达到最小值。设压电微悬臂梁弯曲变形后分子排布如图3所示。

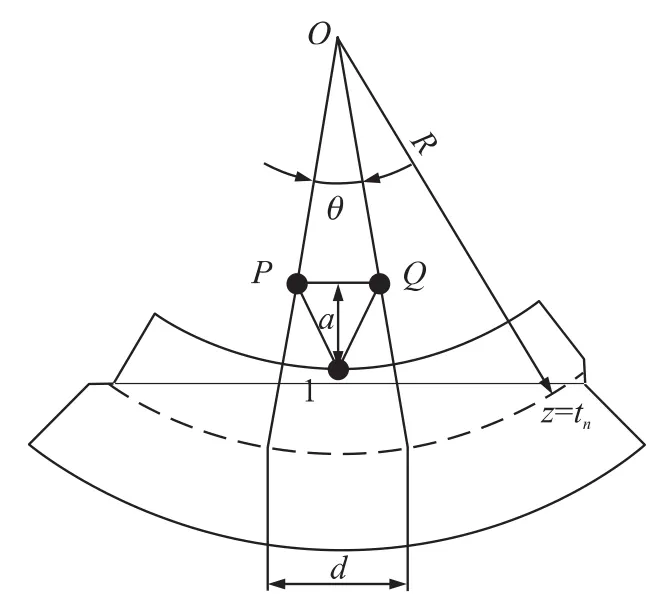
图3 压电微悬臂梁弯曲后分子排布图

分子吸附稳定后，分子之间距离发生变化。由图3几何关系可以得到，吸附稳定后相应分子之间距离如式(5)、(6)所示［10］。

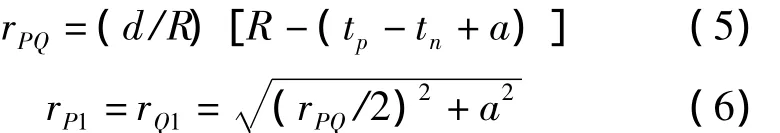
其中，dPQ为吸附稳定后被测分子之间的距离，dP1，dQ1为吸附稳定后被测分子与敏感层分子之间的距离，R为中性层处曲率半径，a为吸附层的高度。

吸附完成后，原子之间的势能，可以通过Lennard-Jones势能函数用曲率半径R表示，如式(7)所示［10］。

取一个吸附分子间距d的梁端作为研究对象，吸附稳定后，该段压电微悬臂梁应变能如式(8)所示。

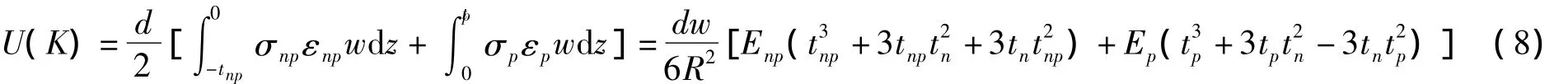
同时，该段压电微悬臂梁上总的分子势能如式(9)所示［12］。

其中，σ为该段压电梁上吸附的原子数，U0为吸附分子内部的势能，并假设在吸附整个过程中，吸附分子结构变化很小，可以忽略不计，则U0为常数。

吸附稳定之后，系统总能量为:

由前所述系统稳定后，应用系统总能量最低，即:

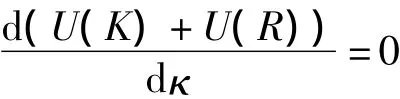
由上式可得曲率的方程为:

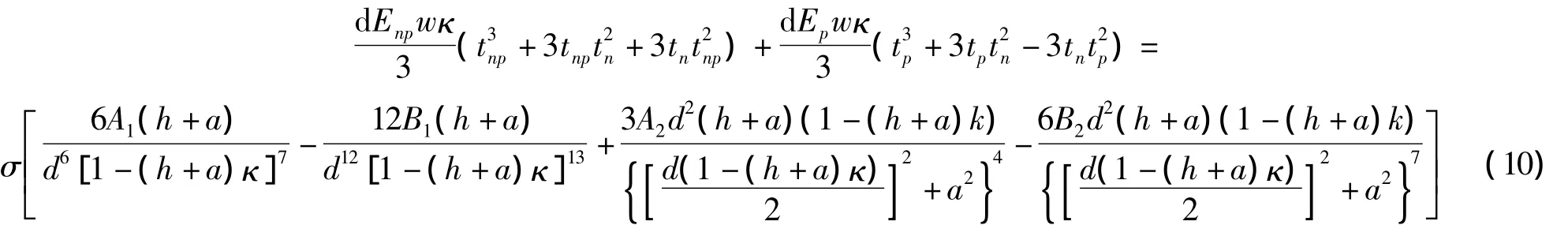
其中，κ=1/R为悬臂梁的曲率。由式(3)、(4)、(10)可得，吸附稳定后压电微悬臂梁的曲率半径和吸附引起的表面应力。

2 算例与数值计算

2．1 算例

本部分使用Dareing和Thundat的实验对所建立的理论模型进行验证。而所参照的实验所采用的是具有一种材料的微悬臂梁，所以在验证过程中应取tp=0。使用文献［10］中所给参考数据，采用式(4)、(10)可得 c/R=4．685 ×10－7，由微悬臂梁几何关系可知，自由端的变形量为δ=267．7 nm，与实验结果相比较具有较好的一致性。而理论模型结果与实验结果之间的差值可能是由于汞在微悬臂梁表面吸附时，排列不完全均匀，而且存在多层吸附引起的。若在建模过程中采用多个原子作为研究对象，结果与实验结果相比，更加准确。

2．2 数值计算

下面我们取一定尺寸的压电微悬臂梁带入模型公式进行计算。模型为使用镀有铝膜的压电微悬臂梁对水分子进行检测。首先确定公式中参数［12］:a取经验值即为铝原子晶格常数。L－J系数为:

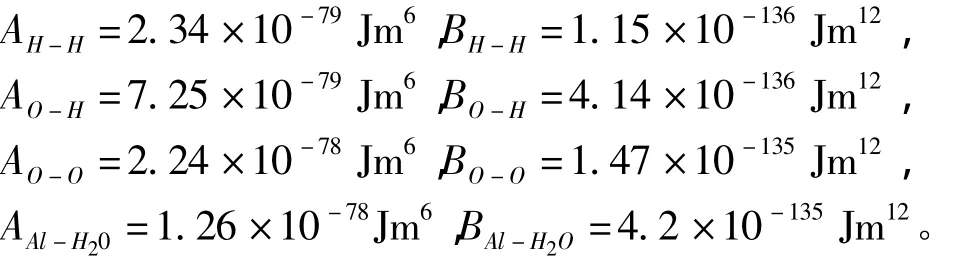
2．2．1 厚度对压电微悬臂梁静态变形的影响

设压电悬臂梁的 l=500 μm，ω =50 μm，Ep=104 GPa，Enp=165 GPa。分别采用本文所述理论模型与文献［10］中理论模型对吸附平衡后不同厚度压电悬臂梁的曲率半径进行计算，得到了如表1和图4所示的计算结果。

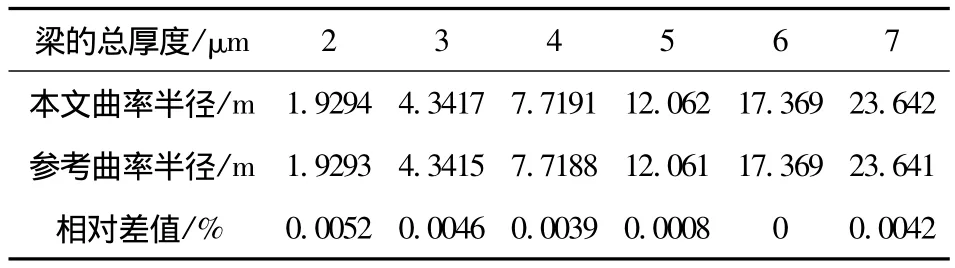
表1 不同厚度压电微悬臂梁吸附平衡后曲率半径(tp=tnp)

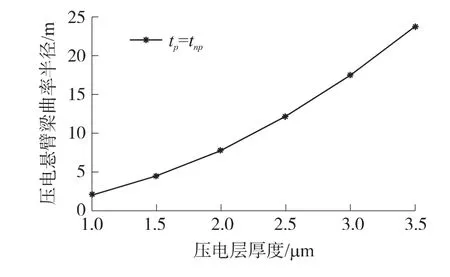
图4 压电微悬臂曲率半径与梁厚关系曲线

由表1及图4我们注意到，在相同吸附表面积和吸附量下，压电微悬臂梁曲率半径随梁厚度的增加而增加，即压电微悬臂梁的变形量随厚度的减小而减小。同时，由表1第四行我们可以看到，本文模型与参考模型计算结果差值很小。

为此，我们对压电悬臂梁的基本尺寸进行了修改，取 l=5 μm，ω =0．5 μm，总厚度值如表 2 所示，而其他参数保持不变。我们可以得到如表2和图5所示结果。

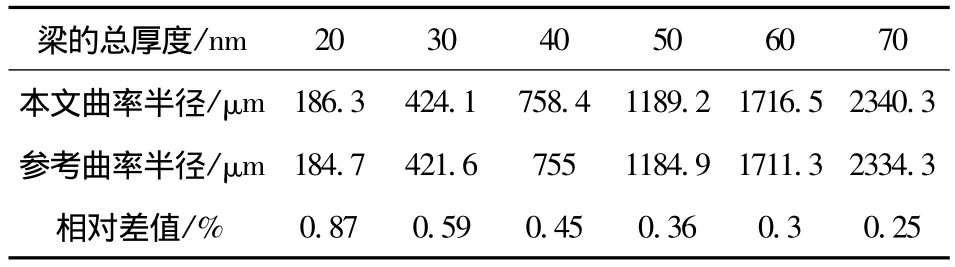
表2 不同厚度压电微悬臂梁吸附平衡后曲率半径(tp=tnp)

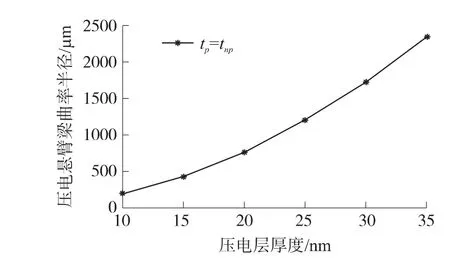
图5 压电微悬臂曲率半径与梁厚关系曲线

显然，通过表2和图5所示结果，我们可以得到与表1和图4类似的结论。同时我们可以注意到，当微悬臂的尺寸下降时，悬臂梁中性层位置的变化的引入，会引起计算结果较大的变化。因此中性层位置变化的引入，为更小尺度悬臂梁静态理论模型的研究提供了一定的改进和修正。

2．2．2 不同厚度比对压电微悬臂静态变形的影响

下面我们对具有不同厚度比δ(压电层与非压电层厚度比)的压电微悬臂梁进行研究，在数值计算过程中取 l=500 μm ，ω =50 μm，tp+tnp=5 μm，其他参数保持不变。采用本文所建立的模型对不同厚度比的压电微悬臂进行研究可以得到如图6所示的结果。

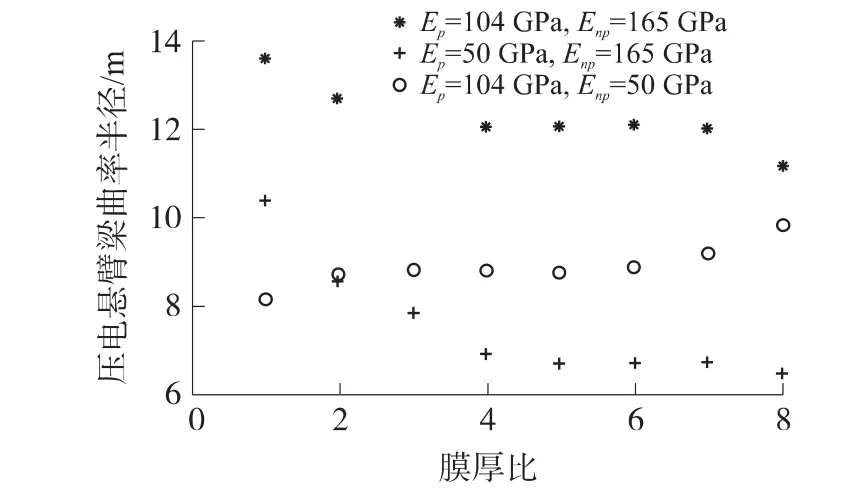
图6 压电微悬臂曲率半径与不同厚度比之间关系曲线

通过图6中三条变化曲线可以看到，在相同膜厚比条件下，压电微悬臂梁在吸附平衡后，压电微悬臂梁的曲率半径随压电梁各层杨氏模量的减小而减小，即压电微悬臂梁的变形量随压电微悬臂梁各层杨氏模量的减小而增大。

同时对图6中三条变化曲线研究发现，每条曲线均存在一个拐点。对于Enp=165 GPa的两条曲线，看以注意到两条曲线具有类似的变化规律，但两者拐点存在的位置不同，上面一条曲线拐点约在δ=6处，而下面一条曲线的拐点约在δ=7。而对于Enp=104 GPa的两条曲线，两者具有相反的变化规律，上面一条曲线拐点约在δ=6处，而下面一条曲线的拐点约在δ=3。同时分析不同曲线的材料杨氏模量比我们看到，这种拐点的存在，以及曲线的变化规律与材料的杨氏模量有关，即是由材料的性质决定的。

3 结论

本文基于能量法，并引入表面吸附引起的微悬臂梁中性层位置的变化，构建了单层分子在压电微悬臂梁表面进行吸附的静态理论模型，对传统的基于能量法的模型进行了改进，得到了吸附稳定后压电微悬臂梁的曲率半径公式和表面应力公式。同时利用文献中的实验进行验证，证实了所建立模型的合理性和准确性。进一步计算结果表面在相同吸附表面积和吸附量条件下，压电微悬臂梁的曲率半径随梁厚度减小而减小，随梁杨氏模量的减小而减小;而当压电微悬臂尺度减小时，悬臂梁中性层位置变化的引入对仅基于能量法的静态模型进行了修正;同时曲率半径随不同膜厚比变化过程中存在一个拐点，这一特殊点受到两种材料的杨氏模量的影响。该模型的建立为更小尺度悬臂梁的静态理论模型进行了修正，并为研究压电微悬臂梁动态模式在气体检测方面的应用打下了基础。

［1］ Chen G Y，Thundat T，Wachter E A，et al．Adsorption-Induced Surface Stress and Its Effects on Resonance Frequency of Microcantilevers［J］．J．Appl．Phys，1995，78(8):3618 －3622．

［2］ Chen G Y，Warmack R J，Huang A，et al．Harmonic Response Of Near-Contact Scanning Force Microscopy［J］．J．Appl．Phys，1995，78(3):1465－1469．

［3］ Chen G Y，Warmack R J，Thundat T，et al．Resonance Response of Scanning Force Microscopy Cantilevers［J］．Rev．Sci．Instrum，1994，65(8):2532 －2537．

［4］ Thundat T，Warmack R J，Chen G Y，et al．Thermal and Ambient-Induced Deflections of Scanning Force Microscope Cantilevers［J］．Appl．Phys．Lett，1994，64(21):2894 －2896．

［5］ Lu P，Lee H P，Lu C，et al．Surface Stress Effects on the Resonance Properties ofCantileverSensors［J］．Phy．Rev．B．2005，72，085405．

［6］ Huang G Y，Gao W，Yu S W．Model for the Adsorption-Induced Change in Resonance Frequency of a Cantilever［J］．Appl．Phys．Lett．2006，89，043506．

［7］ Zhang J Q，Yu S W，Feng X Q．Theoretical Analysis of Resonance Frequency Change Induced by Adsorption［J］．J．Phys．Lett．2008，41，125306．

［8］ YI X，Duan H L．Surface Stress Induced by Interactions of Adsorbates and Its Effect on Deformation and Frequency of Microcantilever Sensors［J］．J．Mech．Phys．Solids．2009，57(8):1254 －1266．

［9］ Muller P，Kern R．About the Measurement of Absolute Isotropic Surfaces of Crystal［J］．Surf．Sci．1994，301(1 － 3):386 － 398

［10］ Darling Don W，Thomas Thundat．Simulation of Adsorption Induced Stress of a Micro-Cantilever Sensor［J］．J．Appl．Phys，2005，97(4):3526－1－3526－5．

［11］ Martinez R E，Augustyniak W M，Golovchenko J A．Direct Measuremrnt of Crastal Surface Stress［J］．Phy．Rev．Lett．1990，64(9):1035－1038．

［12］刘笑笑，黄庆安，于虹．水分子诱致的纳米悬臂梁的弯曲模型［J］．传感技术学报，2008，2(21):195 －198．