平板表层缺陷检测涡流阵列传感器的设计

刘 波，罗飞路，侯良洁

(国防科技大学机电工程与自动化学院，长沙410073)

涡流阵列(Eddy Current Array，ECA)检测技术是涡流无损检测技术中新兴的技术分支，它是通过检测传感器结构的特殊设计，运用计算机技术和数字信号处理技术，实现对材料和零部件的快速、有效地检测［1－3］。涡流阵列传感器是阵列检测仪器的重要组成部分，其设计的优劣在很大程度上制约着检测仪器的灵敏度和空间分辨率［4－6］。

最初的阵列传感器均由绕制的线圈构成。1988年，Krampfner Y D和Johnson D D将计算机辅助设计应用于涡流传感器设计，并制作了柔性阵列传感器，提高了检测的可靠性［7］。1991年，加拿大Podney W N和Czipott P V制作了微SQUID阵列传感器，大大缩小了传感器线圈尺寸，该传感器检测水平精度1 mm，垂直精度 0．3 mm［8］。1991 年，Melcher JR提出了线圈磁力计阵列传感器［9］。2000年，Yashan A等研制了巨磁阻阵列传感器。2001年，中国哈尔滨工业大学李德胜等提出了霍尔传感器阵列，将霍尔器件用于磁测量。2004年，CODECI传感器问世，该传感器将阵列传感器与CCD结合，能够实时检测各种合金表面缺陷，缺陷深度检测精度可达0．2 mm［10］。CODECI传感器开启了阵列传感器与其他检测方法在信息获取层的集成，代表了阵列传感器发展的最高水平。

在涡流阵列传感器设计理论研究方面，2003年，日本学者Huang H运用数值计算方法对核电站蒸汽管道检测用涡流阵列传感器的线圈单元参数进行了优化［11］。2008年，Zaoui A应用简化的体积分法对阵列电磁场展开了研究，有效地缩短了缺陷检测正问题、逆问题的数值计算时间，解决了有限元、三维体积分法对阵列传感器仿真中的关键问题－划分单元、节点太多，计算非常耗时，为阵列传感器的设计提供了理论依据［12］。

本文采用有限元数值计算方法，以检测灵敏度、空间分辨率和线圈单元组有效检测区域比率等评价指标为依据，对平板表层缺陷检测涡流阵列传感器线圈单元内径、外径、高度等参数，线圈单元中心距，线圈单元排布方式进行了设计。

1 理论基础

涡流传感器按感应方式分类，可分为自感式传感器(或称参量式传感器)和互感式传感器(或称变压器式传感器)，按照检测比较方式可分为绝对式传感器和差动式传感器。涡流阵列传感器所有线圈单元覆盖面积较大，且根据受检对象形状排布各异，仅含一个激励线圈以产生适宜涡流检测的激励场难度很大、成本昂贵，因此现有的阵列传感器大多为所有线圈单元采用同一尺寸，既可为激励线圈又可为检测线圈。另外，互感式传感器在检测灵敏度和信噪比优于自感式传感器［13］。在检测比较方式上，由于考虑到差动式传感器对受检件长而平缓的缺陷可能漏检，且易产生难以解释的信号，因此大多采用绝对式传感器。

互感式传感器涡流检测的数值计算方法有两种:一，利用解析法计算导体板上不同放置方式的双线圈探头二端口互阻抗计算公式，该计算公式由劳伦兹互易定理推出，具体可参考文献［14］，二，用有限元方法和积分方法计算检测线圈感应电压。假设检测线圈径向有m层，轴向有n层，圆环P(i，j)表示其在径向位于第i(1≤i≤m)层，轴向位于第j(1≤j≤m)层，计算检测线圈单元感应电压可分为如下步骤:首先，建立有限厚平板单缺陷物理模型，设置激励线圈为载压绞线圈，求解激励线圈作用下检测线圈圆环P(i，j)内磁场分布;然后，用积分方法计算圆环P(i，j)所交链的磁链Ψi，j;其次，由法拉第电磁感应定律 u(t)=dΨ(t)/d t，求得圆环 P(i，j)的感应电压;再次，重复上述步骤求取检测线圈单元其他圆环的感应电压;最后，叠加所有圆环的感应电压，求得检测线圈单元的总的感应电压。

2 检测灵敏度

检测灵敏度是衡量涡流传感器检测性能的重要指标之一，能够较好地反映传感器对于缺陷的检出率。设定仿真物理模型:假定待测试件的电导率σ=3．82 ×107S/m，相对磁导率 μr=1，厚度 d=3．0 mm，包含长 lc=12 mm，宽 wc=1．0 mm，深 dc=1．2 mm的表面缺陷，其电导率σ=0，相对磁导率μr=1。将由缺陷引起的检测线圈单元感应电压的相对变化S定义为线圈单元的检测灵敏度。

其中，Vd为检测线圈单元通过缺陷的感应电压，Vn为检测线圈单元在无缺陷处的感应电压。下面对线圈单元中心距、线圈单元平均半径、线圈单元高对检测灵敏度的影响进行研究。

(1)线圈单元中心距

线圈单元内半径 r1=0．75 mm，外半径 r2=3．5 mm，高 h=3．0 mm，提离 l1=1．0 mm，检测频率f=5 kHz。激励线圈单元和检测线圈单元中心距D从8．0 mm增加到16．0 mm。线圈单元检测灵敏度S与两线圈单元中心距D的关系曲线如图1所示。观察图1可知，随着中心距的增大，检测线圈单元感应电压幅值变化单调递减，检测灵敏度先增后减，在中心距大约为12．8 mm时达到最大。

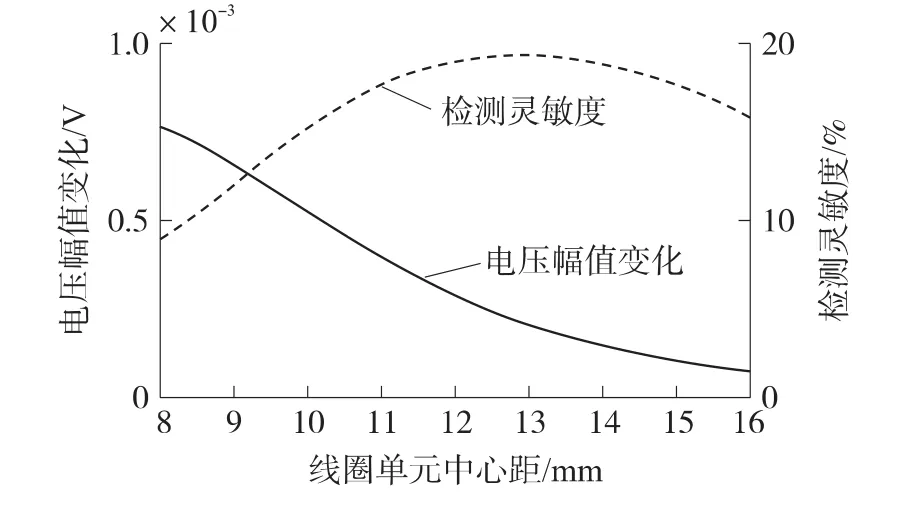
图1 检测灵敏度与线圈单元中心距的关系曲线

(2)线圈单元平均半径

线圈单元的匝数密度保持不变，高h=3．0 mm，内径r1从0．75 mm 增加到3．75 mm，外半径r2从3．5 mm增加到6．5 mm，平均半径r=(r1+r2)/2，提离l1=1．0 mm，检测频率f=5 kHz，激励线圈单元和检测线圈单元中心距D=14．0 mm。线圈单元检测灵敏度S与平均半径r的关系曲线如图2所示。由图2可知，随着线圈单元平均半径的增大，检测线圈单元感应电压幅值变化单调递增，检测灵敏度单调递减。

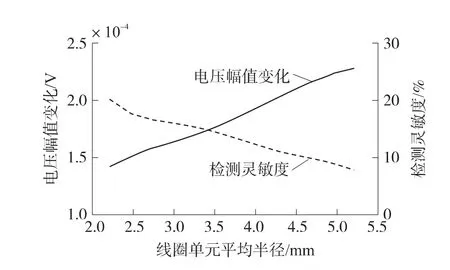
图2 检测灵敏度与线圈单元平均半径的关系曲线

(3)线圈单元高

线圈单元内半径 r1=0．75 mm，外半径 r2=3．5 mm，提离 l1=1．0 mm，检测频率 f=5 kHz。激励线圈单元和检测线圈单元中心距D=14．0 mm，高h从1．0 mm增加到5．0 mm。线圈单元检测灵敏度S与高h的关系曲线如图3所示。由图2可知，随着线圈单元高度的增大，检测线圈单元感应电压幅值变化单调递增，检测灵敏度单调递减。

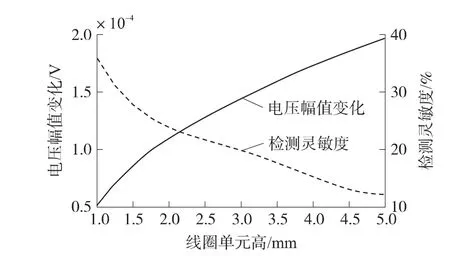
图3 检测灵敏度与线圈单元高度的关系曲线

3 空间分辨率

空间分辨率(Spatial Resolution)是反映涡流阵列传感器对于邻近的多个缺陷的检出能力的一项指标。平板、缺陷和线圈单元参数如第2节所述，缺陷1和缺陷2距离6 mm，在线圈单元匝数密度不变的情况下，改变线圈平均半径。扫描路径如图4所示，记扫描路径为X轴线，两缺陷沿X轴的中心点位坐标原点，检测线圈单元感应电压幅值变化如图5所示。由图5可知，线圈单元平均半径越大，缺陷处电压幅值变化与两缺陷中心处(即原点)的电压幅值变化越接近，两个缺陷越难于识别。因此，线圈单元平均半径越大，涡流阵列传感器的空间分辨率越小。

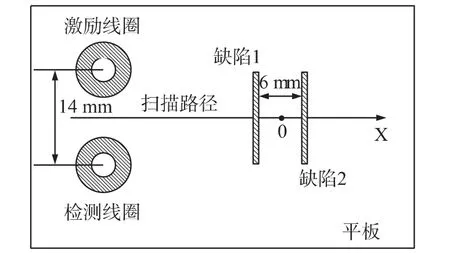
图4 传感器空间分辨率测试物理模型

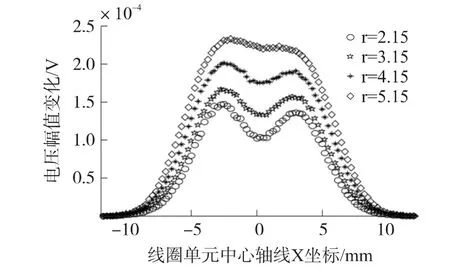
图5 不同线圈平均半径两邻近缺陷的检测曲线

4 线圈单元组有效检测区域比率

涡流阵列检测由于没有机械扫描装置和线圈单元数量等因素的制约，缺陷检测时总会存在一些灵敏度较低的区域，日本学者Huang H定义这些区域为涡流阵列传感器不敏感区域(Less Sensitive Zone)［6］。基于此，本文提出了线圈单元组有效检测区域比率(Efficient Detecting Zone Ratio of Coil U-nit Group)的概念，并作为一项性能评价指标引入了阵列传感器线圈单元排布方式的设计。

通常，涡流阵列传感器有如下两种排布方式:矩阵型和交错型。矩阵型阵列传感器可看作四线圈单元组的扩展，该类型传感器的单元组和单元组覆盖区域如图6(a)所示;交错型阵列传感器可看作多个三线圈单元组的扩展，其单元组和单元组覆盖区域如图6(b)所示。

图6 不同排布方式的涡流阵列传感器

线圈单元组有效检测区域比率γ作如下定义:在一定的检测灵敏度条件下，单元组对受检件有效检测区域Ae与单元组覆盖区域面积Ac的比率。

不难看出，该参数与检测灵敏度、线圈单元参数、传感器排布方式、受检件和缺陷等密切相关。该比率越大，表明阵列传感器对于覆盖区域检测能力越强，不敏感区域越小，理想的阵列传感器单元组有效检测区域比应接近于1，以保证无漏检情况。

为了简化研究，不妨假设一标准缺陷。有限元计算中，可将标准缺陷放置于受检件不同深度、不同位置，计算检测线圈感应电压变化，从而得到受检件在该次计算中的检测灵敏度。标准缺陷等物理参数的设置取决于研究者对于涡流检测长、宽、深方向的精度要求。本文标准缺陷长宽深取值1．0 mm×1．0 mm ×0．3 mm，检测灵敏度0．5%。利用多种激励检测方式，计算了不同线圈单元中心距、四个深度条件下，矩阵型和交错型涡流阵列传感器的线圈单元组有效检测区域比率。

(1)矩阵型涡流阵列传感器

完成图6(a)中矩阵型涡流阵列传感器单元组的检测可运用如下五种检测方式:线圈单元1激励，线圈单元2检测;线圈单元1激励，线圈单元3检测;线圈单元1激励，线圈单元4检测;线圈单元2激励，线圈单元4检测;线圈单元3激励，线圈单元4检测。表1为综合五种检测方式后，得到的矩阵型涡流阵列传感器的线圈单元组有效检测区域比率。hc为标准缺陷沿受检件深度方向坐标值。

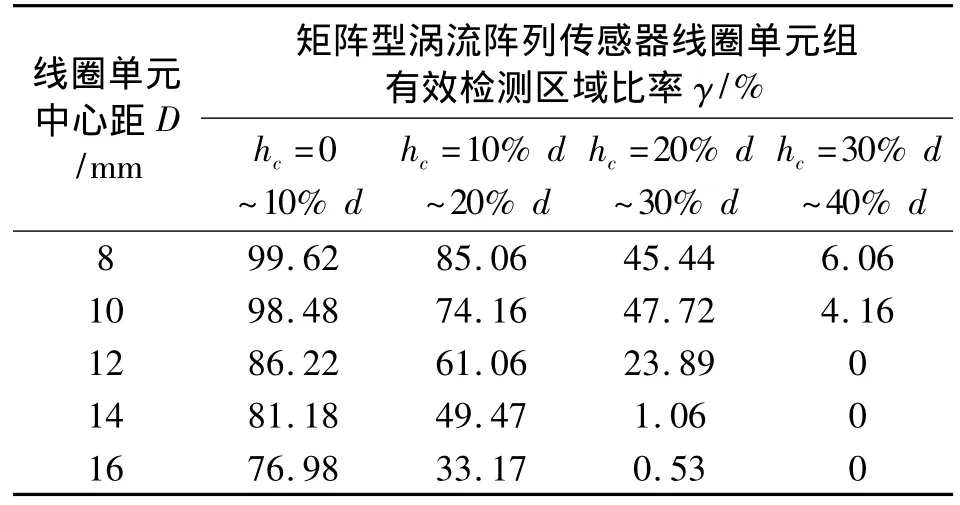
表1 矩阵型涡流阵列传感器的γ

(2)交错型涡流阵列传感器

完成图6(b)中矩阵型涡流阵列传感器单元组的检测也可运用五种检测方式:线圈单元6激励，线圈单元1检测;线圈单元6激励，线圈单元2检测;线圈单元5激励，线圈单元6检测;线圈单元6激励，线圈单元7检测;线圈单元1激励，线圈单元2检测。表2为交错型涡流阵列传感器的线圈单元组有效检测区域比率。

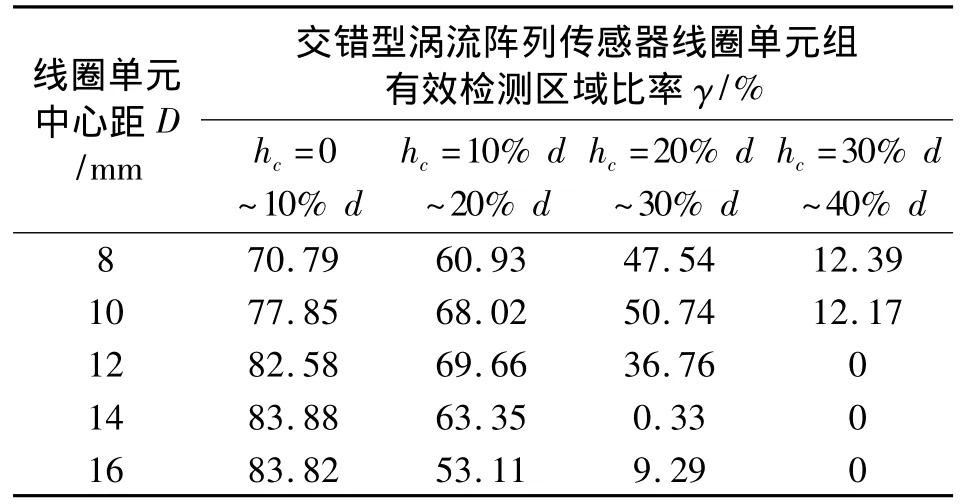
表2 交错型涡流阵列传感器的γ

交错型阵列传感器相邻两个单元组覆盖区域存在重叠区域，如图6(b)所示，不妨称为叠加检测区域。对叠加检测区域的线圈单元组有效检测区域比率进行数值分析，得到表3。

表3 交错型涡流阵列传感器叠加检测区域的γ

综合表1－表3可知，相同深度条件下交错型涡流阵列传感器叠加检测区域的γ基本上均大于矩阵型涡流阵列传感器的γ，矩阵型涡流阵列传感器的γ基本上均大于交错型涡流阵列传感器的γ。因此，相同检测条件下，交错型涡流阵列传感器相邻单元组叠加方式不敏感区域最小，漏检可能也最小。

5 实验验证

基于上述分析，制作了涡流阵列传感器，排布方式如图7中所示。所有线圈单元尺寸均相同，外径3．5 mm，内径1 mm，高3 mm。线圈单元组呈等边三角形分布，线圈单元中心距为10 mm。

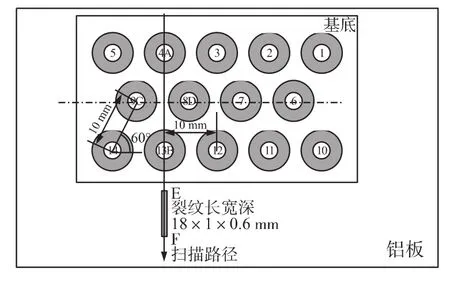
图7 涡流阵列传感器示意图

运用该阵列传感器对图7所示裂纹进行检测，得到图8检测结果。图8(1)为竖直列检测模式线圈单元4激励，线圈单元13检测同宽同深不同长度的沿扫描方向的两个裂纹并经平滑滤波后波形;图8(2)为水平行检测模式线圈单元9激励，线圈单元8检测波形;图8(3)为右上列检测模式线圈单元9激励，线圈单元4检测波形;图8(4)为右下列检测模式线圈单元9激励，线圈单元13检测波形;图8(5)为左上列检测模式线圈单元8激励，线圈单元4检测波形;图8(6)为左下列检测模式线圈单元8激励，线圈单元13检测波形。从图8中可以，依据研究结果制作的阵列传感器对于平板表层缺陷检测效果较好。

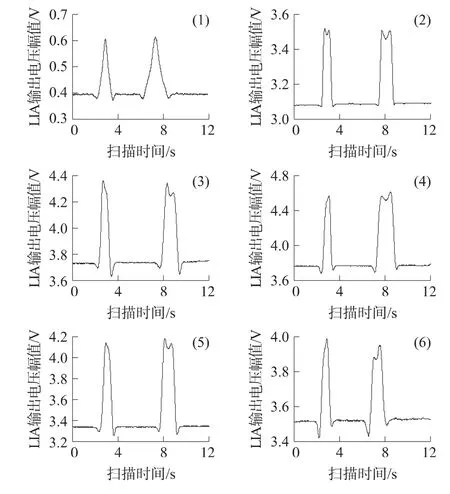
图8 六种激励检测模式检测结果

6 结论

本文采用有限元数值计算方法，提出了以检测灵敏度、空间分辨率、线圈单元组有效检测区域比率的涡流阵列传感器设计方案，得到如下结论:

(1)相同检测条件下，线圈单元平均半径越小，线圈单元高越小，检测灵敏度越大;线圈单元中心距与检测灵敏度成先递增后递减的关系，在接近且小于4倍的线圈单元外径处检测灵敏度存在一极值点。

(2)相同检测条件下，线圈单元平均半径越大，涡流阵列传感器的空间分辨率越小。

(3)相同检测条件下，交错型涡流阵列传感器相邻单元组叠加方式不敏感区域最小，漏检可能也最小。

(4)提出了与涡流阵列检测不敏感区域相关的参数——线圈单元组有效检测区域比率，基于该参数进行了涡流阵列传感器排布方式的设计优化。

［1］ Goldfine N，Zilberstein V，Washabaugh A，et al．Eddy Current Sensor Networks for Aircraft Fatigue Monitoring［J］．Material Evaluation，2003，61(7):852 －859．

［2］ Butin L，Wache G，Perez L，et al．New NDE Perspectives with Magnetoresistance Array Technologies-From Research to Industrial Applications［J］．Insight，2005，47(5):280 －284．

［3］ Crouch A E，Goyen T，Porter P．New Method Uses Conformable Array to Map External Pipeline Corrosion［J］．Oil and Gas Journal，2004，102(41):55 －59．

［4］ Jean-Francois Bureau，Robert C Ward，Wade Jenstead．Advances in Eddy Current Array Sensor Technology［C］．17th World Conference on Nondestructive Testing，Shanghai，China，2008，10:25 －28．

［5］ 张玉华，孙慧贤，罗飞路，等．一种用于盘孔裂纹检测的差动式涡流探头的设计与实现［J］．传感技术学报，2008，21(6):1079 －1083．

［6］ 任吉林，刁海波，唐继红，等．涡流传感器提离效应的ANSYS模拟［J］．传感技术学报，2008，21(6):967 －971．

［7］ Krampfner Y D，Johnson D D．Flexible Substrate Eddy Current Coil Arrays［C］．Review of Progress in Quantitative NDE，1988(7A):471－478．

［8］ Podney W N，Czipott P V．An Electromagnetic Microscope for Eddy Current Evaluation of Materials［J］．IEEE Transactions of Magnetics，1991，27(2):3241 －3244．

［9］ Melcher JR．Apparatus and Methods for Measuring Permeability and Conductivity in Materials Using Multiple Wavelength Interrogations［P］．US，5015951，1991，04．

［10］ Sollier T，Lorecki B，Goupillon O．CODECI，a New System for the Inspection of Surface Breaking Flaws Based on Eddy Current Array Probe and High Resolution CCD Camera［C］．ENDE’2003 Workshop Proceedings，IOS Press，2004:215 －222．

［11］ Huang H，Sakurai N，Takagi T，et al．Design of an Eddy-Current Array Probe for Crack Sizing in Steam Generator Tubes［J］．NDT and E International，2003，36(7):515 － 522．

［12］ Zaoui A，Menana H，Feliachi M，et al．Generalization of the Ideal Crack Model for an Arrayed Eddy Current Sensor［J］．IEEE Transactions on Magnetics，2008，44(6):1638 －1641．

［13］ Fukutomi H，Hashimoto M，Takagi T，et al．Performance Assessment of Mutual Induction Type ECT Probe by 3-D eddy Current Analysis［J］．Nonlinear Electromagnetic Systems，Studies in Applied Electro-Magnetics and Mechanics，IOS Press，1996，10:724 －727．

［14］ Burke S K，Ibrahim M E．Mutual Impedance of Air-Cored Coils A-bove a Conducting Plate［J］．Journal of Physics D:Application Physics．2004，37:1857 －1868．