边界节点对无线传感器网络连通性的影响*

张 强，孙雨耕，刘丽萍

(天津大学电气与自动化工程学院，天津300072)

无线传感器网络自兴起以来，在理论研究和应用技术等方面都取得了长足的进步，随着无线传感器网络实用化进程的不断推进，最初的设想正逐步成为现实，在各个应用领域中发挥作用。在无线传感器网络中，连通性是网络进行可靠数据传输的基础，也是网络正常运行的必要条件。对于一个有限的监测区域，处于区域边界的节点，与处于区域内部的节点相比，其邻居节点数要相对较小，从而影响网络的整体连通性。这种影响是由于无线传感器网络监测区域的有限性引起的，也体现在网络覆盖、路由、能耗等多方面，称为无线传感器网络的边界效应［1］。

边界效应也存在于无线Ad Hoc网络，早期的研究主要是针对无线Ad Hoc网络，例如为了消除边界效应对网络整体连通度的影响，Bettstetter在网络仿真验证过程中，分别采用了只考虑内部区域节点所形成网络的连通度或者用环面距离(Toroidal Distance)标识节点间的距离等方法，得到了与理论分析相一致的仿真结果［1－4］。但是对于无线Ad Hoc网络和传感器网络而言，除非当网络监测区域的面积无限大时，网络不会产生边界效应，否则网络边界是真实存在的，其产生的边界效应也是不可回避的，为此，Brust引入网络密度和有效覆盖面积的概念，分析了网络仿真中的边界效应，并给出了一个边界效应修正函数［5］，但是未对网络的整体连通性做进一步的研究。此外，还有一些文献对边界效应下的网络覆盖连通问题进行了研究［6－10］，例如Jin对无线传感器网络边界效应下的m－覆盖、n－连通问题进行了研究，并提出了相关的路由算法［7－9］。

本文对边界节点的有效通讯面积、邻居节点数和网络的整体连通性进行了理论分析，而后通过仿真分析，研究了边界节点对网络连通度分布、连通度期望以及网络是k点连通概率的影响。

1 网络模型

本文所采用的网络模型为几何随机图模型G(n，rC)［11］，其中 n 为网络的节点数，rC表示节点的通讯半径。针对连通性问题的研究需要，进一步对无线传感器网络做以下假设:

①无线传感器网络节点随机分布在的正方形监测区域S内，区域面积A=l×l，节点坐标(X，Y)在S区域内服从均匀分布，其概率密度函数为:

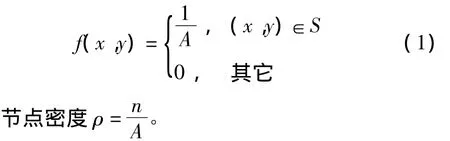
②节点通讯链路模型采用0/1模型。节点采用全向天线通讯，aik为节点i对节点k的通讯强度，可表示为:

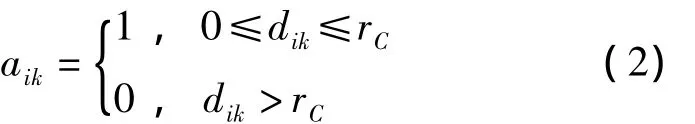
③除sink节点外，其他所有节点都是同构的。节点部署后，sink节点和其它所有节点均呈静态。

④网络的边界区域如图1中阴影部分所示，其面积为S(B)=l2－(l－2rC)2，位于边界区域的节点称为边界节点。

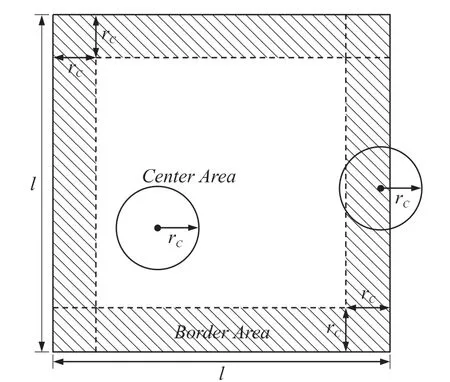
图1 无线传感器网络中的边界区域和边界节点

2 边界节点的连通性分析

2．1 边界节点的有效通讯面积

定义1 节点的有效通讯面积:节点通信区域与网络监测区域交集的面积，用Se表示。

对于内部节点，Se(C)=πr2C;对于边界节点，先将边界区域划分为两类B1和B2，如图2(a)所示。

图2 边界节点的有效通讯面积

在图2(b)中，位于B1类边界的节点有效通讯面积为:

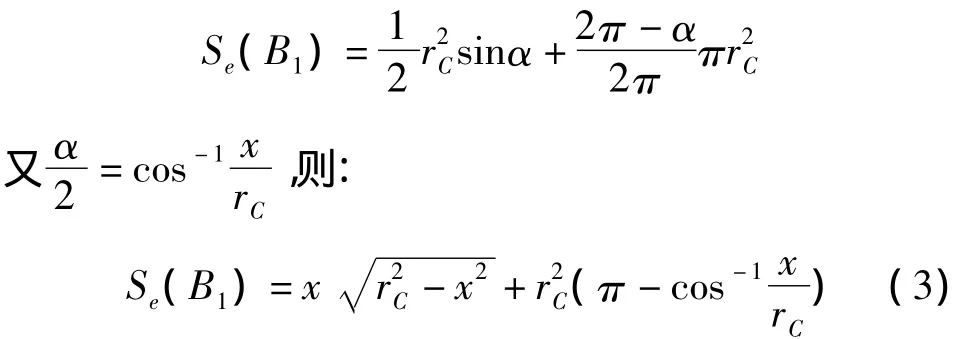
对于位于B2类边界的节点，分两种情况讨论，如图2(c)、(d)所示。

在图2(c)中，边界节点的有效通讯面积为:

各类边界节点有效通讯面积的数学期望分别为:

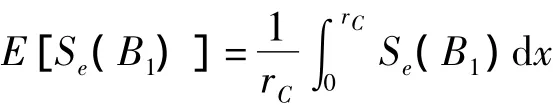
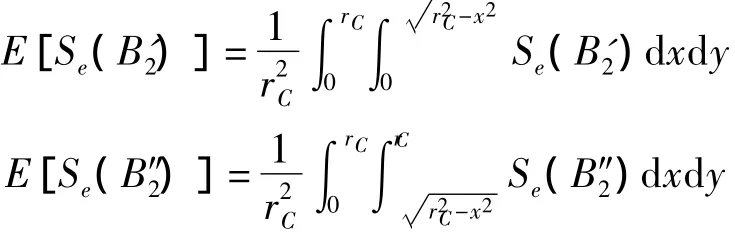
节点在监测区域内服从均匀分布，则各类边界节点的概率分别为:

则边界节点有效通讯面积的数学期望为:

2．2 边界节点的邻居节点数

对于随机均匀分布于面积为A的区域内的n个节点，文献［3］给出了在A0区域内恰好存在n0个节点的概率为:

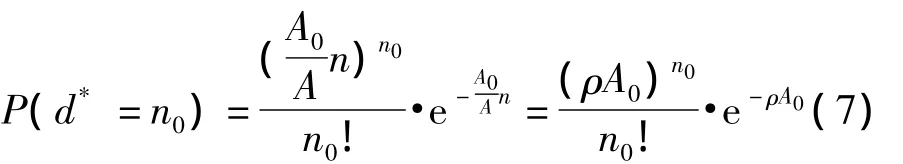
因此，在边界节点的期望有效通讯面积内，恰好存在n0个节点的概率，也就是一个边界节点的邻居节点数恰好为(n0－1)的概率为:

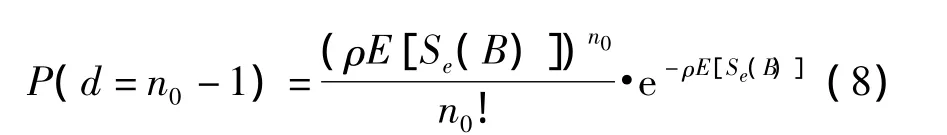
令n0=1，则一个边界节点成为孤立节点的概率为:

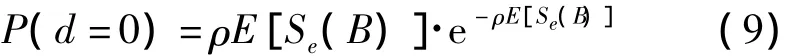
边界节点的邻居节点数期望为:

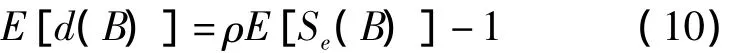
与边界节点相比，因为 E［Se(C)］=πr2C，所以内部节点的邻居节点数期望为:

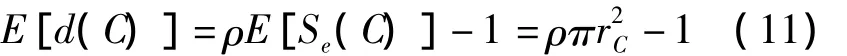
3 网络连通性及仿真分析

3．1 网络的连通性分析

对于整个无线传感器网络而言，节点有效通讯面积的数学期望为:

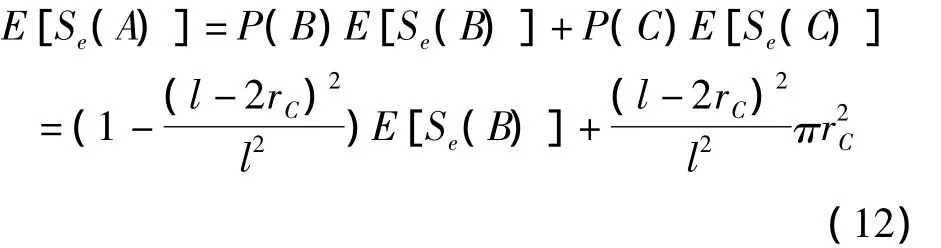
一个节点的邻居节点数恰好为(n0－1)的概率为:

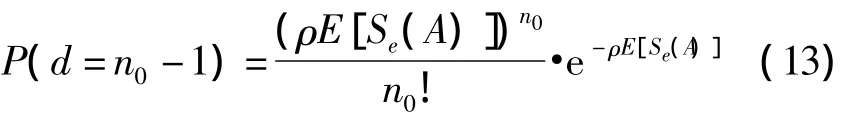
由此可以推导出，网络的最小度δ大于等于n0的概率为:

对于网络中每个节点至少存在k个相邻节点，也就是网络的最小度δ≥k的情况，由于κ(G)≤λ(G)≤δ(G)(网络的点连通度小于等于边连通度且两者均小于等于最小度)，所以网络是k点连通的概率可用下式表示:

根据文献［3］的理论推导结果，得到当n≫1，P(δ≥k)→1 时，

3．2 仿真分析

本文选择在100×100的正方形监测区域内对无线传感器网络进行仿真。在监测区域内多次抛撒节点形成无线传感器网络，求出每次抛撒所形成的无线传感器网络连通度，再进行统计分析，网络连通度的计算和统计分析采用文献［12］使用的方法。本文在仿真过程中将边界节点对网络连通度的影响与消除边界效应后的网络连通度情况进行了对比分析，通过文献［3］所使用的环面距离(Toroidal Distance)来标识上下左右边界区域间节点的距离，以达到消除网络边界效应的目的。

设节点通讯半径rC=20，逐步增加网络节点数量，取n=20～100，本文从以下几个方面仿真分析了边界节点对网络连通性的影响:

(1)边界节点对网络连通度分布的影响

通过仿真，得到 n=20，40，60，80，100 的网络连通度分布如图3所示，随着监测区域中节点数的增加，网络形成较高连通度的概率增加。但是边界节点的存在使网络形成较高连通度的概率降低，例如当n=100，网络中存在边界节点，该网络的连通度为3的概率为0．089 8，如图3(a)所示;消除网络的边界效应，则网络的连通度为3的概率为0．321 4，如图3(b)所示。

(2)边界节点对网络连通度期望的影响

网络的连通度期望用于描述多次抛撒节点形成网络的连通度平均值，边界节点的存在使网络的连通度期望值减小，例如当n=100，存在边界节点的网络连通度期望值为1．590 8，而消除边界效应后的网络连通度期望值为3．770 5，如图4(a)所示。

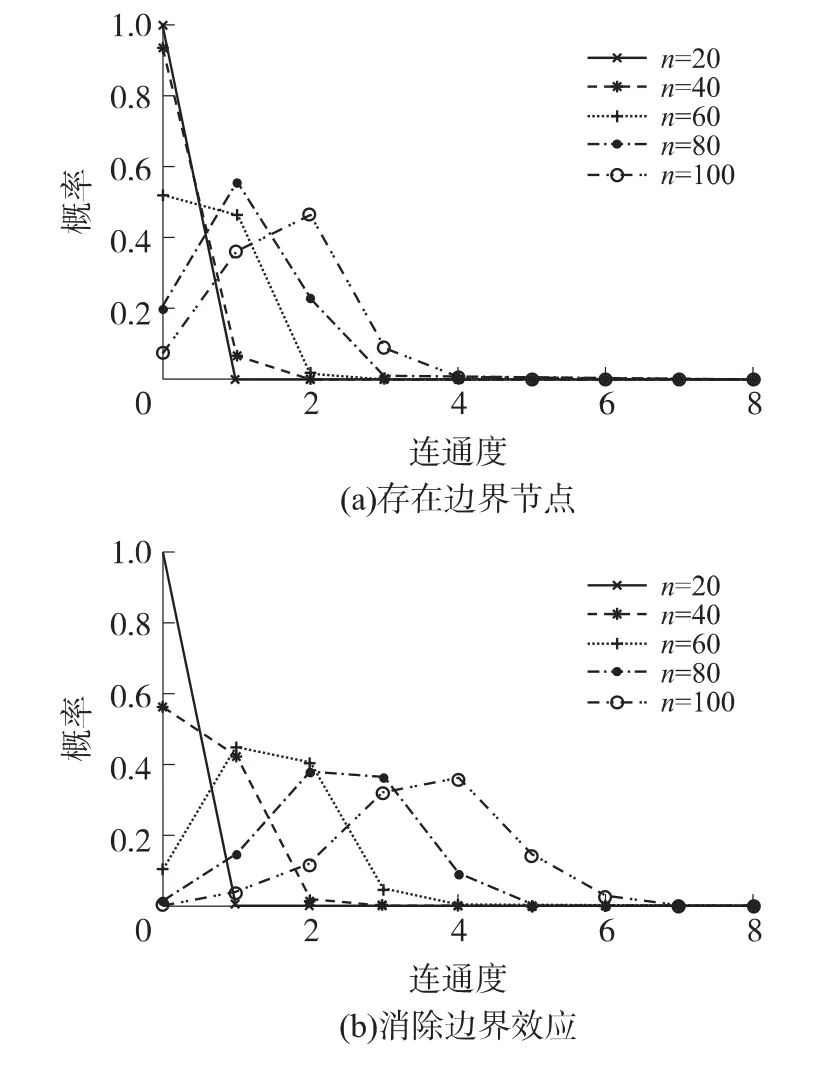
图3 网络的连通度分布

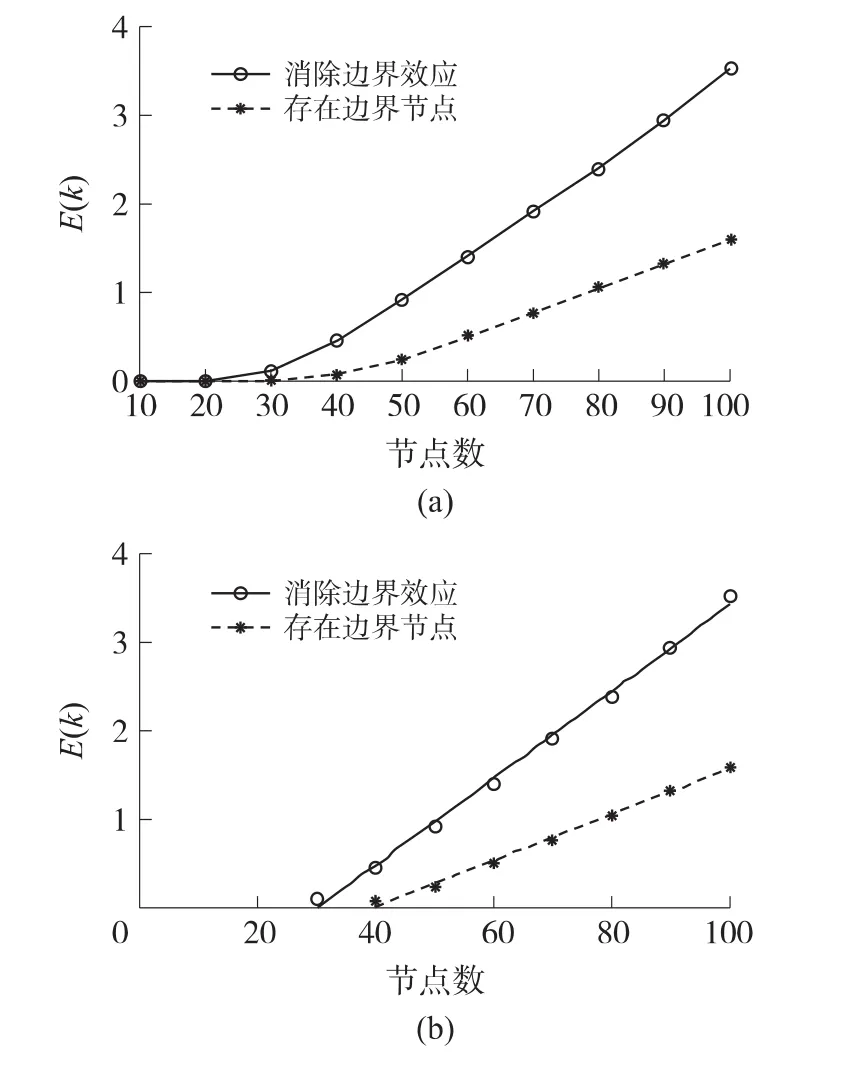
图4 网络的连通度期望及拟合曲线

随网络节点数增加，网络的连通度期望与节点数近似成线性关系(除去节点数较低时对应的非线性部分)，如图4(b)所示。本文对网络的连通度期望曲线进行了多项式拟合，当网络中存在边界节点时，得到下式:

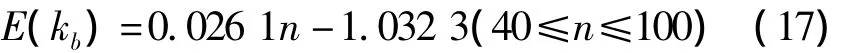
消除网络的边界效应，可得:

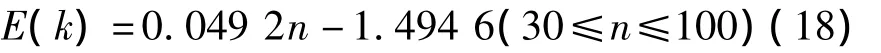
(3)边界节点对网络是k点连通概率的影响

“网络是k点连通的”指至少删除k个节点才能够是网络不连通，与“网络的连通度是k”概念不同。边界节点的存在使网络是k点连通的概率降低，如图5所示。以n=100为例，消除网络的边界效应，网络为 1、2、3 点连通的概率分别为:0．998 0，0．962 1，0．846 3;而边界节点的存在使网络为 1、2、3 点连通的概率降至:0．926 1，0．562 9，0．0958 。

图5 网络是k点连通的概率

式(16)给出了边界节点存在时，网络是k点连通的概率与网络最小度δ≥k的概率的近似对应关系。以n=100为例，网络为1点连通的概率为0．926 1，而网络的最小度 δ≥1 的概率为0．952 1，存在一定误差，随着网络节点数的增加，该误差将会减小。

4 结语

本文以节点的有效通讯面积为基础，对边界节点的连通性和网络的整体连通性进行了理论推导，得出边界节点有效通讯面积、边界节点邻居节点数的数学期望，以及边界节点存在的情况下，网络是k点连通的概率的近似表达式。而后通过仿真研究，进一步分析了存在边界节点与消除边界效应后的网络连通度分布、连通度期望以及网络是k点连通的概率，从而说明了边界节点对无线传感器网络连通性的影响，研究结果可用于指导无线传感器网络的连通性设计。

［1］ Bettstetter C，Krause O．On Border Effects in Modeling and Simulation of Wireless Ad Hoc Networks［C］//Proceedings of IEEE International Conferenceon Mobile and WirelessCommunication Networks(MWCN)．Recife，Brazil，2001:20 －27．

［2］ Bettstetter C．On the Connectivity of Ad Hoc Metworks［J］．Computer Journal，2004，47(4):432 －447．

［3］ Bettstetter C．On the Minimum Node Degree and Connectivity of a Wireless Multihop Network［C］//Proceedings of the International Symposium on Mobile Ad Hoc Networking and Computing(Mobi-Hoc)．Lausanne，Switzerland，2002:80 －91．

［4］ Bettstetter C，Klinglmayr J，Lettner S．On the Degree Distribution of k-Connected Random Networks［C］//Proceedings of 2010 IEEE International Conference on Communications，ICC 2010．Cape Town，South africa，2010．

［5］ Brust M R，Ribeiro C H C，Filho J A B．Border Effects in the Simulation of Ad Hoc and Sensor Networks［C］//Proceedings of 11th International Conference on Computer Modelling and Simulation．UKSim，2009:180－185．

［6］ Durvy M，Dousse O，Thiran P．Border Effects，Fairness，and Phase Transition in Large Wireless Networks［C］//Proceedings of IEEE INFOCOM．Phoenix，AZ，United states，2008:1274 －1282．

［7］ Jin Y，Jo J Y，Wang L，et al．ECCRA:An Energy-Efficient Coverage and Connectivity Preserving Routing Algorithm Under Border Effects in Wireless Sensor Networks［J］．Computer Communications，2008，31(10):2398 －2407．

［8］ Jin Y，Wang L，Jo J Y，et al．EECCR:An Energy-Efficient m-Coverage and n-Connectivity Routing Algorithm Under Border Effects in Heterogeneous Sensor Networks［J］．IEEE Transactions on Vehicular Technology，2009，58(3):1429 －1442．

［9］ Jin Y，Wang L，Yang X，et al．Analysis of Coverage Problem Under Border Effects in Wireless Sensor Networks［J］．High Technology Letters，2008，14(1):61 －66．

［10］ Wan P J，Yi C W．Coverage by Randomly Deployed Wireless Sensor Networks［J］．IEEE Transactions on Information Theory，2006，52(6):2658－2669．

［11］ Bollobás B．Random Graphs Second Edition［M］．Cambridge:Cambridge University Press，2001．

［12］张强，孙雨耕，房朝晖．无线传感器网络k点连通可靠性的研究［J］．传感技术学报，2005，18(3):439 －444．