基于 GIS的高质量约束Delaunay三角网格剖分

赵 晓 东,晏 小 宝,沈 永 明,王 亮

(1.大连大学院士创业园中日地层环境科学研究中心,辽宁大连 116622;2.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116023）

基于 GIS的高质量约束Delaunay三角网格剖分

赵 晓 东1,晏 小 宝1,沈 永 明2,王 亮2

(1.大连大学院士创业园中日地层环境科学研究中心,辽宁大连 116622;2.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116023）

在分析现有非结构化网格剖分算法的基础上,提出了一种 GIS支持下的改进分治算法实现约束Delaunay三角网格剖分。该方法利用了 GIS的空间拓扑关系对算法输入数据进行预处理,基于三角形的统一数据结构实现了网格细化,对输出剖分网格进行准确的拓扑和约束条件的检查,并基于推进阵面算法思想,结合空间邻近拓扑关系实现了三角剖分节点和网格的重新编号,方便了实际问题中开边界条件的赋值,提高了计算效率。实例应用表明,该方法大大简化了数值模型非结构化网格剖分的前处理过程,集成了几种综合算法的优点,在保证原分治算法时间复杂度的基础上,提高了约束条件下Delaunay三角网格生成的质量。

网格剖分;GIS;约束Delaunay三角剖分

0 引言

在应用有限元、有限差分和有限体积法对力学问题进行数值计算的前处理中,网格自动剖分占有重要的位置。目前,实现网格剖分的算法很多,而且不断有新的算法推出,其相关研究领域不仅针对数值模拟计算,对 GIS数据表达、地学分析、计算机视觉、表面目标重构等众多领域也是一项重要的应用技术[1-3]。网格剖分可分为结构化网格(Structured Grid）和非结构化网格(U nstructured Grid）两种。非结构化网格易于控制网格单元大小、形状及网格点位置,可以实现合理分布网格的密度,提高计算精度,因此具有比结构化网格更大的灵活性和对复杂边界更强的适应性。生成二维非结构化网格的常用方法[4]有四叉树法(Quadtree）、Delaunay三角剖分法(Delaunay Triangulation,DT）和推进阵面法(Advancing Front M ethod,A FM）以及几种方法的综合和改进。由于Delaunay三角网是Vo ronoi图的直线对偶图,具有空外接圆和最大最小角特性,还可以尽可能地避免病态三角形的出现,实现约束条件下的三角剖分,因此,在数值计算非结构化网格剖分和GIS三角网(TIN）的数据格式表达中广泛使用。

目前常见的构建Delaunay三角网的算法有:分治算法(Divide-and-conquer）、逐点插入算法(Incremental Insertion）、生长算法和扫描线算法(Sweepline）[3,5-7],其中以分治算法效率最高,时间复杂度为O(N logN）[5]。由于实际的不同需要,除几何约束条件外,对三角剖分的角度、大小和节点物理量的控制也都有相应约束,目前的剖分算法尚不能满足以上全部约束条件进行剖分。本文基于改进的分治算法,提供了梯度变化和针对实际问题的单元和节点重编号,并利用 GIS强大的空间数据处理和分析功能对算法做数据前后处理,保证了高质量约束Delaunay三角网格剖分的生成。

1 约束Delaunay三角化方法

分治算法[5]的基本思路是把输入点集分割为数个较小的点集,在各个子点集内生成小三角网,再逐级合并的一个递归过程。子点集最终只有两点或者三点,形成一条边、共线边或者三角形。算法必须将点集连接为凸区域(凸壳）,对凹区域和多连通区域会产生域外三角形,无法保证约束边的存在。约束Delaunay三角化的分治算法的关键过程及实现方法如下。

1.1 点集划分

原分治算法只有Y轴方向的分割,这里改进为交替分割[8],即点域X轴方向的长度大于Y轴方向的长度,则以X轴方向对半分割点集,否则以Y轴方向对半分割点集。该过程为递归调用的分割过程。

1.2 约束特征线重构

在Delaunay三角剖分上,采用逐次加入约束特征线的方法进行约束重构,可以证明该重构方法是收敛的[4],具体步骤如下:1）对于任一条约束直线,查找与之相交的三角形,即该约束线穿越的所有三角形组成的影响域;2）删除该影响域内的所有三角形,形成一个多边形空腔,称为恢复域;3）以该约束直线为界将恢复域一分为二,形成两个多边形子域;4）对这两个多边形子域进行Delaunay三角剖分,得到包含约束直线的影响域内的三角剖分;5）重复上述步骤,直至所有的约束线都被加入。

1.3 基于三角形的统一数据结构

Delaunay三角剖分涉及三角形和线段两类几何数据,如果将线段表示为退化的三角形势必增加算法特殊情况判断的冗余。如图1a所示,利用“影子”层表示完整的三角形结构,凸壳上的每一线段有一个顶点在无穷远处(算法中采用空指针）的“影子”三角形,特征线段有两个“影子”三角形。图1b中下端虚线三角形为子网合并中新建的“影子”三角形,阴影的三角形采用局部LOP优化算法[7],保证三角形的Delaunay特性。

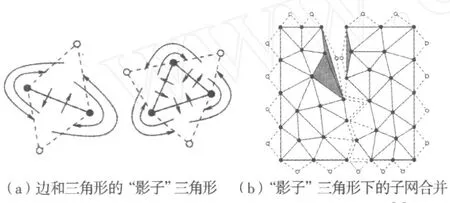
图1 分治算法的三角形数据结构和子网合并[9]Fig.1 Data structure of triangle and halfway through a merge step of the dividing and conquering algorithm

1.4 网格细化修正

剖分细化是在网格中插入顶点细化网格,使得网格最大和最小角满足约束。本文采用Shew chuk的细化算法[9,10],它是对 Ruppert和 Chew提出算法[11,12]的综合改进算法,顶点插入使用LOP算法[7],保证Delaunay特性,遵循两个规则:

规则1:一条线段的直径圆是唯一且最小的包含该线段的圆。如图2所示,如果有一点位于直径园内,则称该线段被侵入。任何被侵入线段在其中点位置插入顶点进行分割。

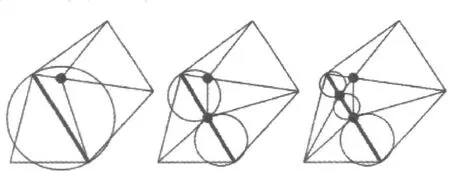
图2 线段被递归细分直至不被侵入为止[9]Fig.2 Segmentsare split recursively until no segmentsare encroached

规则2:一个三角形的外接圆是唯一经过三角形3个顶点的圆。如果三角形的一个角度过小或面积过大的情况下满足了约束条件,则称该三角形为坏三角形。如图3所示,以外心顶点(外接圆的中心）作为插入点进行分割。

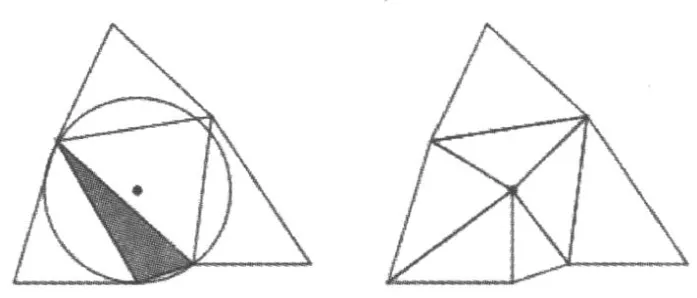
图3 每个坏三角形线在外心顶点插入分割[9]Fig.3 Each bad triangle is split by inserting a vertex at its circumcenter

剖分细化具体算法如下:1）取约束线段集合中的每一条约束线段,检查它是否被其他点侵入,是则转第2步;否则转第3步。2）按规则1将约束线段分割,将新的约束线段加入约束线段集合,转第1步。3）取剖分三角形集合的三角形进行检查,全部合格,转第5步;否则,对于不满足约束条件的三角形按规则2插入点。4）如果插入点不侵入约束线段,将该点插入网格中,转第3步;否则,转第2步。5）算法收敛停止。

2 GIS支持下约束Delaunay三角网格剖分

高质量Delaunay三角网格意味着必须满足一定的约束条件,而约束条件是根据工程需要或者数值模拟的条件给定的,如流体动力学问题一般在边界、结构物和扩散源附近采取网格加密方法,这些都要对输入点集进行预处理;输出的剖分三角形内角不能太大也不能太小,面积梯度变化适中。因此,要实现本文提出的非结构网格生成算法,需要提取计算区域边界点的坐标,包括外边界和内边界上各节点光滑、间距的处理、内部约束特征线的设置等。如图4所示,这些预处理都可以在 GIS的支持下完成,同时可以实现空间数据的管理,保证数据的拓扑准确性和剖分三角网格的正确性。

2.1 边界点的输入

剖分算法输入的为点集的坐标值,非实际的拓扑数据,而且边界点组织直接影响到剖分输出的结果,需要在输入前进行必要的预处理。如图4所示,按照拓扑关系,将输入数据划分为Polygon、Polyline和Point 3种矢量数据,其涵盖了流体动力学问题中的海岸边界、岛屿、开边界和水深等高线等所有输入数据。其中,海岸边界采用Douglas-Peucker算法做简化处理后,根据实际计算需要,对边界和岛屿边界线上节点进行光滑处理。

图4 GIS下Delaunay三角化网格剖分流程Fig.4 Flow diagram illustrating Delaunary triangulation mesh generation in GIS

2.2 Delaunay三角网格剖分

采用本文改进的分治算法实现约束Delaunay三角网格剖分,并将算法集成在A rcGIS平台中。如图5所示,直接输入经过预处理的边界控制线Polyline、边界控制区域 Polygon和控制点 Point,可直接输出Delaunay三角网格剖分网格及节点。

2.3 三角剖分网格拓扑检查及编辑

如果初始输入的约束之间没有形成尖锐角度,算法能够生成最小角度30°的Delaunay剖分网格,并具有较好的梯度。但在初始约束不当和特殊约束条件下,算法还不能保证满足所有约束条件,因此对算法生成的剖分三角形的拓扑检查是必要的。如图6所示,对局部没有满足约束条件的三角网格,可通过GIS下的拓扑编辑修正节点以满足其约束条件。

2.4 剖分三角节点及网格的重编号

图5 GIS下的Delaunay三角网格剖分Fig.5 Delaunay triangulation mesh generation in GIS

图6 三角剖分网格拓扑检查Fig.6 Topological check on triangulation meshes

算法生成的Delaunay三角网格是没有规律的,给实际数值模拟带来不便,如水动数值模型的边界条件是从开边界开始设定的,因此需要对剖分网格节点及网格重新编号。这样不仅可以和数值模型开边界的编号完全耦合,还使得相邻网格之间和相邻节点间的编号跨度减小,从而减少计算中调用各网格信息的时间花费,提高计算效率。重编号算法采用AFM法的思想,以开边界为起始边界,按照空间邻接关系向前推进,直到遍历所有剖分节点,具体步骤如下[13]:1）如图7所示,给定起始边界线(这里为开边界线）、三角剖分 Polygon和剖分节点 Point数据,设定排序方法;2）根据起始边界线空间检索与之相交的节点Point,检索结果按照设定方法排序;3）根据检索到的节点Point空间检索与之相交的三角剖分Polygon,以其中心点为基点对未排序三角剖分Polygon按照设定方法排序;4）根据检索到的三角剖分Polygon空间检索与之相交剖分节点Point,判断是否有未排序节点,如果没有,算法结束,否则,按照设定方法排序后返回第3步,直到算法收敛。

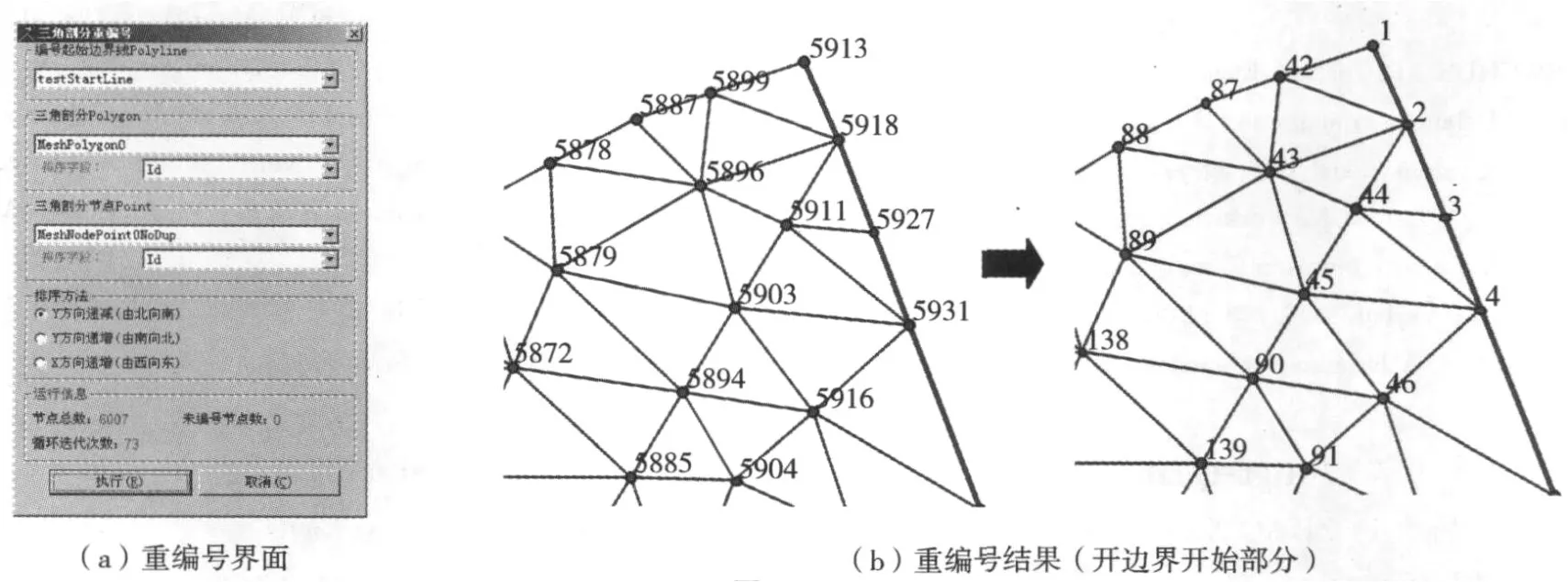
图7 三角剖分网格重编号Fig.7 Re-numbering of triangulation meshes

3 算例及应用

采用本文算法分别使用随机离散点集和实例计算海域进行了测试和应用,测试硬件为 Intel Co re Duo CPU 1.8 GHz,内存2 GB,操作系统 W indow s XP SP3,算法时间不包括输入/输出时间。

表1为几种主要算法在随机离散点集下的测试结果,从时间复杂度看,改进的分治算法基本与原分治算法保持一致,在使用了“影子”三角形的统一数据结构下,时间上明显优于其他几种传统算法。本文提出的算法在保持原分治算法时间复杂度的前提下,满足了约束条件以适应实际问题计算的要求,其结果令人满意。表2为日本博多湾(图8）和中国渤海区域的海洋数值模拟中的应用算例,Delaunay三角剖分能很好地满足特征约束,计算速度快,能满足水动数值模拟非结构网格的计算要求。

表1 随机离散点集算例Table 1 Examples using random points s

表2 应用算例计算输入参数及输出结果Table 2 Input parametersand output results of examples in case study

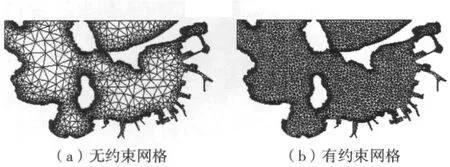
图8 日本博多湾Delaunay三角剖分Fig.8 Delaunay triangulation of Hakata Bay,Japan

4 结语

本文在 GIS平台下基于改进的分治算法实现了高质量约束Delaunay三角网格剖分,改进的分治算法保持了原算法的时间复杂度,并利用 GIS空间数据处理功能完成了数据输入和输出剖分网格的准确拓扑检查,提高了非结构化网格的质量和准确度;同时针对实际问题的需要,基于推进阵面算法的思想,结合空间邻近拓扑关系实现了三角剖分节点和网格的重新编号算法。算例测试和实例应用表明,本文提出的方法集成了几种综合算法的优点,算法收敛速度快,网格生成质量高,满足实际问题的约束条件,应用效果较好。

[1] 芮一康,王结臣.Delaunay三角形构网的分治扫描线算法[J].测绘学报,2007,36(3）:358-362.

[2] 胡金星,马照亭,吴焕萍,等.基于网格划分的海量数据Delaunay三角剖分[J].测绘学报,2004,33(2）:163-167.

[3] 武晓波,王世新,肖春生.Delaunay三角网的生成算法研究[J].测绘学报,1999,28(1）:28-35.

[4] 王盛玺,宋松和,邹正平.基于约束Delaunay三角化的二维非结构网格生成方法[J].计算物理,2009,26(3）:335-348.

[5] LEED T,SCHACHTER B J.Two algorithms for constructing a Delaunay triangulation[J].Computer and Information Sciences,1980,9(3）:219-242.

[6] FORTUNE S.A sweepline algorithm for VoronoiDiagrams[J].Algorithmica,1987,2(2）:153-174.

[7] LAWSON C L.Software for C1 surface interpolation[A].RICE J R.Mathematical Software III[C].New York:Academic Press,1977.161-194.

[8] DW YER R A.A Faster divide-and-conquer algorithm for constructing Delaunay triangulations[J].Algorithmica,1987,2(2）:137-151.

[9] SHEWCHU K J R.Delaunay refinement algo rithm s fo r triangular mesh generation[J].Computational Geometry,2002,22(1-3）:21-74.

[10] SHEWCHUK JR.Triangle:Engineering a 2D qualitymesh generator and Delaunay triangulator[A].L IN M C,MANOCHA D.Applied Computational Geometry:Towards Geometric Engineering[C].First ACM Workshop on Applied Computational Geometry,Lecture Notes in Computer Science,Vol.1148.Berlin:Springer-Verlag,1996.203-222.

[11] RUPPERT J.A Delaunay refinement algorithm for quality 2-dimensionalmesh generation[J].A lgorithms,1995,18(3）:548-585.

[12] CHEW L P.Guaranteed-quality mesh generation for curved surfaces[A].Proceedings of the Ninth Annual ACM Symposium on Computational Geometry[C].San Diego,CA:ACM Press,1993.274-280.

[13] 赵晓东,王海龙,沈永明.基于 GIS的二维非结构化剖分网格优化[J].地理与地理信息科学,2010,26(2）:46-48.

High-Quality Constrained Delaunay Triangulation Based on GIS

ZHAO Xiao-dong1,YAN Xiao-bao1,SHEN Yong-ming2,WANG Liang2
(1.China-JapanResearchCenterforGeo-environmentalScience,PioneerParkofAcademician,DalianUniversity,Dalian 116622;2.StateKeyLaboratoryofCoastalandOffshore Engineering,DalianUniversityofTechnology,Dalian116023,China）

The unstructured mesh generation isoneof the key technical issues in many fields such asmechanical computation and numerical simulation.Based on the analysis of existing unstructured mesh generation algo rithms,the imp roved divide-and-conquer algo rithm suppo rted by GIS isp roposed to dealwith constrained Delaunay triangulation.Thismethod makes useof the GIS spatial topological relations to handle the p re-p rocessing of input algo rithm data,imp lements Delaunay refinement using a triangle-based data structure,and checks the output meshes with accurate topology and constraints.Based on the idea of advancing f ront algo rithm and spatial topological relations between the mesh nodes and triangulation,the re-numbering algo rithm is also p roposed to facilitate the assignment of theopen boundary conditionsaswell as imp roving the computational efficiency.The app lication to the p ractical simulation show s that the p roposed method can simp lify numerical model p re-p rocessing of unstructured mesh generation,p reserve the advantages of several algorithm s w ith the original running time,and imp rove the quality of constrained Delaunay triangulations.

mesh generation;GIS;constrained Delaunay triangulation

P208

A

1672-0504(2010）05-0024-05

2010-04- 21;

2010-06-10

国家自然科学基金重点项目(50839001）;国家自然科学基金项目(50874021、50779006）;辽宁省高等学校科研项目计划(L20100321）

赵晓东(1969-）,男,博士,教授,从事 GIS在采矿、岩土工程应用和水动模型耦合的研究。E-mail:xdong.zhao@gmail.com