基于VC 的七参数坐标转换模型研究及实现

闫 庆 庆,王 宝 山,訾 国 杰

(河南理工大学测绘与国土信息工程学院,河南焦作 454000）

闫 庆 庆,王 宝 山,訾 国 杰

(河南理工大学测绘与国土信息工程学院,河南焦作 454000）

我国法定的国家大地坐标系为北京54坐标系和西安80坐标系,北京54坐标系采用的参考椭球为克拉索夫斯基椭球体,而西安80坐标系采用的参考椭球为 IAG75椭球体[1]。目前国家基础测绘及一些工程项目普遍采用西安80坐标系,在进行控制测量时必将涉及54坐标系与80坐标系之间的转换问题。宗刚军等[2]对坐标转换算法做了相关研究。本文在分析七参数Bursa-Wolf转换模型的基础上,利用QR分解法解决了矩阵求逆过程中出现的数值不稳定问题,并基于VC实现了两种坐标系统间的转换问题。根据兖矿发耳矿井测量点,对部分 GPS网控制点进行54坐标与80坐标的计算转换试验。该模型简单、方便、可行,具有一定的实用意义。

1 坐标转换求解模型

在大地测量坐标转换中,广泛使用七参数Bursa-Wolf转换模型[3]解决54坐标系至80坐标系的转换问题,其模型为:

在具体转换时先选用至少3组重合点(X54,Y54,Z54）和(X80,Y80,Z80）,采用最小二乘法解算出方程中的转换参数,然后利用上述方程式实现其他数据的统一转换。

2 QR矩阵分解法

在用最小二乘法求解转换参数时涉及矩阵的求逆运算,以式(3）为例,其误差方程的系数阵A为N＊7阶,其中N为公共点数目。利用最小二乘法时需要求ATBA的逆矩阵,也即求一个7＊7阶矩阵的逆矩阵,并且对于坐标转换而言,坐标数据一般较大,因此很容易导致求逆的数值不稳定。一种合理的解决方法是采用QR分解法[4],将系数矩阵A分解为:

其中:Q为N＊7的列正交矩阵,R为7＊7的上三角矩阵,由于Q正交,QTQ=I,所以式(3）变为:

这样通过上式无需通过矩阵求逆即可得到转换参数S的最小二乘解。

3 算法实现

3.1 定义坐标系结构体及转换参数结构体

3.2 七参数坐标转换算法

在已知某一矿区北京54坐标系大地测量点坐标情况下,根据坐标转换参数,可计算相应的西安80坐标系坐标数据。针对矩阵表达式(3）用最小二乘法解算出其中的转换参数,具体实现过程如下:1）输入一组54坐标到坐标数组co54A rr和一组80坐标到坐标数组co80A rr;2）把矩阵A分解成Q矩阵和R矩阵;3）根据式(7）计算出坐标换算参数(七参数）:3个平移参数X0、Y0、Z0,3个旋转参数ωx、ωy、ωz和 1个尺度参数k。4）把计算后的参数代入式(3）,计算相应的80坐标系的空间直角坐标X80、Y80、Z80。

在用最小二乘法求解未知的测量点数据时,利用QR矩阵分解可避免矩阵求逆过程中出现的不稳定性,使求得的测量点数据与实际数据之间误差的绝对值之和最小,从而提高54坐标向80坐标的转换精度。

4 实例分析

利用兖矿发耳矿井的实际测量点坐标数据对程序进行验证,从10个测量点中选取3个同名点参与坐标转换参数的计算。相应的坐标数据见表1。

表1 发耳矿井测量点数据

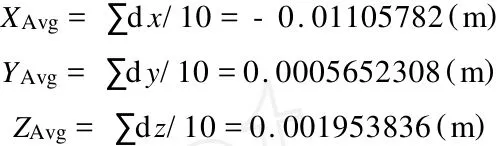
把计算得到的坐标转换参数代入式(2）,输入该矿区测量点的北京54坐标,得到的西安80坐标及误差见表2。

表2 发耳矿井测量点坐标转换精度

5 结论

本文考虑Bursa-Wolf转换模型中7个转换参数对大地直角坐标系中坐标转换精度的影响。通过表2可看出,转换点位误差最大为1.6 cm,最小为0.1 cm。该数学模型简单,适于计算机编程解算,借助常规数字成图软件,如LongRuan GIS可以实现较大区域范围内新、旧坐标之间的快速转换,在控制点本身测量精度较高的条件下,坐标换算误差很小,可满足矿区测量要求。

[1] 彭爱文,曹佩瑶.平面坐标转换方法探讨及转换软件的设计思路[J].测绘与空间地理信息,2007,30(3）:189-191.

[2] 宗刚军,姚顽强.工程测量新旧坐标转换的一种实现方法[J].西安科技大学学报,2007,27(3）:401-404.

[3] 朱华统.大地坐标系的建立[M].北京:测绘出版社,1986.

[4] 陈兆林,张书华,闵珊.两种坐标转换模型的精度比较[J].四川测绘,2007,30(5）:224-227.

河南省科技攻关资助项目(0524220343）

闫庆庆(1984-）,女,硕士研究生,研究方向为地理信息服务。E-mail:yanqingqing1213@163.com