球面元胞自动机框架的比较与选择

肖志峰,翟晓芳

(武汉大学测绘遥感信息工程国家重点实验室,湖北武汉 430079）

球面元胞自动机框架的比较与选择

肖志峰,翟晓芳

(武汉大学测绘遥感信息工程国家重点实验室,湖北武汉 430079）

在球面构建基本的元胞自动机框架是球面元胞自动机研究的基础。该文从球面空间特性出发,分析比较了四边形、三角形和六边形网格的不同几何特性和元胞运动机制,提出了基于六边形网格的元胞自动机框架模型,描述了其基本定义、运动机制和坐标系统,并构建了球面六边形元胞自动机原型系统进行模拟实验,结果表明,该元胞自动机框架能有效支持球面元胞自动机的深入研究。

球面;元胞自动机;六边形

元胞自动机是离散动力学系统[1,2],元胞自动机研究常集中在元胞自动机的演化规则上。随着生态系统模拟、气候模拟、环境模拟等研究的发展[3],在球面或椭球面上研究元胞自动机的演化日益成为热点。球面空间是一个各向异性的复杂的流形,它属于非欧空间,在球面空间上无法完全建立与平面空间的一一对应关系,不能完全照搬平面空间上的相关研究成果[4]。因此,球面元胞自动机研究在元胞网格选择、运动机制、编码规则及多尺度分析等方面与平面空间的元胞自动机都存在差异,必须从球面元胞网格的空间特性和球面空间拓扑特性出发,发展适用于球面的元胞自动机框架。

1 球面元胞网格的选取

元胞自动机研究的基础在于元胞网格的选取,不同的元胞网格有不同的空间特性,绝大多数元胞自动机网格都是四边形,由于球面空间是黎曼空间,四边形网格在球面空间无法实现完全覆盖。元胞网格在参考空间的位置、大小和面积均能不同程度影响元胞自动机演化的效果,因此,以球面为参考空间的元胞自动机网格的选取也有别于平面空间。本文提出了球面元胞网格选择的5点要求:1）元胞网格的分布方式相同,大小和形状相同,地位平等,空间分布规则整齐[5];2）各个元胞网格在每个时刻的状态变化是独立的行为,相互没有任何影响;3）元胞网格应完全覆盖全球,无重叠和遗漏;4）元胞网格具有相同的面积和形状;5）每个元胞网格只有一个网格参考点。

球面元胞自动机网格与离散全球网格系统(DGGs）[6,7]存在很大的类比性。DGGs是一种新型的地理空间网格结构,它由规则的多边形构成,目前存在三种规则多边形进行空间覆盖而无任何缝隙,即三角形、四边形和六边形(图1）,其他多边形进行空间覆盖则会产生邻近像素不等距、覆盖缝隙或重叠。

图1 三角形、四边形、六边形球面网格Fig.1 Spherical grids of triangle,square and hexagon

四边形网格是构建平面网格的常用单元形状,在球面上以等角的经纬度网格最为流行,等角经纬度网格有大量优点,它基于二维笛卡尔坐标系统,已被广泛应用。经纬度网格系统目前已经成为众多空间数据管理、处理软件的基础。四边形网格边界并不一致,每个四边形网格单元有四个共享边的邻近网格,其中心距离与网格中心等距。同时,每个网格有四个共享顶点的邻近网格,但这些网格的中心点距离大于共享边网格的中心点距离,显示出各向异性的特点。因此,每种邻近网格对中心网格的贡献程度也不同,而大多数基于四边形的元胞自动机研究认为边邻近网格和角邻近网格对中心网格的贡献一致。

经纬度网格系统存在的另一个重要缺陷就是当网格从赤道地区向高纬度地区移动时,其形状和面积变形均显著增大。在南极和北极点,网格变成三角形(在其他地区为矩形）。这对于具有同质性和齐性的元胞空间难以接受。很多学者提出了不同的改进方法,如减少单元的数量、增加纬度,使之获得了一致的单元格大小,或采用纬线或经线方向单元格边界的相似变换使网格近似等面积。但这些成果在获得等面积的同时,都使单元格形状越来越不规则且单元格接边更复杂。

三角形网格避免了四边形网格在赤道和两极出现的较大面积差异,以基于三角形网格的QTM系统为例,其最大与最小网格的面积比约为1.8[8];同时三角形网格拥有较少的邻居数目,它与正方形网格都是不一致邻近,每个单元有3个边邻居和9个节点邻居;其次,三角形网格覆盖单元不具有一致的定向,如图2,一些三角形朝上,一些三角形朝下,难以符合元胞的齐性规则,对这种特殊情况需要额外考虑[8]。

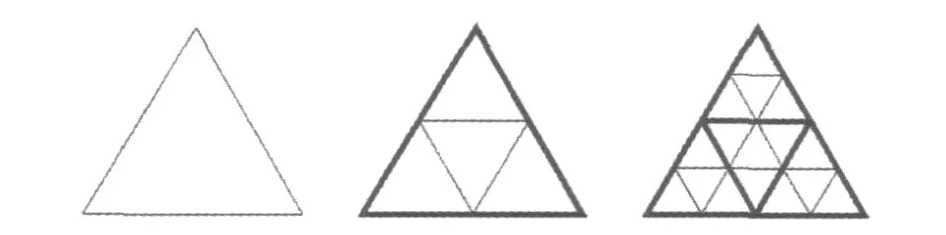
图2 三角形网格Fig.2 Grids of triangles

六边形网格是空间最紧凑的网格[9],其拥有最大的角分辨率。与三角形和正方形网格不同,六边形具有一致邻近的特性:每个六边形单元有六个共享边的邻近单元,其邻近单元的中心点与中心网格的中心点距离相等。每个六边形网格没有共有一个顶点的邻近单元,这一特性使六边形在离散空间仿真中受到更多重视,六边形网格的六个离散速度矢量足够用来模拟连续的、各向同性的流动量。在球面空间中,六边形不能完全覆盖整个球面,使用六边形进行球面空间划分时,在所有柏拉图多面体的顶点处都会出现一个非六边形的多边形,这种多边形的个数与多面体的顶点数相关,与网格的分辨率无关,在采用二十面体的六边形网格中,共有12个五边形。由于五边形的数量是固定的,相对元胞网格的总数量非常少。同时还可采用一定的处理模型来削弱五边形网格对空间结构和元胞演化的影响,因此五边形的存在不会影响球面元胞自动机的模拟效果[10]。

2 球面元胞网格的邻域比较

元胞自动机模型中的元胞个体通常不可移动,元胞自动机在整体上的运动通过元胞个体的状态变化实现。状态的变化除受转换规则影响外,还受元胞所在邻域的影响,而不同的元胞网格对邻域的影响机制也不完全一致。根据元胞网格的邻近位置不同区分为两类领域:直角邻域和对角邻域。直角邻域共享一条边,对角邻域共享一个角,对角点通常被作为元胞运动的障碍点,所以对角邻域对元胞的状态无影响。在不同的应用中,对元胞的邻域要求也不一样,冯-诺依曼(Von.Neumann）邻域和摩尔(Moore）邻域是最主要的领域规则,冯-诺依曼邻域为共享边的直角邻域,摩尔邻域则既包括直角邻域也包括对角邻域,并认为对角邻域和直角邻域对元胞的影响相当。

四边形元胞网格的冯-诺依曼邻域(图3a）为一个元胞的上、下、左、右相邻四个元胞。这里,邻域半径r为1,相当于图像处理中的四邻域、四方向。摩尔邻域(图3b）是指一个元胞的上、下、左、右、左上、右上、右下、左下相邻的八个元胞。邻域半径r同样为1,相当于图像处理中的八邻域、八方向。

图3 四边形元胞的邻域Fig.3 Neighborhood of square CA

三角形元胞网格的冯-诺依曼邻域为一个元胞的上、左、右(图 4a）或下、左、右(图 4b）的相邻三个元胞。摩尔邻域(图4c）是指一个三角形元胞的所有直角和对角邻域。从图中可以看出,三角形元胞的某些对角邻域已经远离中心元胞,难以受到中心元胞的影响,缺少实际意义。

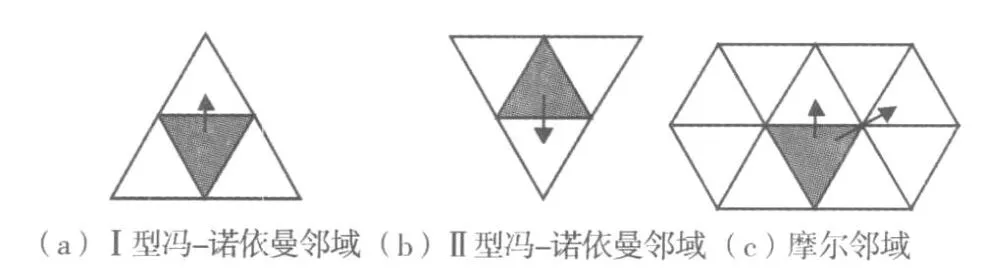
图4 三角形元胞的邻域Fig.4 Neighborhood of triangle CA

六边形网格的邻域规则最为简单,其只有6个邻居,每个邻近网格都拥有一个公共边和两个公共顶点(图5）,即不用考虑复杂的邻接情况,且各方向的运动机制完全一致[3]。这种简化的设计导致六边形网格拥有更加简易和高效的算法,并且由于六边形网格邻域可以定义更多流向,与现实情况更加接近。

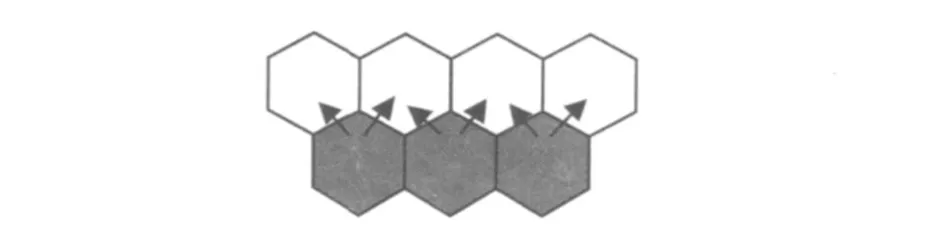
图5 六边形元胞的邻域Fig.5 Neighborhood of hexagon CA

3 基于六边形网格的球面元胞自动机框架

3.1 基本定义

3.2 元胞网格坐标系统

球面空间众多的元胞网格需要置于统一的坐标系统才能进行各种演化运算。六边形网格与四边形网格不同,六边形网格的点不能对齐相互垂直的两个方向,同时球面空间的拓扑关系也不同于平面空间的拓扑关系,因此不能直接使用传统的笛卡尔坐标系统表示六边形网格点位。

从元胞自动机演化的简化性考虑,可使用与笛卡儿坐标系统类似的二轴坐标系统,称为二轴倾斜坐标系统或h2坐标系统,它是使用与六边形对称轴方向相一致的一对倾斜轴,一个六边形网格可使用一对整数坐标值来表示。倾斜坐标系统有几种不同的变体(图6）,其坐标轴分别相距120°或60°。

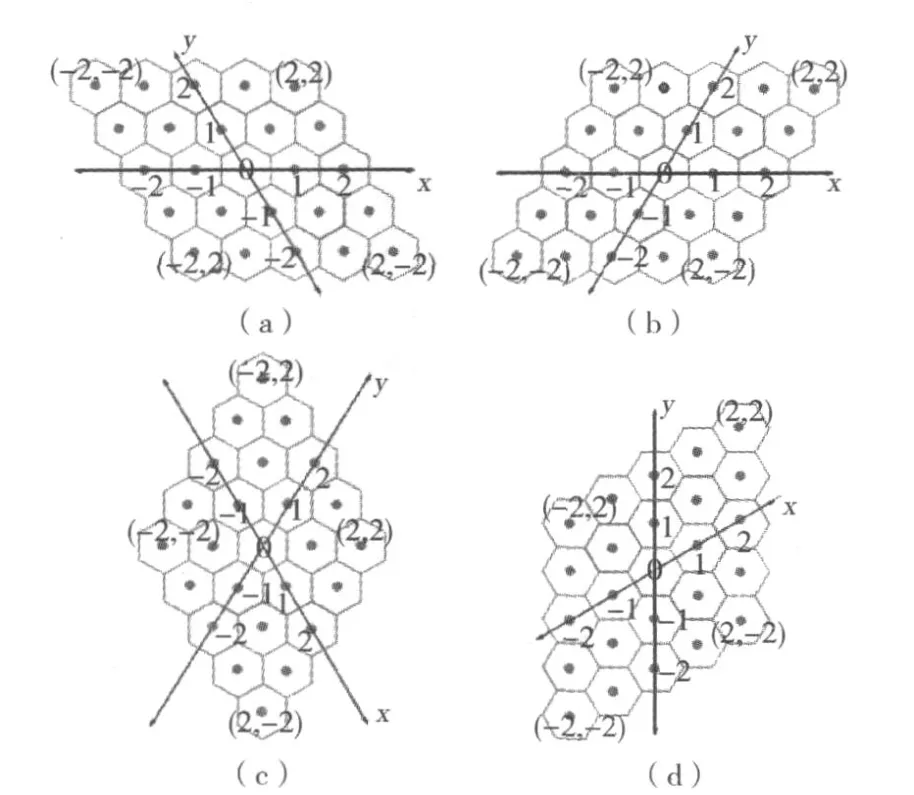
图6 六边形网格的二轴倾斜坐标系统Fig.6 2-Axis slope coordinate system of hexagon grids

二轴倾斜坐标系统具有明显的特性:1）完整性:能够表示二维空间中的任何六边形网格;2）唯一性:任何不同的坐标对只对应唯一的网格;3）可转换性:能够简单地与笛卡尔坐标系进行相互转换;4）高效性:方便而有效。由于二轴倾斜坐标系统并不能完整覆盖整个球面,一般将球面剖分为多个子域,在每个子域构建局部的二轴倾斜坐标系统。Sahr在二十面体网格中将整个球面划分为10个子域[11],每个子域由9个或10个初始六边形构成,通过进一步划分可以得到更高分辨率的六边形网格。因此,在全球元胞自动机网格中,每个网格的地址由该网格所在的四边形子域加上该子域内倾斜坐标来表达,如{0,2,1}表示在第一个四边形子域内第二行、第一列的网格。对于每个四边形子域,都可以使用一个二轴倾斜坐标系统来表达(图7）。

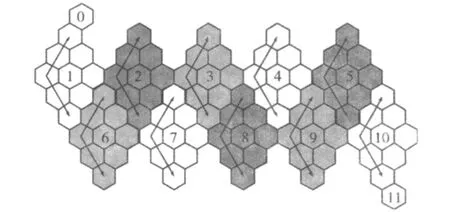
图7 全球二十面体的二轴倾斜坐标子域Fig.7 Sub-area of 2-axis slope coordinate system of icosahedrons in sphere

4 球面元胞自动机框架实验

为了验证基于球面的元胞自动机框架,本文使用三维可视化引擎Wo rldW ind构建球面元胞自动机原型,主要用来验证球面元胞自动机的网格剖分、网格编码与元胞运行机制。球面元胞自动机原型采用JOGL作为三维渲染引擎,在java版WorldWind的基础上进行开发,实现了全球和局部的六边形元胞自动机网格生成与基本扩展机制。

虽然球面元胞自动机框架主要在全球范围内应用,但局部区域内的元胞自动机模拟也可以使用球面元胞自动机框架,图8是湖北省的元胞自动机网格模拟,图9是2002年武汉市土地利用图的元胞自动机网格图。

本文对2002年、2005年等多个时间的武汉市土地利用遥感影像图进行解译,在构建的球面元胞自动机框架上使用逻辑回归模型对武汉市土地利用现状进行演化运算,采用逐点对比和整体比较的方法对模拟结果进行比较。实验表明,基于六边形网格的元胞自动机模拟更适宜于不确定方向的扩展,在土地利用现状的变化趋势方面更加符合实际情况,能满足针对全球变化的仿真模拟应用。

5 结语

随着研究区域扩展到全球范围,基于四边形网格的元胞自动机研究出现了一些不适应的情况,由于球面空间的特殊性,在球面上构建元胞自动机更需考虑元胞网格面积变形、邻接关系等方面,本文提出的球面元胞自动机框架采用六边形作为元胞网格的基本形状,在面积一致性和拓扑邻接一致性等方面均优于四边形和三角形网格,由于六边形的演化规则与四边形有较大差异,因此在演化算法上仍需

进行更多研究。

[1] 黎夏,叶嘉安.地理模拟系统:元胞自动机与多智能体[M].北京:科学出版社,2007.

[2] 周成虎,孙战利,谢一春.地理元胞自动机研究[M].北京:科学出版社,1999.

[3] ROSS K A,SAHR K.Planar and spherical hierarchical,multiresolution cellular automata[J].Computers,Environment and U rban Systems,2008,32:204-213.

[4] EGENHOFER M J.Spherical topological relations[J].Data Semantics III,2005(LNCS 3534）:25-49.

[5] GOODCH ILD M F.Geographical grid models for environmental monitoring and analysis across the globe[A].Proceedings of GIS/L IS′94 Conference[C].1994.

[6] SAHR K,WH ITED.Geodesic discrete global grid systems[J].Cartography and Geographic Information Science,1998,30(2）:121-134.

[7] GOODCH ILD M,YANG S R.Tessellation of the sphere[R].NCGIS Spatial Analysis on the Sphere——A Review Technical Repo rt,1994.94-97.

[8] DU TTON G.Encoding and handling geospatial data with hierarchical triangular meshes[A].Proceeding of 7th International Symposium on Spatial Data Handling,1996.34-43.

[9] M IDDLETON,LEE,SIVASWAM Y,et al.Hexagonal image p rocessing:A p ractical app roach[R].Sp ringer,2005.16.

[10] HA IX F.Research on the comparison of extension mechanism of cellular automaton based on hexagon grid and rectangular grid[A].p roc.of SPIE vol.7492 74924K-1[C].2009.

[11] SAHR K.Location coding on icosahedral aperture 3 hexagon discrete global grids[J].Computers,Environment and U rban Systems,2008,32(3）:174-187.

Com par ison and Selection of Cellular Automation Framework on Sphere

XIAO Zhi-feng,ZHA IXiao-fang
(LIESMARS,WuhanUniversity,Wuhan430079,China）

With the rapid development of global change research,the evolution simulation of cellular automaton in spherical space has been taken mo re seriously.Constructing the basal cellular automaton framewo rk is the basement of research of spherical cellular automaton.This paper started from the spherical spatial characteristics.And the quadrangle grid′s,triangle grid′s and hexagon grid′s different geometric p roperties and cellular movementmechanism were analyzed and compared,then the cellular automaton framework model based hexagon grid was put fo rward,its basic definition,movement mechanism and reference frame were described,and a spherical hexagon cellular automaton antetype system was built to do simulation experiment.The result showed that this cellular automaton f rame can suppo rt the in-dep th study on spherical cellular automaton effectively.

sphere;Cellular Automation;hexagon

P208

A

1672-0504(2010）05-0007-04

2010-05- 17;

2010-06-11

国家重大基础研究项目(61399）

肖志峰(1977-）,男,博士,讲师,主要研究空间信息网格与高性能空间信息服务。E-mail:xiaozf@gmail.com