基于GNSS的通信星座系统的时间同步研究

黄 琳 马文杰 李国军 霍德聪 蒙 薇 杨 芳

(航天东方红卫星有限公司,北京 100094)

1 引言

2 基于GNSS的通信卫星星座系统时统技术方案

全网时间同步技术是卫星星座系统的核心技术之一。就同步内容而言,对不同时钟的秒脉冲相位差进行调整是一个物理过程,称为物理同步;若不进行相位差调整,而只是广播相位差以使有关部分进行同步则是一个数学过程,称为数学同步。物理同步和数学同步构成了时间同步的两大基本内容[1]。与导航星座系统重点关注星间数学同步[2-3]的情况不同,本文更关注通信卫星星座系统的空间段与地面段的时间同步问题,即,各星上时钟与地面系统时钟的秒脉冲相位同步。

当前,国外著名的通信卫星星座系统的星地时间同步处理,基本上都依赖全球布设的地面站系统来完成。比如,具有星间链路的铱星(Iridium)系统有11个全球分布的地面站;不具有星间链路的全球星(Globalstar)系统需要300 多个地面站。然而,由于我国地面站的分布区域有限,地面站只能在卫星过境的短时期内观测到星地时差,为了实现高精度同步,必然对硬件性能(比如,时钟)和星地时差预报模型的估计精度提出过高要求,从而导致星座系统总成本和工程实现的困难程度大大上升。显然,这种以地面站介入控制为主的时统方法不太适合我国的星座系统的星地时间同步处理。

为了提高星座系统时统操作的可靠性,且考虑到当前绝大多数卫星都装备某种全球导航卫星系统(GNSS)(比如GPS 或GLONASS)接收机,因此,基于GNSS系统实现星座系统的时间同步是一个可能选择。比如,G PS系统作为一个高精度、高稳定度时间基准,已成功用于相距数千千米之遥的地面站间时钟同步[4]。本文将引入星上时间管理单元自主完成星地时统处理的思想,提出一个基于GNSS系统实现近地全球通信卫星星座系统全网星地同步的技术方案,重点设计一个半实物仿真方案,并利用数学、半物理仿真对该技术方案的正确性与可行性进行了验证。

2.1 方案概述与时统关键技术

时统方案主要内容包括:地面站和各星座星上的GNSS 接收机每隔一定周期测得地面系统时钟、各星上时钟相对于GNSS系统时钟的相位差。而地面系统时钟相对GNSS系统时钟的时差观测量经过星地、星间链路,被发送给任一星上时间管理单元,并与各星座星上测得的时差量一起进行折算,得到各星时钟相对地面系统时钟的时差观测量。各星上时间管理单元中的卡尔曼滤波器(KF),周期性估计出星地时差预报模型中的几个变量(时差量、频差和频漂率)、并周期性利用新估计结果替换掉时差预报模型的原有变量估计。同时,时间管理单元基于星上时差预报模型进行时差广播,并进行自主调相时机的判断,若调相时机到来,则自动发出指令驱动秒脉冲发生器进行相应相位差的调整,从而将各星上时钟相对地面系统时钟的秒脉冲相位差控制在同步指标要求的范围内。可见,该星座时统技术方案具有很大程度上的自主性。

星上时间管理单元自主时统处理的关键,在于时间管理单元具备准确跟踪真实的星地时差Δαk变化趋势的能力,星上采用如下二次模型来跟踪真实星地时差的时变趋势[5]。

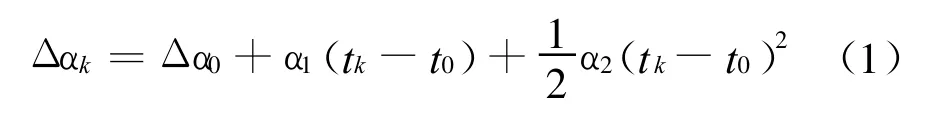
其中,Δα0表示起始预报时刻t0的星地时差量;α1和α2分别表示星上时钟相对地面系统时钟的频差和频漂率估计值。然而,依据上述模型对星地时差进行跟踪,其跟踪误差将随预报时间间隔tk-t0的增加而快速增加(tk为k个预报时刻)。为了保证长期准确跟踪时差,需要利用不时获得的星地时差观测量,通过在线估计器,对模型变量进行在线估计,并周期性地替换原有的模型变量估计(需要改变起始预报时刻t0)。

2.2 星地时差观测

地面站和星座各星上的GNSS 接收机(其内部时钟被屏蔽,实际采用地面站或星上时钟信号)各自测得地面系统时钟、各星上时钟相对于GNSS系统时钟的相位差。其原理为GNSS 定位原理[5]

在得到Δαjsys观测量之后,记地面系统时钟相对GNSS系统时钟的时差为Δα0sys,星座星的时钟相对GNSS系统时钟的时差为Δαjsys(j =1,2,…,n),则每颗星座星时钟相对地面系统时钟的时差观测量为

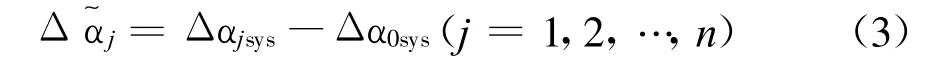
2.3 时差预报模型变量估计

时差模型变量估计是一个状态估计问题,其状态量为

离散的状态方程和观测方程为

其中

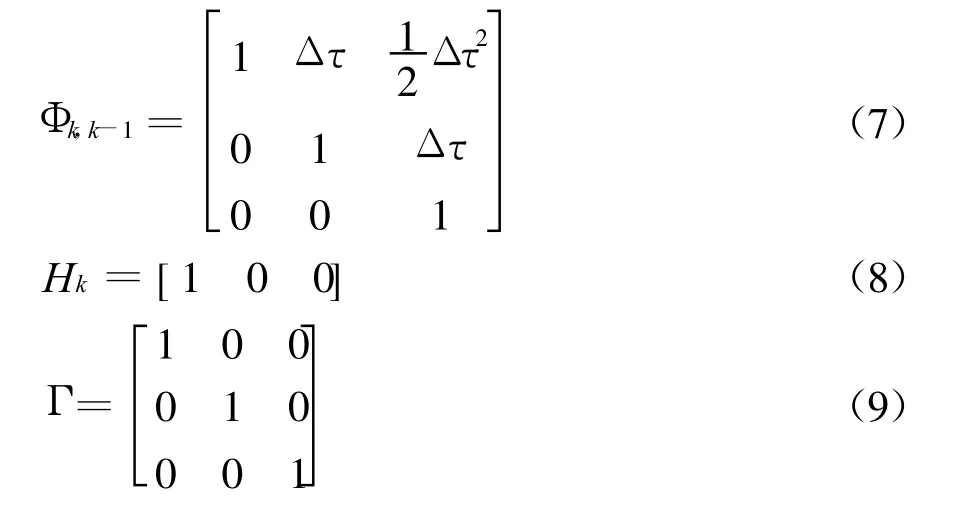
Δτ表示离散周期;wk表示时钟的随机过程噪声;vk表示随机时差观测噪声;xk表示k时刻的状态量;zk表示k时刻的观测量。

上述状态估计问题通常可用文献[6]给出的KF 来解决。

2.4 自主调相处理

当星地秒脉冲相位差满足如下条件时

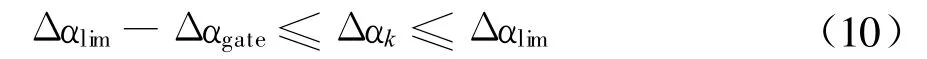
星上时间管理单元判断调相时机已到。其中,Δαlim和Δαgate分别称为调相指标和调相阈值(其值大小反映调相的敏感度)。由于当前真实时差量未知,所以需要利用时差预报量(或估计量)。

采用名义调相残差最小策略,需要调整的相位差为

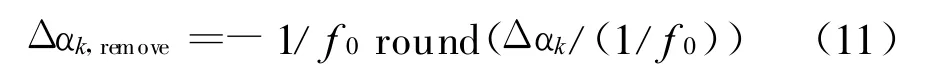
其中,f0为时钟基频;round(·)表示按照四舍五入原则取整操作;相应的名义调相残差为

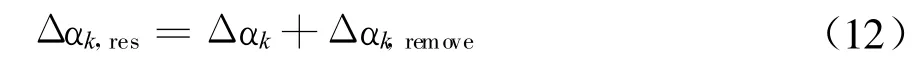
3 半实物仿真方案设计

3.1 任务场景设想

一个近地通信卫星星座,是典型的Walker(24/3/1)星座,卫星轨道高度1 000km,并考虑一个地面站,以10°最低观测仰角计算,该系统可以保障任何时候都至少有1颗卫星在地面站的服务范围内,同轨面内的相邻星间时刻存在稳定持续的链路,而任意两个异轨道面之间也有适宜的星间链路,因此,该星座系统可以保证星座任意卫星与地面站之间处于时时刻刻的连通状态。为了实现星座系统任务,要求星座各卫星与地面站的秒脉冲相位差保持在一定范围内。假设两者同步精度要求为100ns。

3.2 半实物仿真方案设想

考虑到该时统方案下星间链路不参与星间时差观测,而只是将地面GPS时差观测数据传输到近地星座各卫星,可以说,各近地卫星的星地时统是相对独立的,因此,对一颗近地卫星的星地时统进行考察,可以在很大程度上反映出整个近地星座系统的星地时统能力。考虑到所需硬件成本和数量的要求很高,本文仅提出一个半实物仿真原理方案,如图1所示。

上述仿真平台架构方案共包括三部分内容。

1)星上(单星)相关时统部分:1台GPS 接收机和1台时间管理单元(外接1台时钟)。为了弥补现有时间管理单元数据处理能力的不足,利用1台工控机完成时间管理单元中的时差数据在线处理工作。

2)地上(单地面站)相关时统部分:1台GPS 接收机和1台时间管理单元(外接1台时钟)。同样,利用1台工控机完成时间管理单元中的时差数据在线处理工作。

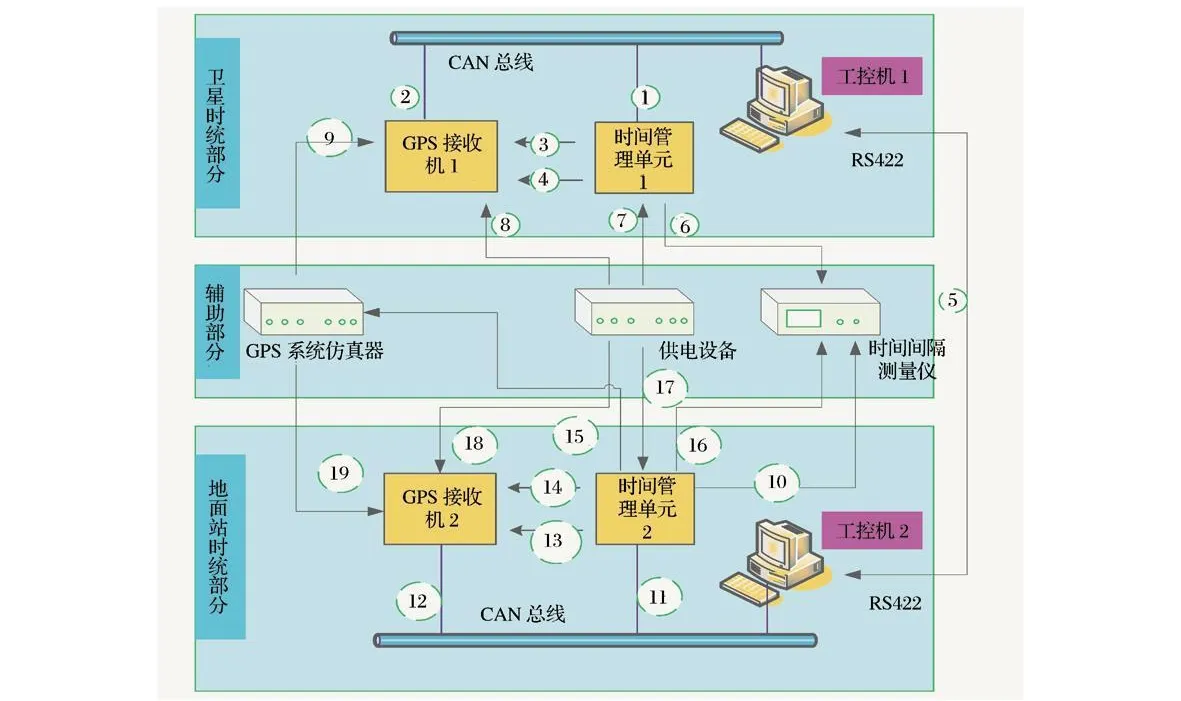
图1 时间同步半实物仿真原理图Fig.1 Plan of GPS-based time synchronization hardware-in-the-loop simulation

3)辅助部分:1台GPS系统仿真器和1 套仿真平台供电设备以及1台真实时差观测设备。此外,地面工控机还承担仿真管控的作用,也是辅助仿真的设备之一。

考虑到现有条件,星上和地上所用的GPS 接收机、时间管理单元和工控机都采用了同类型产品,不同之处在于星上时间管理单元采用外接铷钟,而地上则外接了更高性能的铯钟。有关设备的配置情况见表1。

根据原理图1,将表1所示设备连接起来的半实物仿真平台如图2所示。

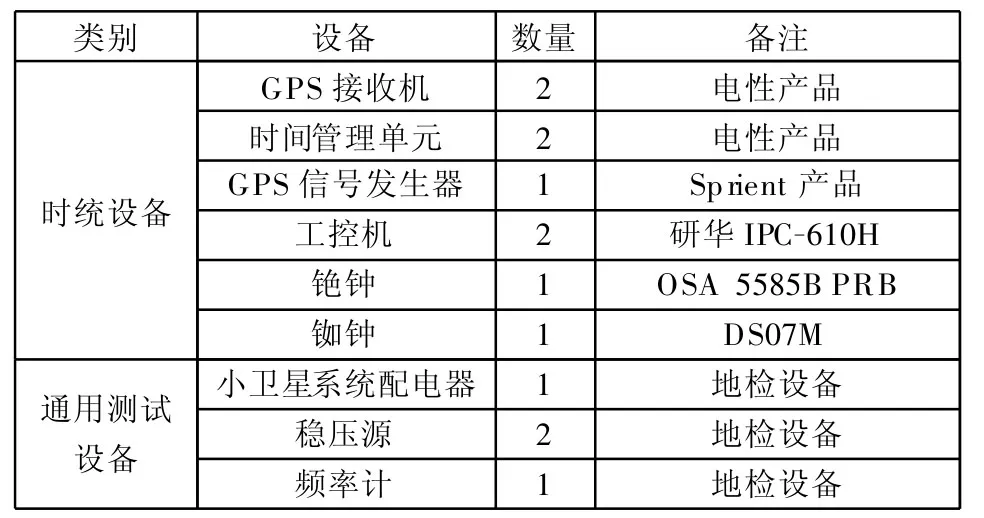
表1 仿真设备Table1 Chosen equipments for the hardwarein-the-loop simulation

图2 时间同步半实物仿真设备连接图Fig.2 Hardware-in-the-loop simulation of GPS-based time synchronization

4 半物理仿真结果与分析

4.1 仿真设置

半物理仿真按照图3所示进行参数设置。其中,星地秒脉冲同步(调相)指标和调相阈值分别为

周期设置:系统仿真周期、时差观测周期、时差预报模型变量替换周期和时差预报周期皆设置为4s。

图3 仿真参数设置Fig.3 Parameters set ting of simulation

至于数学仿真,还需要仿真出地面站时钟相对GPS系统时钟的时差观测量,以及星上时钟相对GPS系统时钟的时差观测量。由于真实参数和模型未知,根据星地时钟产品的名义性能参数和GPS系统时钟的大致性能了解,并依据式(1)所示的简单模型仿真出这些时差观测量信息。随机观测噪声选择白噪声,均方差假设为50ns。

4.2 仿真结果与分析

数学仿真结果如图4～图6所示。其中,图4(上)给出了基于GPS系统的星地时差观测量,受到如图4(下)所示的100ns 量级的随机观测噪声的干扰影响。图5(上)给出了在线时差滤波器的星地秒脉冲相位偏差估计的误差,结果显然是一致性收敛的,图5(下)给出了星上时差预报模型的误差。不难看出,这两图趋势几乎一致,原因在于,时差预报模型变量替换周期等于观测更新周期,即,每个更新时刻的滤波估计值都用于替换预报模型的上一个参数估计。图6给出了不采用(上)/采用(下)自主调相措施下的星地秒脉冲相位差。不难看出,若无自主调相措施,星地秒脉冲不可能控制在指标要求的范围内。

半实物仿真给出的星地秒脉冲相位差估计和观测量结果如图7所示,可以看出:

1)同数学仿真一样,星地秒脉冲相位差的绝对值一直被控制在100ns 以内,这说明星上自主时统处理成功实现了对调相时机的判断、调相量的计算以及调相指令的发送,而时间管理单元的秒脉冲发生器也成功地进行了相应的调整。

2)星地秒脉冲相位差的观测量随机分布在线性增长的真实相位差附近有限区域内,分布区域大小显示随机观测误差高于100ns(尚不包括无数据输出的异常情况)。不难理解,单纯的星地时差观测无法准确跟踪星地秒脉冲相位差,也无法据此达到相位同步指标要求。上述结果反过来说明,滤波器很好地估计出真实相位差及其变化趋势,故而时间管理单元才能准确判断出自主调相时机,计算调相量并发出调相指令。

3)星上自主时统处理流程成功实现了单星的时统目标。由于这种时统方案下各星同步相对独立,只要星间链路能够发挥数据传输的功能,本文所提的时统方法可望实现整个星座系统的星地时统目 标。

图4 星地时差观测量(上)与随机观测误差(下)Fig.4 Observations(upper)and random errors(lower)

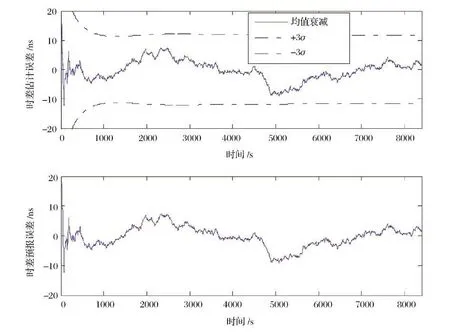
图5 时差估计(上)与时差预报误差(下)Fig.5 Estimation errors(upper)and prediction errors(lower)

需要指出的是:

1)半实物仿真中采用的G PS 仿真器的时钟性能相当于高稳晶振产品,远低于地面铯钟和星上铷钟的性能,这导致星地相位差的随机观测误差大大增大(将近200ns),而实际的GPS导航系统时钟相对仿真中所用的铯钟和铷钟来说更准确、更稳定,故而相位差的观测精度将有所提高。换句话说,半实物仿真的硬件配置条件相比真实情况来说更恶劣,但是,这个自主时统方案仍然达到了星地同步指标要求。

2)半物理仿真结果与数学仿真结果存在一些微小差别,主因在于数学仿真对星/地时钟、GPS系统时间等参数的设置与半实物仿真中的情况有差别,由于真实参数/模型不可精确得知,数学仿真采用名义上的参数和简单模型必然存在较大差别。但这两类仿真结果都很好地说明这套时统方案的可行性与有效性。

图6 未校准的星地秒脉冲偏差(上)与时统后的偏差(下)Fig.6 Phase errors of PPS before(upper)/after(low er)calibration

图7 半实物仿真结果采样Fig.7 Phase errors of one satellite PPS relative to the ground PPS

5 结论

本文为近地卫星星座系统提出一个利用全球导航卫星系统(GNSS)实现全网星地秒脉冲相位同步的时统方法,并提出一个半实物仿真方案对此加以验证。数学仿真与半实物仿真的结果都表明,近地卫星星座系统基于GPS 类GNSS系统可以实现高精度的星地时间同步,证实了星上时间管理单元自主时统处理流程的正确性。

随着我国自主研发的GNSS系统的建立,本文所提出的星座系统时统方法可以避免系统安全性方面的隐患,也有望大大降低此类星座系统的维护成本。

References)

[1]郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].中国人民解放军信息工程大学,2006

[2]帅平.导航星座的自主导航技术——卫星自主时间同步[J].飞行器测控学报,2004:23(4)11-15

[3]惠卫华,卢晓春,华宇,等.卫星星座时间同步方法的研究和仿真[C]//西安:2005年全国时间频率学术交流会议,2005:47-51

[4]聂桂根.高精度GPS 测时与时间传递的误差分析及应用研究[D].武汉大学,2002

[5]童宝润.时间统一系统[M].北京:国防工业出版社,2003

[6]Stein S R,Evans J.The application of Kalman filters and ARIM Amodels to the study of time prediction errors of clocks for use in the defense communication system[C]//44thAnnual Symposium on Frequency Control.1990:630-635