一种航天器加筋锥壳结构轴压稳定性研究

2010-12-26陈同祥阮剑华柴洪友

航天器工程 2010年6期

康健陈同祥阮剑华柴洪友

(1 中国空间技术研究院,北京100094)

(2 北京空间飞行器总体设计部,北京100094)

1 引言

航天器结构设计的最基本要求就是结构不发生破坏或失稳[1]。加筋锥壳结构是一种半硬壳式结构,在承受轴向和横向载荷时,存在3 种失稳形式[2-8]:1)蒙皮失稳:即在两个相邻桁条与隔框之间的小块蒙皮失稳,该失稳形式实质上是圆柱曲板的失稳,屈曲应力较低;2)壳段失稳:指相邻的隔框之间由蒙皮桁条组成的结构失稳;3)整体失稳:当框的刚度不足时,则屈曲将扩大到几个隔框的范围,即发生结构的整体失稳。航天器结构设计中,蒙皮弹性的局部失稳是允许的,但整体失稳往往是毁灭性的,任何设计都应该避免结构的整体失稳[9]。

本文着重研究使用有限元方法分析加筋锥壳结构轴压稳定性问题时,开口型截面桁条的模拟形式对稳定性分析结果的影响;并用平板/加筋圆筒极限轴压的有效宽度法计算其整体失稳时的极限载荷。与某航天器加筋锥壳结构的静力试验结果对比,得出了加筋锥壳结构稳定性分析方法。

2 稳定性计算原理及有限元分析方法

欧拉失稳的概念从一端固定一端自由的轴压理想柱出发,给出压杆的临界载荷。稳定性分析的有限元基本方程为

式(1)中K为结构的整体刚度矩阵;KG为结构的几何刚度矩阵;λ为结构稳定性系数;u为位移。

如果求出λ,则结构的失稳临界载荷为

式(2)中Fb为基态载荷,是扰动载荷ΔF 作用前施加于结构的载荷,包括初始内压、温度载荷、非零初位移等,代表了在扰动载荷作用前结构的初始状态。

如果结构上没有基态载荷作用时,则失稳临界载荷可以直接表达为

式(3)中F为外载荷。

在数学上,求解方程(1)为典型的广义特征值问题,即求解特征值和相应的特征向量,特征值和特征向量分别表征临界载荷的大小及相应的失稳形式。

对于金属圆筒(锥)薄壳,一般做法是将金属桁条、隔框用点焊或铆接的方法固结在一起。开口型截面(如π型)成型简单,可操作性强,可以提供良好的与蒙皮点焊或铆接界面。π型截面金属桁条点焊或铆接到金属锥壳蒙皮上后,桁条外形截面与焊点或铆钉间的蒙皮组成了封闭空间,承受轴压和剪切载荷作用时桁条稳定性显著增强[10]。

使用有限元分析软件M SC.NAST RAN 对开口截面(π型)加筋锥壳结构进行稳定性分析。金属蒙皮一般用板壳单元模拟,金属桁条可以用壳体单元或梁单元模拟,桁条模拟形式的不同对稳定性计算结果有很大影响。图1为用壳体单元模拟桁条的形式(简化形式1),图2为用π型截面梁模拟桁条的形式(简化形式2),图3为用与π型桁条等截面积的框形截面梁模拟桁条的形式(简化形式3),简化形式2 和简化形式3 均未考虑桁条偏置,即模拟桁条的梁单元截面形心位于蒙皮上,图4的简化形式4 在简化形式3 的基础上考虑了桁条偏置。以上4 种简化形式中,简化形式2 和简化形式3 最容易建模,简化形式1 和简化形式4 的模型比较复杂。

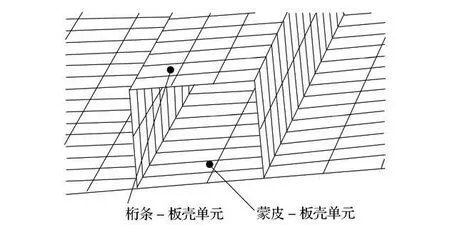
图1 桁条简化形式1Fig.1 Form 1 of the stringer

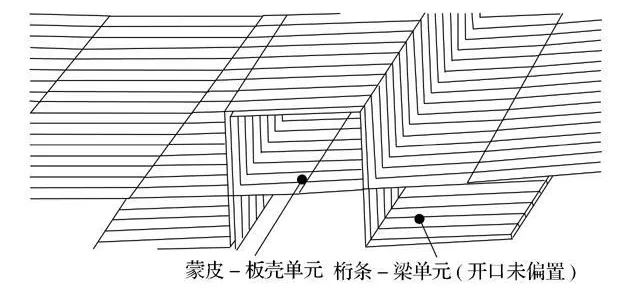
图2 桁条简化形式2Fig.2 Form 2 of the stringer

图3 桁条简化形式3Fig.3 Form 3 of the stringer

图4 桁条简化形式4Fig.4 Form 4 of the stringer

假设加筋锥壳结构半径较小的一端固定在水平界面,半径较大的端面作为刚性界面承受轴压力,对以上4 种简化形式分别进行稳定性分析,输出应力和稳定性计算结果,见表1。

表1 应力及稳定性计算结果Table1 Results of stress and stability

由表1可知,4 种简化形式应力计算结果受到加筋模拟形式的影响很小;稳定系数受到桁条模拟形式影响较大,简化形式2 计算的稳定性系数最低,简化形式3 计算的稳定性系数约为简化形式2 的2倍,简化形式1 计算的稳定性系数最高,约为简化形式2 的3倍,考虑梁单元偏置的简化形式4 稳定性系数比简化形式3 略低。

简化形式2 的稳定性计算结果是不合理的,因为实际结构中桁条与焊点或铆钉间的蒙皮构成了封闭截面,而不是简化形式2 有限元模型中的开口截面,采用何种简化形式进行稳定性分析更接近于实际设计状态,需要用试验结果验证。

3 加筋圆筒极限载荷的计算方法

对于半硬壳式结构,采用有限元分析可以得到局部失稳临界载荷和对应的失稳波形,并在后处理软件中直观显示,但较难计算出结构的整体失稳的极限载荷。因此,本文用平板/加筋圆筒极限轴压的有效宽度法[4]计算整体失稳时的极限载荷。计算轴压极限载荷时,均将框作为桁条的节点。桁条间曲板的曲率参数为

式(4)中,b为桁条间曲板弧长,t为蒙皮厚度,R为圆筒/锥半径。υ为泊松比,若曲率参数z ≤40,曲板皱损后性能接近平板,由于桁条是主承力构件,可采用平板的有效宽度法计算极限载荷;若曲率参数大于40,则应采用加筋圆筒的有效宽度法。

3.1 平板的有效宽度法

用平板的有效宽度法计算极限载荷Tjx的公式为

式(5)～(7)中,E为材料的弹性模量,n为桁条数目,σht为桁条临界应力,f为桁条截面面积,φ为蒙皮宽度的减缩系数,ξ为蒙皮失稳引起桁条临界应力降低后的有效系数,其取值见表2。

表2 有效系数取值Table2 Value of coefficient

3.2 加筋圆筒的有效宽度法

当曲率参数较大时,按照平板有效宽度法计算极限载荷一般低于加筋圆筒轴压极限承载能力,因此发展了加筋圆筒的有效宽度法,根据加筋圆筒的主承力构件是桁条,曲板临界应力σmp为圆筒临界应力σyt与平板临σmp界应力σpb之和,即

假定曲板失稳后,圆筒部分下临界应力保持不变,对平板部分的轴力随桁条应力升高而增加,直至桁条失稳,结构失去承载能力,即极限载荷Tjx为:

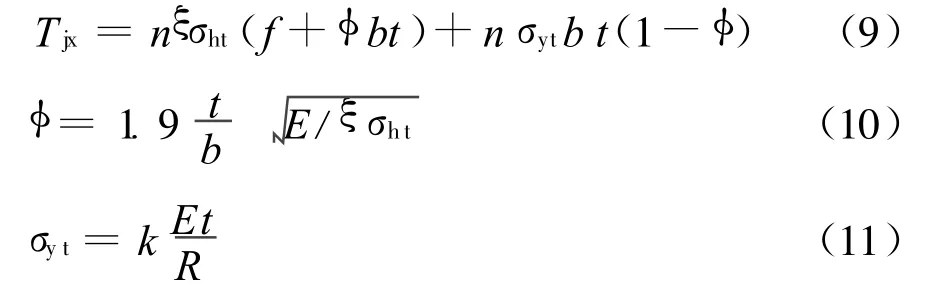
4 加筋锥壳结构稳定性分析与验证

某航天器采用了加筋锥壳结构,使用有限元分析软件MSC/NAS TRAN 对其进行稳定性分析以确定其稳定系数,该航天器加筋锥壳没有安装精度要求,允许发生局部弹性蒙皮失稳。采用极限载荷的计算方法对其极限承载能力进行估算,其桁条间曲板的曲率参数为36,若采用平板的极限载荷法,则极限载荷约为1 140kN,若采用加筋圆筒的极限载荷法,其极限载荷约为1 360kN。

对该加筋锥壳结构进行静力试验,对稳定性分析结果进行验证。锥壳半径较小的一端固定在水平界面,半径较大的端面与刚性的加载工装连接,工装加载点位于圆锥轴线上,施加沿轴向的轴压载荷,试验过程中进行应变和位移监测。通过试验中蒙皮应变测点的载荷-应变曲线可以确定蒙皮局部失稳时的临界载荷及稳定性系数,卸载后应变测点无较大残余应变,说明该蒙皮为弹性失稳。进行超载试验以验证其极限承载能力,施加最大轴向当量载荷约为1 260kN,加筋锥壳大部分蒙皮失稳,隔框间桁条发生屈服,卸载后有较大残余变形,认为1 260kN已接近其极限载荷。