一类带液体晃动航天器的姿态控制

2010-12-11张洪华

空间控制技术与应用 2010年2期

关键词：姿态控制滑模航天器

杜辉，张洪华

(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术国家级重点实验室, 北京 100190)

一类带液体晃动航天器的姿态控制

杜辉1,2，张洪华1,2

(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术国家级重点实验室, 北京 100190)

针对一类带液体晃动的航天器，在建立系统数学模型的基础上，利用一种分层滑模的设计方法来设计控制器.将系统状态变量分成可自行到达平衡位置和需要施加控制才能到达平衡位置两部分，对于需要施加控制达到预定平衡位置的状态变量，用分层滑模控制来设计控制律，将其分解成两个子系统，分别构造滑动平面，采用Lyapunov方法求取总控制量.当系统接近平衡位置时，双层滑模控制器退化成单层控制器，保证系统能够稳定在最终的平衡位置上.仿真结果表明，该方法能很好地达到控制效果.

液体晃动; 分层滑模控制; 变结构控制航天器

当前，航天事业的发展要求不断提高航天器的运载能力，延长航天器工作寿命及提高其运动的稳定性.因此液体燃料占航天器总重量的比值相应加大.当贮箱部分充满液体燃料时，在平动和转动中，液体燃料不断晃动，对航天器产生显著的干扰力、干扰力矩和冲击压力，使航天器呈现非线性、参数时变等复杂的动力学行为，对航天器的姿态控制和稳定性产生重大影响.1969年ATS-V航天器和2000年NEAR航天器的失效以及2007年Space X运载火箭发射失败均是由贮箱内液体燃料晃动所导致的[1].因此如何抑制液体燃料晃动对航天器姿态控制的干扰是一个难点.目前，抑制晃动干扰的控制方法有：文献[1]针对带液体晃动航天器设计了自适应极点配置姿态控制器；文献[2]用退步法设计了带液体晃动的航天器姿态控制器；文献[3]针对带液体晃动的火箭设计了姿态控制器和晃动观测器；文献[4]针对带液体晃动的移动容器设计了滑模控制器；以及针对工业上液体的晃动所采用的其他控制方法[5-6]等.

针对加速度条件下带有液体晃动的航天器，本文利用分层滑模控制方法[7]设计了姿态控制器，在将航天器控制到目标状态的同时抑制液体燃料的晃动，仿真实例验证了该方法的有效性.

1 带液体晃动的航天器的数学模型

带液体晃动的航天器的姿态控制对航天器变轨、交会对接以及姿态跟踪目标的达成非常重要.本文研究的是有加速度条件下，在某固定平面内运动的带液体晃动的刚体航天器动力学与姿态控制.如图1所示.

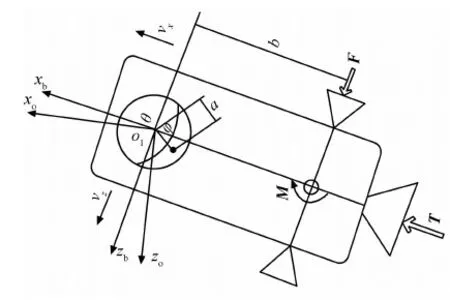
图1 带液体晃动的航天器示意图

如图1所示，建立航天器轨道坐标系o1xoyozo和本体坐标系o1xbybzb.带液体晃动的航天器可抽象成以下模型：航天器质量为m，转动惯量为I；晃动液体的质量为mf，转动惯量为If，晃动等效单摆的摆长为a；推力T为沿本体坐标系xb轴的常值推力，液体不晃时，T的方向过航天器质心；控制力F和控制力矩M为姿态控制输入；vx、vz分别为航天器沿xb轴和zb轴的速度；θ为航天器绕yo轴转过的角度；φ为液体晃动等效单摆相对航天器zb轴偏转的角度；ε为晃动的能量耗散系数.用T、F和M分别表示矢量T、F和M的大小.

由文献[2]可知带液体晃动的航天器动力学方程为

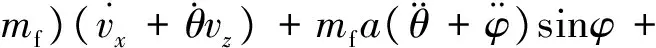
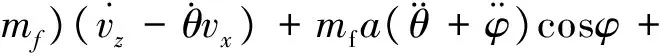
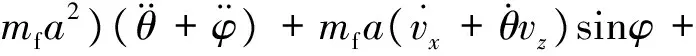
建立模型的前提条件：推力T较大，且为恒定常值，不考虑液体燃料的消耗.

基于上述模型条件，方程(1)可以改写为

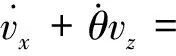
在航天器机动时，若姿态角变化较小，晃动为微幅晃动时，虽然液体晃动对沿xb轴方向的加速度有影响，但影响较小，因此可以用下面近似的等式代替：

令

其中，

2 分层滑模控制器设计

考虑如下形式的非线性系统：

其中：X=[x1,x2,x3,x4]T是状态变量；f1(X)、f2(X)是非线性函数；b1(X)、b2(X)为已知的控制项非线性函数；u为系统的控制输入.(x1,x2)和(x3,x4)分别作为两个子系统的状态变量，它们之间是耦合的，控制的目的是通过一个控制输入u使得两组系统状态分别达到各自的期望指标.

系统(8)的滑模控制器设计如下：首先根据其组成将系统分成几个子系统，对各个子系统分别定义第1层滑动平面，然后用第1层滑动平面构造第2层滑动平面，由此形成具有双层结构的分层滑模控制器.分层滑模控制器如图2所示.

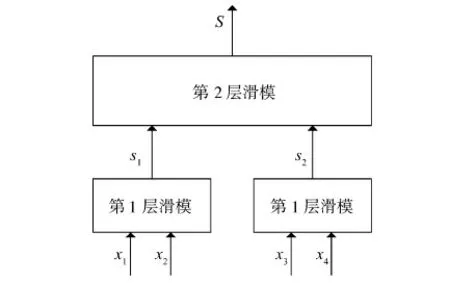
图2 分层滑模控制器的结构示意图

利用(x1,x2)和(x3,x4)这两组子系统状态变量，分别构造系统的滑动平面s1,s2，将其作为整个分层滑模控制器的第1层，形式如下：

其中，c1gt;0,c2gt;0.

采用等效控制法分别求得各个子系统在滑动平面上的等效控制量ueq1,ueq2.

由

可得

同理可求得

对于系统(8)而言，为了使各个子系统能够沿各自的滑动平面运动，必须在总的控制量中包含各个子系统的等效控制分量.因此，取总的控制量为

其中，usw为系统在趋近段的切换控制分量.

下面利用Lyapunov稳定性原理来构造切换控制量usw.

构造第2层滑动平面S

式中α为常数.

取Lyapunov能量函数为

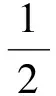
对上式进行求导(将b1(X),b2(X)简写为b1,b2)，可得：

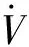
=S[α(c1x2+f1(X)+b1u)+

(c2x4+f2(X)+b2u)]

将u=ueq1+ueq2+usw代入上式，整理后可得

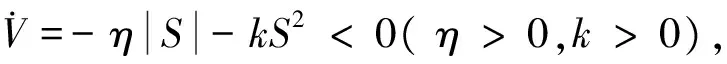
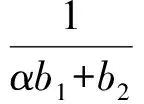
由Lyapunov稳定性原理可知：对于系统(8)，当总控制量为式(16)时，整个闭环系统是稳定的.

3 带液体晃动的航天器姿态控制器设计

本文利用文献[7]的方法，针对带液体晃动的航天器系统设计了分层滑模姿态控制器.

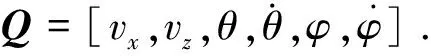
为了达到控制目标，令设计的控制约束为

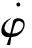
其中λgt;0表示液体晃动的期望衰减速率.这点对后面的控制器的设计至关重要.

系统相应化简为如下形式：

令

则子系统(20)可写成如下形式：

按上文中分层滑模控制器的设计方法来设计带液体晃动的航天器的姿态控制器.

构造第1层滑动平面：

其中：c1gt;0,c2gt;0.

利用等效控制法求得子系统(20)的等效控制量分别为

构造第2层滑动平面：

然后利用Lyapunov稳定定理求得切换控制量

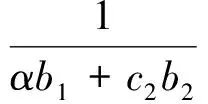
可求得总的控制量

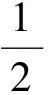
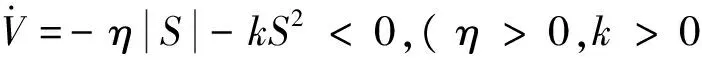
4 分层滑模控制器的稳定性分析

下面对所设计的各层滑动平面的稳定性进行分析，由文献[7]可得如下引理.

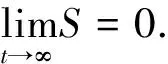
引理2[7].对于系统(22)，采用式(23)、(24)和 (27)所构造的双层滑动平面，采用式(29)所示的控制量，如果α的选择满足下列条件(30)，且当滑动平面s1,s2没有收敛到0时，sgn(s1·s2)为恒定值，则第1层子系统滑动平面s1,s2也是渐近稳定的.

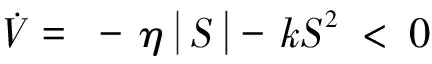
5 仿真实例

在仿真中，参数取值如下：

m=600kg,I=720kg·m-2,mf=100kg,

a=0.32m,b=0.25m,T=500N,

ε=0.19kg·m2·s-1，If=90kg·m-2.

初始值为

控制律参数为c1=5,c2=0.0005,α=40,η=0.0005,k=0.3,λ=0.48.

仿真曲线如图(3)～(7)所示.

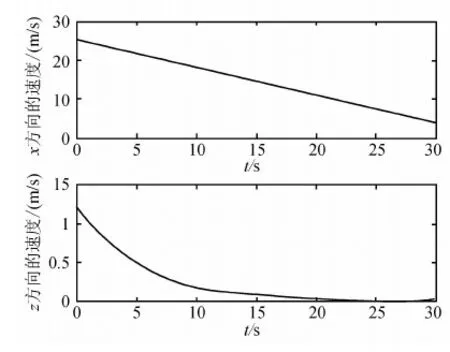
图3 vx,vz状态量的变化曲线

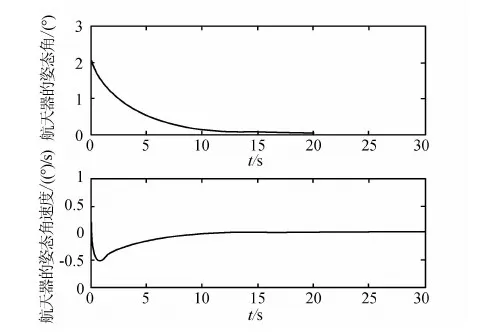
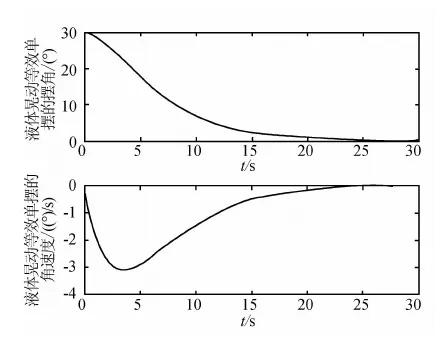
图状态量的变化曲线

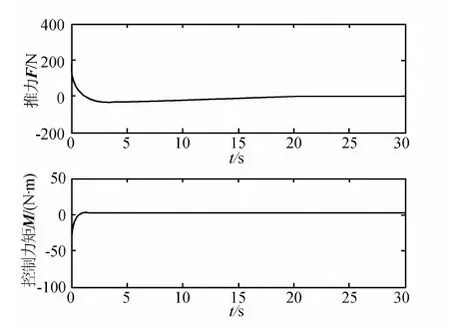
图6 F,M控制量的变化曲线

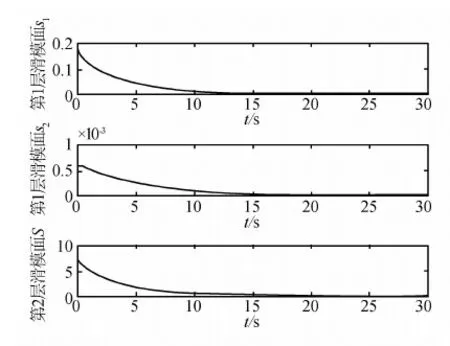
图7 各个滑模平面的变化曲线

从图(3)～(7)的仿真结果曲线可以看出，采用本文提出的控制器，系统能够很快到达平衡点，同时控制器输出很平滑，没有抖动.图(7)表明所有的滑模平面都是稳定的.所有的系统状态量都能在30s内稳定到平衡点.仿真结果表明了该方法的有效性.

6 结论

针对带液体晃动的航天器，本文建立了系统的数学模型.针对液体晃动与航天器姿态耦合及非线性等特点，设计了一种分层滑模分解控制器，按照这种方法设计的滑模控制器可以保证系统最终达到目标平衡点.文中给出的仿真实例说明了该方法的可行性与有效性.

[1] Shageer H, Tao G.Modeling and adaptive control of spacecraft with fuel slosh: overview and case studies[C].AIAA Guidance, Navigation, and Control, Hiton Head, South Carolina, August 20-23, 2007

[2] Reyhanoglu M, Cho S, McClamroch N H.Feedback control of a space vehicle with unactuated fuel slosh dynamics[C].AIAA Guidance, Navigation, and Control Conference and Exhibit, Denver, CO, August 14-17, 2000

[3] Krishnaswamy K, Bugajski D.Inversion based multibody control launch vehicle with fuel slosh[C].AIAA Guidance, Navigation and Control Conference and Exhibit, San Francisco, California, August 15-18，2005

[4] Kurode S, Bandyopadhyay B, Gandhi P S.Sliding mode control for slosh-free motion of a container using partial feedback linearization[C].IEEE 10thInternational Workshop on Variable Structure Systems, Antalya, Turkey, June 8-10, 2008

[5] Yano K, Terashima K.Robust liquid container transfer control for complete sloshing suppression [J].IEEE Transaction on Control Systems Technology, 2002, 10(4): 465-472

[6] Yano K, Terashima K.Sloshing suppression control of liquid transfer systems considering a 3-D transfer paths [J].IEEE/ASME Transactions On Mechanics, 2005, 10(1): 8-16

[7] 王伟，易建强，赵冬斌，等.Pendubot的一种分层滑模控制方法[J].控制理论与应用，2005，22(3)：417-422

AttitudeControlforaKindofSpacecraftwithFuelSlosh

DU Hui1,2, ZHANG Honghua1,2

(1.BeijingInstituteofControlEngineering,Beijing100190，China;2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190，China)

A hierarchical sliding-mode control design method is proposed for a kind of spacecraft with fuel slosh.The whole system is divided into two parts.The hierarchical sliding-mode control method is mainly used for the state variables which are not relative equilibrium ones.Using the Lyapunov method, a sliding-mode control law can be derived.When system states reach the equilibrium position, the hierarchical sliding-mode controller is degraded into the monolayer controller which guarantees the system to stabilize at the uppermost equilibrium position.Simulation results are given to illustrate the validity.

fuel slosh; hierarchical sliding-mode control; variable structure spacecraft