仅有相对视线角测量时的椭圆轨道交会相对导航分析*

2010-12-11解永春

空间控制技术与应用 2010年2期

关键词：交会视线机动

刘涛，解永春

(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术国家级重点实验室,北京 100190)

仅有相对视线角测量时的椭圆轨道交会相对导航分析*

刘涛1,2，解永春1,2

(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术国家级重点实验室,北京 100190)

对仅有相对视线角测量时的椭圆轨道交会相对导航问题进行了分析.借鉴已有研究成果，给出仅有相对视线角测量时，相对导航系统可观的定义，以及为使系统可观，加速度项所需满足的充分必要条件；分析指出由于相对动力学模型误差的存在，相对导航系统始终是可观的，但可观度很弱；而追踪器进行适当的机动可极大改善系统的可观性，给出为使系统可观，机动加速度具体所需满足的充分必要条件；指出当通过施加机动加速度改善系统的可观性时，获取零输入相对位置矢量方向是前提条件，并论证了利用相对视线角测量信息，可以对零输入相对位置矢量方向进行估计和预测.

椭圆轨道交会；相对视线角；相对导航；可观性

相对视线角是交会对接中比较容易获得的相对测量信息.在交会过程中，由于故障等原因可能造成敏感器部分功能失效；另外，微小卫星作为追踪器时，由于星上空间和能耗等限制因素，使得星上只能配备一些简单的相对测量敏感器.以上两种情况中都有可能导致追踪器仅仅能够获得相对视线角测量而无法直接获得相对距离测量.

目前，有关仅获得相对视线角测量时的相对导航问题的研究还比较少.文献[1]讨论了由宇航员利用六分仪等简单设备测量相对视线角进行交会的可行性，指出追踪器进行主动机动可以使相对导航系统可观；文献[2-3]通过数学仿真手段，利用线性协方差分析方法，对仅有相对视线角测量并辅助有追踪器机动情况下的相对导航问题进行了分析；文献[4-5]对该问题进行了比较深入的探讨，给出了为使系统可观，轨道机动加速度所需满足的充分必要条件.

文献[1-5]均针对近地近圆轨道交会问题，以Hill方程为基础进行了讨论，而对仅有相对视线角测量时的椭圆轨道交会相对导航问题，目前还没有明确的结论，本文将主要借鉴文献[4-5]的研究成果，对该问题进行研究.

1 相对导航系统描述

椭圆轨道交会中，两个航天器相距较近时，可以采用线性相对动力学模型，即T-H方程对相对运动进行近似描述.建立如下相对导航坐标系：原点为目标航天器的质心，z轴指向地球的质心，y轴垂直于z轴，指向轨道角速度方向，x轴与z、y轴构成右手系.在该坐标系中，T-H方程具体形式为

(1)

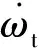
(2)

则式(1)所示的线性时变系统可写为如下状态方程形式：

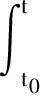
(3)

式中，

(4)

(5)

由追踪器指向目标器的相对视线由仰角α和方位角β描述，相应的测量方程为

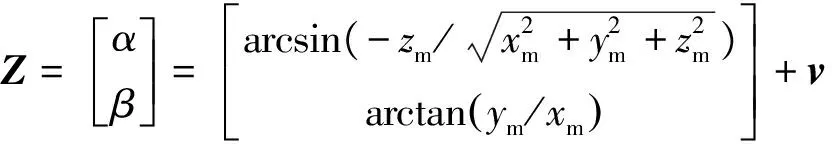
(6)

(7)

式中，v为测量噪声，Crm为相对导航坐标系到敏感器测量坐标系的方向余弦阵.

2 相对导航系统可观的定义

如式(3)所示的线性时变系统，系统状态方程完全由目标器轨道参数决定，而目标器轨道可以认为是实时已知的，故状态方程可以认为是实时已知的.另外，追踪器机动加速度也可以认为是已知的.可见，在初始时刻相对状态已知时，以后各时刻的相对状态均可直接求得.所以，相对导航系统的可观问题可以归结为初始时刻相对状态的确定问题.

借鉴文献[4]的思想，在仅可获得相对视线角测量时，给出椭圆轨道交会相对导航系统的可观性定义.

定义1.从任一初始时刻t0开始，在一定的观测时段内(t0lt;tlt;tf)，对于任意不同初始相对状态，所得到的相对视线角测量各不相同，则相对导航系统是可观的.要注意的是，定义中所指的视线角测量不考虑测量误差.

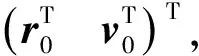
rt=Φrr(t,t0)r0+Φrv(t,t0)v0

(8)

相应的视线单位矢量为

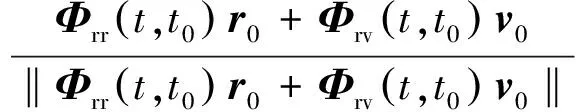
(9)

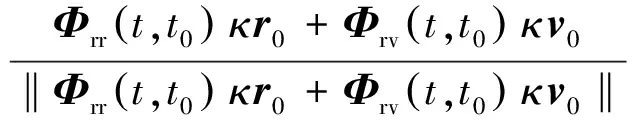
(10)

由定义1可知，该情况下相对导航系统是不可观的.

而若u≠0，t时刻的相对位置可表达为

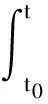
=rb,t+δrt

(11)

式中，rb,t是t时刻系统的零输入响应，这里称为零输入相对位置矢量，δrt是t时刻系统的相对位置增量.由定义1容易得到，使系统满足相对导航系统可观性定义的充分必要条件如下.

条件1.对于∀κgt;0,κ≠1，均∃t∈(t0,tf)使得式(12)成立：

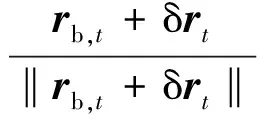
(12)

下面将分别就相对动力学模型误差等效加速度和追踪器轨道机动加速度对系统可观性的影响进行分析.

3 相对动力学模型误差对系统可观性的影响

椭圆轨道交会相对动力学模型本质上是非线性系统，T-H方程是对非线性系统线性化后得到的模型，因而存在建模误差，可将模型误差的影响等效看作是外力引起的加速度.本节将研究模型误差对相对导航系统可观性的影响，主要考虑二阶模型误差的影响，其他高阶项的影响与此类似.

若考虑引力加速度的二阶项，则相对动力学模型可写为

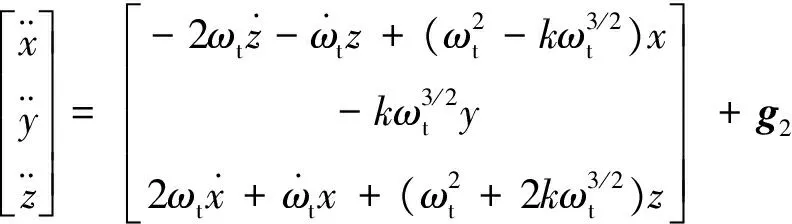
(13)

式中，

(14)

其中Rt为目标器地心距.加速度项g2的具体值由真实相对状态决定，为便于分析，可以用标称相对状态，即由T-H方程根据初始相对状态计算得到的相对状态，代替真实值进行分析.

由式(14)可知，当初始状态为

时，不同初始状态对应的模型误差等效加速度始终满足

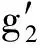
(15)

接下来分析如下结论：对任意标量函数a(t)，均∃t∈(t0,tf)，使得

≠a(t)[Φrr(t,t0)r0+Φrv(t,t0)v0]

(16)

要严格的通过解析方式验证式(16)成立，可以按照文献[6]的方法对相对动力学模型进行变量代换后进行分析，但由于系统是时变系统，该方法很繁琐，不便于问题的说明.本文借鉴文献[4]的做法，选择从定性的角度对该问题进行分析：式(13)右端第一项的特点是x轴方向和z轴方向的运动与y轴方向的运动是解耦的，而由g2的形式可以看到，x,z与y存在耦合项，因此式(16)是成立的，说明对于∀κgt;0,κ≠1一定∃t∈(t0,tf)，使得式(17)成立

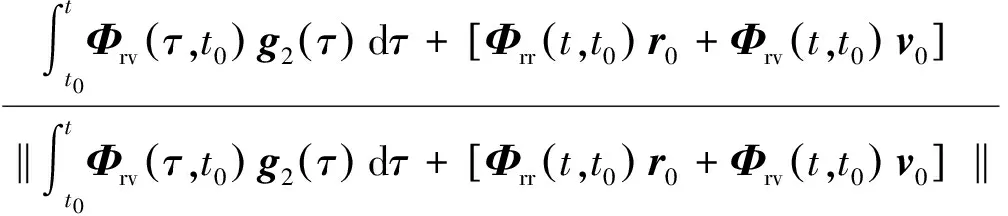
(17)

分析式(17)可知：任何初始状态所对应的相对视线角测量都不可能相同，进而由定义1可知相对导航系统是可观的.

通过以上分析可知，由于存在模型误差，所以相对导航系统始终是可观的.但是，相对距离比较近时，模型误差很小，对相对轨迹的影响也很弱，即不同初始条件下的相对轨迹可以很接近，利用带有测量误差的相对视线角测量可能根本无法区分出相对轨迹的不同，所以相对导航精度会很差.以上分析并不直观，下面本文利用基于奇异值分解的可观度分析方法[8]，对以上问题进行进一步深入分析.

考虑一般的线性时变离散系统

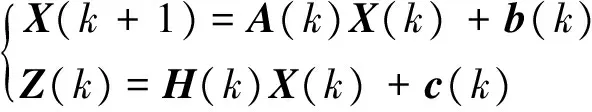
(18)

式中，X(k)为n维状态向量，Z(k)为m维输出向量，A(k)、b(k)、H(k)和c(k)是取决于时刻k的时变矩阵.

令

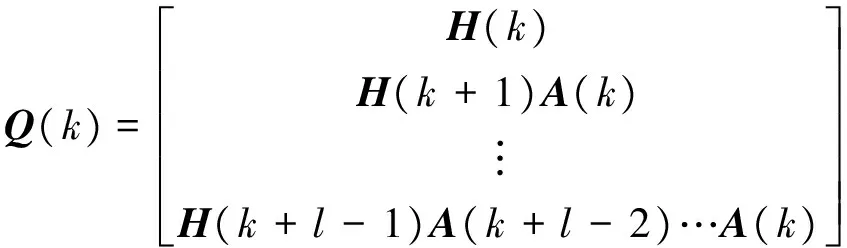
(19)

定义各个状态的可观度为

(20)

如式(20)所示，定义系统第i个状态的可观度，等于对系统可观性矩阵Q(k)进行奇异值分解后，利用奇异值倒数加权右奇异矩阵VT的第i列向量所得范数的倒数.本方法的特点是利用状态变化对相应输出变化的影响大小作为状态可观度的描述, 物理意义很明确.

以式(13)作为状态方程，式(5)作为测量方程，下面利用可观度分析方法就未建模动态对相对导航系统的影响进行数学仿真分析.需要指出的是：式(13)为非线性连续系统，需要进行线性化和离散化处理后才能进行系统的可观度分析.设定目标器轨道高度为400 km,偏心率为0.05，初始状态为

真实相对轨道通过目标器和追踪器轨道动力学模型进行求解，相应参数设定为l=6.

由图1可见，相对位置在所有时刻的可观度均大于零，从而说明由于建模误差的影响，系统的确是可观的.但是，除y轴外，x轴和z轴的可观度都很小.可观度小意味着状态间的差别比较小时，由此造成的系统输出间的偏差会更小，因此利用带有误差的测量很难区分出不同的状态，所以滤波估计精度会很差.

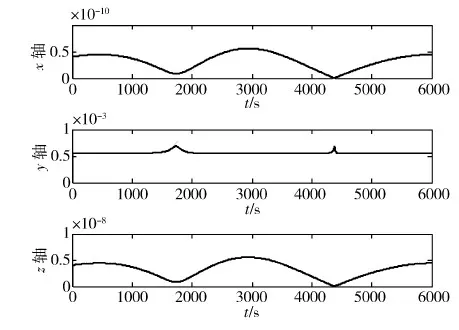
图1 相对位置的可观度

4 追踪器机动加速度对系统可观性的影响

相对动力学模型误差是系统固有的，由前面分析可知模型误差使得相对导航系统始终可观，但可观程度很弱.与相对动力学模型误差不同，追踪器轨道机动加速度通过人为施加，其大小和方向已知，故容易分析其对相对运动的影响.文献[1-5]中均指出，通过施加适当的轨道机动加速度可以改善相对导航系统的可观性.下面针对椭圆轨道交会问题，就轨道机动加速度对相对导航系统可观性的影响进行分析.

4.1轨道机动加速度所应满足的充分必要条件

式(12)已经给出了为使相对导航系统可观，加速度应满足的充分必要条件，但该条件应用起来并不方便.由于系统为线性时变系统，文献[4]中的结论仍适用，追踪器进行机动时，椭圆轨道交会相对导航系统可观的充分必要条件[4]可表述为：对于∀λgt;0,λ≠1，若系统满足条件2或条件3，则相对导航系统是可观的.

条件2.在观测时段(t0,tf)内，对于任意标量函数a(t)，均∃t∈(t0,tf)使得δrt≠a(t)rb,t；

条件3.在观测时段(t0,tf)内，虽然存在标量函数a(t)，使得任意时刻δrt=a(t)rb,t成立，但同时∃t∈(t0,tf)，使得a(t)lt;-1.

4.2系统可观的几何解释

图2中的rb为零输入相对位置矢量，δr为相对位置增量，r是真实相对位置矢量，θ为rb与r间的夹角.实际系统中，确定制导律后δr即为已知，r的方向可通过敏感器测量得到，所以若rb的方向已知，并且∃t∈(t0,tf)，使得0lt;θ(t)lt;180°,则由图2所示，矢量r和rb均可确定，即满足条件2时，系统是可观的；当θ=180°时，则意味着∃t∈(t0,tf)，使得追踪器穿过目标器，在该时刻可以确定出矢量rb，即满足条件3时，相对导航系统同样可观.

图2 系统可观的几何解释示意图

4.3零输入相对位置矢量方向的获取

由4.2节中的分析可知，实时获得零输入相对位置矢量rb的方向是通过追踪器机动改善系统可观性的前提，下面将从非线性系统可观性分析的角度，论证经过一定时段的观测后，系统能对rb的方向变化进行精确预测.

为便于分析，这里的相对视线定义为相对导航坐标系中由目标器指向追踪器的连线，这与第1节中所定义的测量坐标系中的相对视线不同，但这并不影响分析结论的正确性.相对导航坐标系中相对状态与球面坐标系中相对状态间的关系如下：

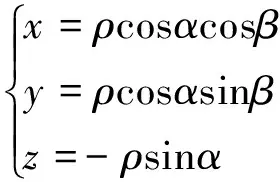
(21)

将式(21)代入式(1)，并设

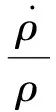
(22)

可以得到

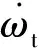
(23)

(24)

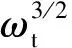
(25)

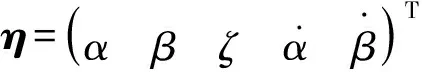
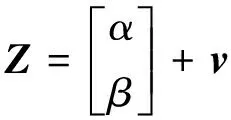
(26)

对于一般的非线性系统

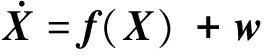
(27)

Z=h(X)+v

(28)

式中w为过程噪声，其可观性有以下结论.

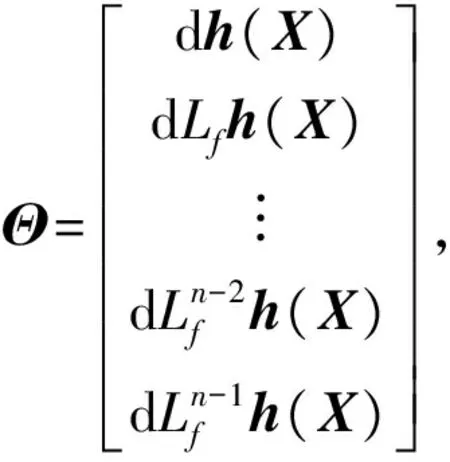
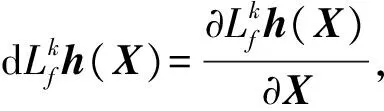
引理1[7].如果系统满足能观性秩条件，那么系统是局部弱可观的.

对于式(23)～(26)所描述的非线性系统可以得到以下结论.

定理1.空间椭圆轨道交会相对导航中，若仅仅利用视线仰角α和方位角β作为测量量时，由式(23)～(26)所描述的系统是局部弱可观的.

证明.对于式(23)～(26)描述的系统，易知

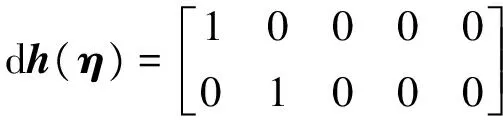
(29)

(30)

(31)

式(31)中的“*”表示矩阵中的元素，由于其具体形式不影响定理的证明，所以未给出.设

(32)

若rank(Θ1)lt;5，则意味以下两式同时成立

(33)

(34)

进而可推得

(35)

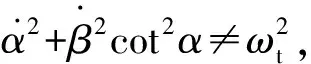
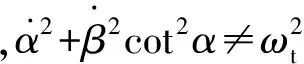
4.4影响相对导航系统可观性的两个重要因素

利用相对视线角测量进行相对导航设计的关键是如何利用相对视线角来确定相对距离.相对距离确定的精度直接影响到相对导航的精度，所以相对距离的确定精度可以作为系统可观性强弱的定性描述手段.下面分别分析相对视线角测量误差和零输入相对位置矢量方向确定误差对相对距离确定精度的影响.

(1)视线角测量误差[4]

若相对视线测量存在误差ε，由图3所示，容易得到

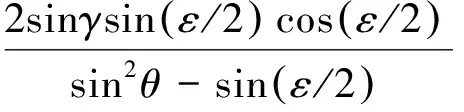
(36)

当ε≪1时，由式(36)可以得到

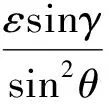
(37)

进行变型可以得到

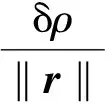
(38)

可见，相对距离的确定误差与测量误差成正比，而与sinθ大致成反比关系，所以为提高相对距离的确定精度，应该提高相对视线角测量精度以及采用适当的机动加速度，使θ接近90°.

(2) 零输入相对位置矢量方向确定误差

假设零输入相对位置矢量rb的方向确定存在Δθ的误差，由图4容易得到

(39)

当Δθ≪1时，由式(39)得

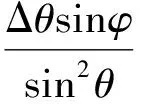
(40)

进而有

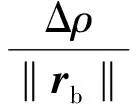
(41)

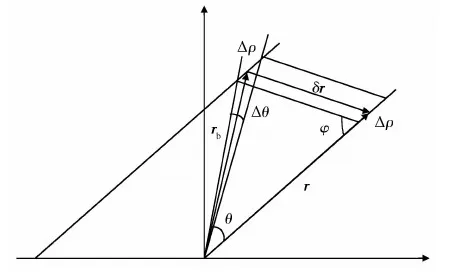
图4 零输入相对位置方向确定误差对相对距离确定的影响

可见，相对距离的确定误差与标称位置方向确定误差成正比，而与sinθ大致成反比关系，所以为提高相对距离的确定精度，应该提高零输入相对位置方向的确定精度.

5 数学仿真

本节将针对由式(1)和式(5)描述的系统，验证追踪器进行主动轨道机动能够改善相对导航系统可观性的结论.仿真所采用的真实数据与第3节中的相同.设定相对视线角测量噪声设定为零均值高斯白噪声，方差阵为

R=10-5×diag{2.4435,2.4435}

设定追踪器在第1次穿过x轴，即相对位置z=0时，通过脉冲进行主动机动，脉冲大小为Δv=-0.5vt，其中vt为变轨时刻的真实相对速度；滤波周期设定为1s，滤波器初始值设定为

其中，q为6维零均值高斯白噪声，模拟初始相对位置确定误差，其中相对位置误差的均方差设定为20 m，相对速度误差的均方差设定为0.2 m/s；过程噪声和测量噪声协方差阵取为

仿真结果如图5和图6所示.

图5和图6中的圆圈代表追踪器机动时刻.可以看到，在追踪器未进行主动机动时，相对状态的估计误差比较大，并且未能呈现收敛趋势，其中x轴和z轴相对状态的估计精度明显比y轴相对状态估计精度差，这与第5节中的可观度分析结果一致.追踪器进行主动机动后，估计误差明显减小，这证实了进行主动机动的确可改善相对导航系统的可观性.

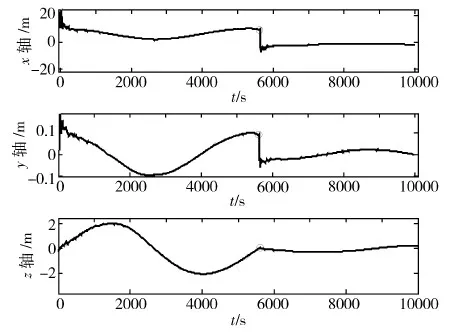
图5 相对位置估计误差

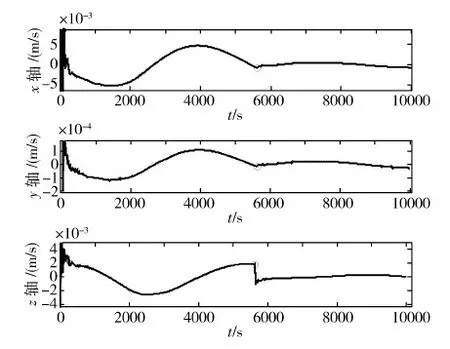
图6 相对速度估计误差

6 结束语

本文对仅有相对视线角测量时的椭圆轨道交会相对导航问题进行了比较全面的分析.借鉴已有的研究成果，给出了仅利用相对视线角测量时，相对导航系统可观的定义，分别就相对动力学模型误差和追踪器机动加速度对系统可观性的影响进行了分析，指出模型误差使得相对导航系统始终可观，但可观程度很弱，而适当的追踪器轨道机动加速度可改善系统的可观性，并对所得到的结论进行了仿真验证.仅仅利用相对视线角测量进行相对导航设计可以简化相对测量系统，节省能耗和星上空间，在未来的交会对接中有望得到应用，本文的研究成果为该方法在未来实际工程中得到应用提供了理论参考.如何兼顾轨道交会和相对导航要求，制定合理的制导策略是下一步需要进一步研究的问题.

[1] Schneider A M, Prussing J E, Timin M E A.Manual method for space rendezvous navigation and guidance[J].Journal of Spacecraft and Rockets, 1969, 6(9): 998-1006

[2] Chari R J V.Autonomous orbital rendezvous using angles-only navigation[D].Gambridge: Massachusetts Institute of Technology, 2001

[3] Chari R J V, Geller D K, Norris H L, et al.Autonomous orbital rendezvous using angles-only navigation[C].AAS/AIAA Astrodynamics Specialists Conference, Quebec City, Canada, July 30-August 2，2001

[4] Woffinden D.Angles-only navigation for autonomous orbital rendezvous[D].Logan: Utah State University, 2008

[5] Woffinden D, Geller D.Observability criteria for angles-only navigation[J].IEEE Transactions on Aamp;E Systems(to appear)

[6] Yamanaka K, Ankersen F.New state transition matrix for relative motion on an arbitrary elliptical orbit[J].Journal of Guidance, Control and Dynamics, 2002，25(1)：60-66

[7] 洪奕光, 程代展.非线性系统的分析与控制[M].北京: 科学出版社,2005:48-52

[8] 范伟,李勇.基于奇异值分解的航天器自主导航系统能观度分析[J].航天控制，2009，27(2):50-55

Angles-OnlyRelativeNavigationforEllipticalOrbitRendezvous

LIU Tao1,2, XIE Yongchun1,2

(1.BeijingInstituteofControlEngineering,Beijing100190，China; 2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190，China)

The problem of angles-only relative navigation for elliptical orbit rendezvous is analyzed in this paper.On the basis of other scholars’ achievements, the definition of the observability of relative navigation system with angles-only measurements is given, and the necessary and sufficient condition the input should satisfy to make the system observable is proposed, the paper points that the system is always observable because of the existence of dynamic model error, but the degree of observability is very week; in addition，appropriate maneuvering acceleration can improve the degree of observability, and the concrete necessary and sufficient condition the maneuvering acceleration should satisfy is deduced in the paper.At last, geometrical explanation of the system observability with maneuvering acceleration shows that it is essential to know the direction of the relative position vector without regard to maneuvering acceleration, and it can be proved that the direction of the relative position vector with zero input can be estimated and predicted using measurements for relative angles.

elliptical orbit rendezvous; angles-only relative navigation; observability