太阳帆板驱动装置建模及其驱动控制研究

2010-12-11斯祝华刘一武

空间控制技术与应用 2010年2期

关键词：帆板谐波力矩

斯祝华，刘一武，黎康

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190)

太阳帆板驱动装置建模及其驱动控制研究

斯祝华1,2，刘一武1,2，黎康1,2

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190)

综述了国内外太阳帆板驱动装置(SADA，solar array drive assembly)建模方面的相关研究情况，在此基础上建立了较为系统的SADA模型.模型综合考虑了电机驱动、电机模型、机构传动以及负载特性等因素，重点描述了摩擦和电机波动力矩，数学仿真和实验测试结果表明，模型具有一定的准确性和精确性.为提高帆板驱动性能，给出了两种可行的电流补偿方法，数学仿真结果表明两种补偿方法能大大改善帆板驱动平稳度.

SADA; 建模; 电流补偿

卫星在轨运行期间，为保证星上能源供应，太阳电池帆板需在SADA作用下相对星体转动跟踪太阳.由于步进电机定位精度高，无累计误差，长期运行时平均速率稳定度高，再加上驱动线路简单，易开环控制，因而在SADA中得到广泛应用.

国际上SADA的开发和应用起步早，很多国家都研制了自己的驱动机构，主要生产厂商有：美国MOOG，法国SEP、CNES，德法DORNIER，德国TELDIX，英国BAe，加拿大SPAR，印度ISRO，日本东芝和俄罗斯萨马拉专门设计局等.中国从20世纪80年代开展太阳帆板驱动机构的基础研究，目前国内研制单位有北京控制工程研究所和上海宇航系统工程研究所[1].

尽管国内外SADA研制厂商较多，但有关SADA驱动建模的研究文献较少，不过大量文献都指出了影响SADA驱动性能的两个重要因素——摩擦力矩和电机谐波力矩.CNES在设计SPOT卫星SADA时[2-3]曾指出，帆板转速波动是由滚珠轴承、导电滑环组件的摩擦力矩噪声以及电机的不完美引起的干扰力矩造成的.SPAR公司[4]通过实验测试表明SADA驱动速度的变化、电机摩擦都影响到电机的平稳性，甚至是帆板的不连续运动.ISRO则花了大量精力研究高性能低谐波力矩步进电机[5]，以改善驱动平稳性.

现已公开发表的SADA模型多是从某一方面来描述帆板驱动.DORNIER公司[6]曾采用SADA简化模型来分析驱动特性，该模型没有考虑电机工作方式及动态过程，认为电机驱动力矩只有基频分量，对摩擦力矩描述也极为简化.MOOG公司[7]则完全从机构运动角度建立了SADA模型，用4个微分方程来描述卫星本体俯仰角、电机转子转角、谐波齿轮输出轴转角和帆板转角间的动力学方程.巴西空间研究院[8]所建模型考虑了较为复杂的步进电机方程，用3个自由度描述SADA机构运动，但是模型没有介绍电机控制，对摩擦描述也不够深入，而且太阳帆板为刚性结构.文献[9]引述的中国某卫星帆板驱动模型则是在DORNIER模型基础上，稍加了对摩擦的详细描述.文献[10]则是用神经网络优化方法，跳过物理建模过程，通过反复训练测试网络以达到建模目的.北京控制工程研究所对SADA数学建模缺乏深入研究，当前采用的SADA模型只考虑电机基频输出力矩、4次谐波定位力矩以及库仑摩擦力矩，没有考虑与负载的耦合作用.

由于步进电机模型复杂，SADA处于低速运转状态，加上步进电机受脉冲控制，动态响应差，通常在帆板驱动的同时，帆板转速存在明显的波动，直接影响着卫星姿态.另外，卫星帆板多为挠性结构，帆板驱动波动的同时，其挠性振动也会受激励，从而也给星体姿态造成影响[9].当前高分辨率成像卫星的研制已提上了日程，这类卫星一般要求优于1×10-4(°)/s的稳定度，因此有必要从模型角度研究卫星姿态稳定度的重要干扰因素之一——SADA.

本文综合分析了现有模型的不足，从机电系统角度建立了相对全面的SADA模型.该模型对影响SADA驱动平稳性的两个重要因素做了详细描述，考虑了电机工作方式和电机控制.数学仿真和实验测试结果表明了模型的准确性和精确性.最后，针对现有SADA开环驱动不足，在电流补偿方面做了初步探索，数学仿真结果表明帆板驱动平稳性得到较大的改善.

1 SADA建模

SADA可分为直接驱动型和间接驱动型，这里只针对直接驱动型，但建模思想可推广应用于间接驱动型.直接驱动型SADA包括驱动电机、导电环、角位置传感器、机构结构本体以及驱动线路等.驱动电机为300齿两相混合式步进电机，按双四拍方式运转，功率放大器为PWM，采用正余弦电流细分电路驱动.采取转角转速开环、电流闭环控制方式驱动，指令脉冲数控制帆板转角，脉冲频率控制帆板转速.

本文建模旨在重点描述SADA驱动的几个重要环节，包括步进电机、摩擦力矩、波动力矩和机构动力学.

1.1步进电机模型

步进电机发展至今已有近一个世纪，也涌现了各种模型，不考虑电机绕组磁滞、磁饱和等现象，两相混合式步进电机模型包括电压平衡方程、电机力矩方程和机械运动方程[11]，描述如下：

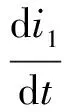
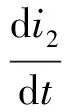
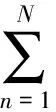
Te=T1+T2+Tcog

式中：θ、ω分别为电机输出轴转角和转速(即帆板转角和转速)；L为绕组自感；M为绕组间互感；Zr为电机转子齿数；R为绕组电阻；ii、ui为i相绕组电流、电压(i=1, 2)；n为谐波阶次；Te、Tf、TL和Td分别为电机电磁力矩、摩擦力矩、负载力矩和干扰力矩；Jm为电机转轴转动惯量；i3为假定的转子励磁电流，它为一常值；Lan、Lbn为相应阶次项系数.

从力矩方程可知，T1、T2为1、2相电流同转子永磁体产生的各次电磁力矩；Tcog为转子永磁体本身齿槽效应产生的齿槽力矩，同电流无关.

ui、ii由电机电流环PI控制决定，进而结合脉冲分配器，由PWM调制电机驱动电压.通常PWM开关频率较高，PWM环节可等效为增益为1的比例环节，则有电流控制闭环方程

1.2摩擦力矩

一般地，摩擦转矩与接触面间相对转速ω的关系可用非线性函数f(ω)描述，该函数同摩擦副的材料、表面状态和质量、润滑条件、温度等因素有关.目前工程上常用的经典静态摩擦模型有：①库仑摩擦+粘性摩擦模型；②Stribeck摩擦模型.考虑到SADA处于低速驱动状态，本文摩擦采用静态Stribeck模型描述[13].即

式中：ω为转速；ωs为临界Stribeck速度；Tc为库仑摩擦力矩；Ts为最大静摩擦力矩；σ0为粘性摩擦阻尼系数；sgn(·)为符号函数.

1.3波动力矩

电机波动力矩主要由转子齿槽效应和电机制造工艺引起，另外还同驱动器有关，包括齿槽力矩和电磁波动力矩两种[14].

齿槽效应是指电机转子旋转时，在定子齿槽作用下，电机气隙磁导会发生变化，从而导致磁阻力矩，齿槽力矩同绕组电流无关，只与转角有关，显然方程(2)中的Tcog就是齿槽定位力矩，对两相混合式步进电机而言，齿槽力矩只有相电流频率4n倍的谐波成分.

制造工艺引起的波动力矩主要包括：转子永磁体磁路分布不对称、不均匀引起的电磁谐波力矩；电机不对称引起的电流谐波，而导致的电磁谐波力矩.前者组成了方程(2)中的T1、T2，后者在模型中没有体现.

步进电机通常采用PWM控制，而且双四拍方式运行存在电流换向，这些都会导致电机绕组电流不是标准的正余弦电流，转矩波动不可避免.显然当考虑电机驱动工作方式时，模型就间接考虑了由此项因素引起的转矩波动，但通常电机电气时间常数较小，电流控制较好，这个转矩波动较小.

综上可知，方程(2)基本涵盖了步进电机的主要谐波力矩，未建模项只有电流谐波(电机制造工艺导致)引起的电磁谐波力矩，该项理论建模存在困难，需要具体到实际电机个体，同时考虑到现有电机制造工艺技术的提高，这种谐波力矩实际上也较小，故略去不计.

1.4机构动力学

由于SADA固定安装在卫星本体上，SADA输出轴直接联结帆板旋转轴，从方程(3b)可以看出帆板驱动力矩即为其中的负载力矩TL.当考虑帆板挠性振动耦合和星体对驱动的耦合作用时，负载力矩可表述如下：

式中：Js为帆板绕旋转轴的转动惯量；Ω为星体角速度；q为帆板振动模态坐标；C1、C2为相应的耦合系数阵.

1.5模型简化

式(1)～(6)构成了SADA驱动模型，显然模型较复杂，为分析驱动机理得出合理结论，有必要对模型做合理地简化，主要有以下假设：

①通常电机互感系数较小，且两相步进电机通电电流相互正交，因此忽略电机绕组互感；

②随着电机制造工艺水平的提高，由其引起的电磁谐波力矩往往较小，因此忽略高次谐波力矩；

③简化模型中波动力矩只考虑步进电机不可避免的齿槽定位力矩，且只考虑占主要成分的4次谐波项；

④不计外界干扰力矩Td.

这样，可得到简化SADA模型如下：

Te=-ki1sin(Zrθ)+ki2cos(Zrθ)-

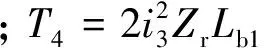
1.6模型验证

为验证模型合理性，对SADA做了不同转速、正反转情况下的仿真和实验测试研究.模型相关参数见表1，其中一些参数由厂商提供，部分参数则由经验值和相关测试数据拟合得到.电机采用正余弦256细分驱动，脉冲频率可根据指令转速求取.

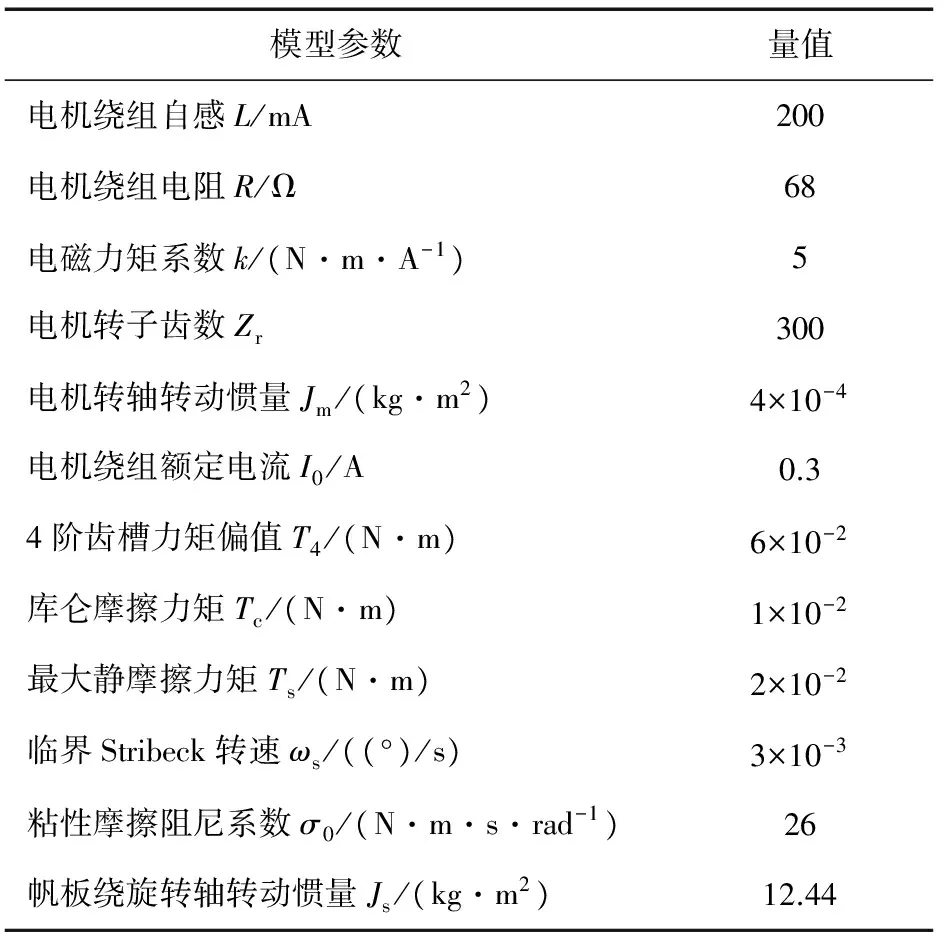
表1 SADA模型参数

测试帆板采用刚性梁代替，通过激光测振仪测量梁上某一测点速度，进而推导帆板转速并分析转速频率成分，并对帆板转速做了数值拟合，从而根据转矩平衡方程间接求得帆板驱动力矩.仿真是在Matlab环境下进行的，得出不同转速条件下的帆板转角、转速、转速频谱和驱动力矩.节省篇幅，这里只给出了0.06 (°)/s转速下的仿真和实验测试曲线图.图1为仿真结果，图2为测试曲线.表2汇总了各种转速下的转速主频率值和驱动力矩幅值.需要说明的是表2中驱动力矩幅值项，测试值是根据拟合测点振动速度进而推算的，仿真值可直接获得，图2显示力矩曲线波动较大，这里取峰值.

比较图1、图2和表2，可以发现仿真结果同实验测试结果基本吻合，从而也表明了模型的准确性.另外，通过仿真还能得出如下结论，这些结论有助于理解SADA驱动特性：

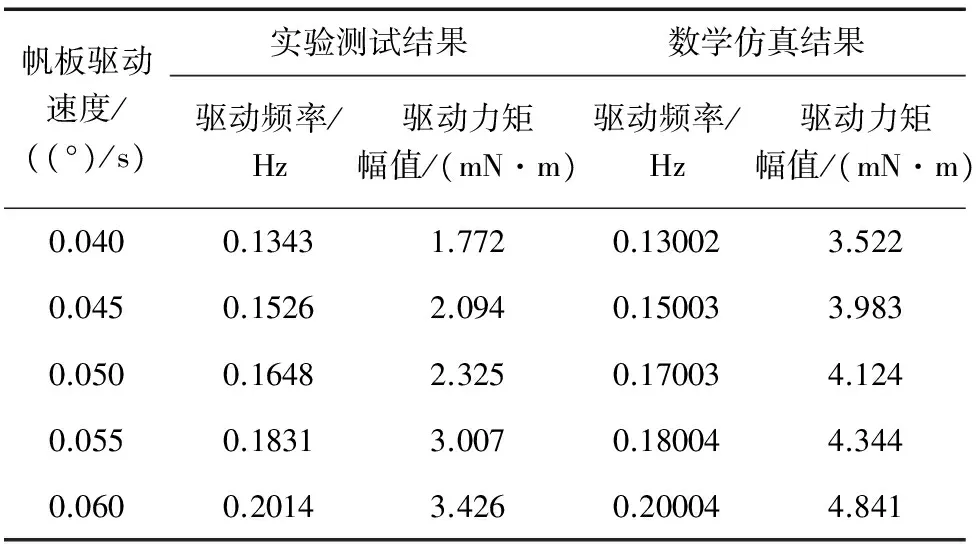
表2 数学仿真与实验测试结果

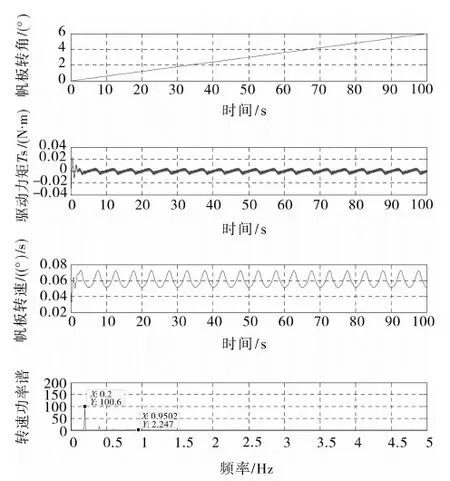
图1 0.06 (°)/s转速下的帆板转角、驱动力矩、帆板转速及频率分布图

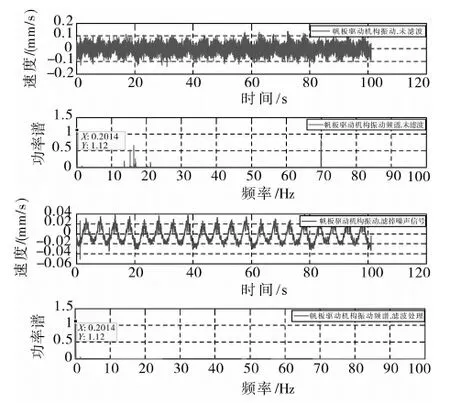
图2 0.060 (°)/s转速下测点的振动速度、频率分布图

①各种转速模式下，帆板基本能维持在该转速附近旋转；

②电机的每一次步进都会引起帆板转速较大波动，因为每一次步进电机都要经历一个加速—惯性—减速的过程；

③对两相步进电机而言，电机不可避免地会出现电磁旋转频率4n倍的谐振，特别是空载情况下，谐振频率特性更为明显；

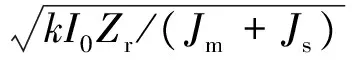
⑤电机的细分驱动在电机空载时对转速波动的改善效果更加明显，但当细分数大到一定时，电机驱动平稳度改善不太明显，以0.06 (°)/s转速为例，仿真显示128细分和256细分结果基本相同；

⑥机构中粘性摩擦系数对帆板转速波动幅值较大，因为步进的平稳性需要一定的阻尼为前提；

⑦电机4次谐波定位力矩幅值也影响着转速波动幅值，分析表明4次谐振频率为4f/K，也即电机步进频率.

2 SADA驱动控制初探

当前SADA驱动均为开环设计，SADA性能更多的是关注带动帆板跟踪太阳的能力.SADA作为卫星姿态重要干扰源之一，驱动平稳性也受到重视.这里只是探索两种理论上能改善SADA驱动平稳度的可行性方法，通常星体姿态和挠性振动(帆板不堵转前提下)对SADA驱动影响不大，这里所述的驱动控制均不考虑它.

2.1抑制波动力矩的电流补偿

这里的波动力矩是指方程(7d)中的电机齿槽定位力矩，从方程(7d)可以看出，当对绕组电流做补偿时，波动力矩对SADA驱动将不受影响.

通常电机电气时间常数远小于机械时间常数，为分析方便，这里忽略电机电流调节.假设在电机两相绕组正余弦电流基础上，再额外补偿幅值为I4、相位为α的电流，即令

此时，根据式(7d)可知电机力矩为

Te=kI0sin(2πn/K-Zrθ)+kI4sin(α-Zrθ)-

显然，当满足条件(10)时

补偿电流产生的力矩将完全抵消波动力矩，从而达到驱动平稳的目的.同理，该方法可推广到其他阶次谐波力矩的补偿.

图3比较了带电流补偿和不带电流补偿两种情况下的帆板转速波动曲线，从中可以看出，经补偿后的帆板转速更为平稳，但同时也看出，在帆板驱动开始阶段，由于摩擦作用，电机首先要克服摩擦力矩，因此转速不可避免存在较大波动.

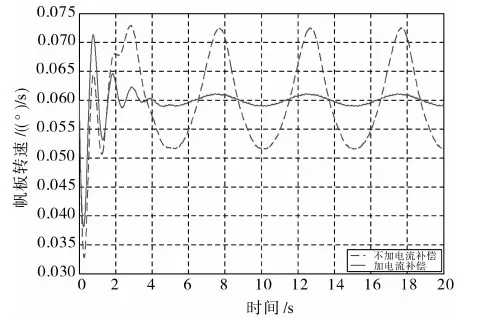
图3 电流补偿前后的帆板转速曲线

2.2自适应电流补偿

由2.1可知，当电机齿槽定位力矩占主要波动力矩时，采用这种补偿策略对改善帆板驱动平稳度效果明显，但这要求一定的模型准确性，而且摩擦作用还时刻存在.下面根据前述SADA模型，提出了一种自适应电流补偿方法，直接补偿摩擦力矩和波动力矩，该方法不需要准确的模型.

同上，这里不考虑电流调节过程.式(7d)所示力矩方程较为复杂，直接积分变换(DQ变换)是一种常用的反馈线性化方法[16].定义如下：

式中，id、iq分别为电机D轴电流、Q轴电流.

联立式(7d)～(7h)，得

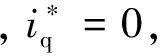
定义系统误差

e1θd-θ，e2

则有

式中：θd为期望转角；ωd为指令转速.

结合式(12)，可得

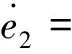
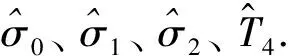
对式(12)描述的SADA驱动系统，构造如下非线性自适应控制律：

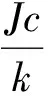
式中：c为设计的正常数.

相应参数估计值由下述自适应律确定

式中，kσ0、kσ1、kσ2、kT4为设计的正常数.

定理1.对式(12)描述的SADA驱动系统，在式(16)描述的自适应控制律和式(17)描述的参数更新律作用下，帆板驱动保持平稳.

证明.定义参数估计误差

预选Lyapunov函数

对其求导，可得

联立式(12)～(17)，略去中间推导过程，可得

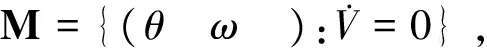
这样根据式(11)可求得电机绕组所需补偿电流

式中：D轴电流id=0，Q轴电流iq为式(16)所求.

需要说明的是上述电流补偿器需要用到电机转速，由于SADA中只有角位置传感器，角速度无法获取.但由于SADA电机采用细分驱动，控制脉冲频率实际上很高，而每一次脉冲对应的角位移都能测量，因此，可采用差分法并结合低通滤波器来近似估计转速.

图4比较了带自适应电流补偿和不带电流补偿两种情况下的帆板转速波动曲线，从中可以看出，经补偿后的帆板转速更为平稳，相比2.1节所述电流补偿，由于考虑了对摩擦的补偿，帆板驱动的开始阶段，转速平稳度也得到了明显的改善.

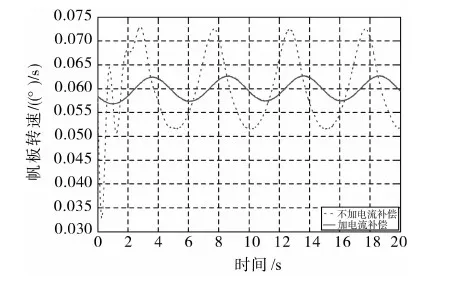
图4 自适应电流补偿前后的帆板转速曲线

3 结论

本文综述了国内外SADA建模研究进展情况，并在此基础上，以直接驱动型SADA为例，建立了较为完整的SADA模型.模型综合考虑了电机驱动、电机模型、机构传动以及负载特性，重点描述了SADA摩擦和波动力矩.通过数学仿真和实验测试验证了该模型的准确性和精确性.为提高帆板驱动平稳度，最后提出了两种电流补偿方法，数学仿真结果表明两种方法可大大改善帆板驱动平稳性.

由于国内SADA建模研究还不够系统深入，本文只是在SADA建模和SADA驱动方面做了初步探索，以望能从模型角度来解释一些帆板驱动特性，并能设计出相应的补偿方法以提升驱动平稳性，一些诸如工程实现等具体问题还有待深入研究.

[1] 高星, 王友平.太阳电池阵驱动机构的通用化、系列化和组合化设计[J].空间科学学报, 2002, 22(增刊2): 55-68

[2] Cabilic J, Fouriner J P.Design consideration on the solar array drive mechanism developed for SPOT[C].The 2ndSpace Tribology Workshop, ESTL, Risley, UK, 1980

[3] Altas G, Thomin G.Experiences of CNES and SEP on space mechanisms rotating at low speed[R].NASA, N87-29868, 1987

[4] Jones H M, Roger N.The design and development of a constant-speed solar array drive[R].NASA, N85-33519, 1985

[5] Rajagopal K R, Singh B, Singh B, et al.An improved high resolution hybrid stepper motor for solar array drive of Indian remote sensing satellite[J].IEEE Trans.on Industry Applications, 1997, 33(4): 906-913

[6] Etzler C C.Dynamic analysis of a bapta solar generator system[C].The 1stEuropean Symposium on Space Mechanisms and Tribology, Neuchatel, Switzerland, 1983

[7] Rodger F, Son N.Development of the solar array deployment and drive system for the XTE spacecraft[R].NASA, N95-27284, 1995

[8] Mario C R, Sebastiao E C V.Development of a BAPTA mechanism for small satellites[C].AAS Astrodynamics Specialist Conference, Girdwood, Alaska, 1999

[9] 王凤鸣, 刘暾, 张鹏顺.步进电动机驱动挠性负载时堵转机理研究[J].中国机械工程, 2002, 13(9): 771-773

[10] 秦文刚.步进电机驱动系统速度稳定度的研究[D].上海: 上海交通大学, 2006

[11] Aljaz K, Ales H, Karel J.Identification of stepping motor parameters[C].The International Conference on Computer as a Tool, Warsaw, 2007

[12] 黄晓海.太阳电池阵驱动机构摩擦力矩及干扰力矩的测试与分析[D].北京: 北京控制工程研究所, 1989

[13] Canudas C, Olsson H, Astrom K J, et al.A new model for control of systems with friction[J].IEEE Trans.on Automatic Control, 1995, 40(3): 419-425

[14] 莫会成.永磁交流伺服电动机转矩波动分析[J].微电机, 2007, 40(3): 1-4

[15] 钟宇明, 贾正春, 许强, 等.二相混合式步进电动机谐波转矩的仿真研究[J].微电机, 2004, 37(1): 13-15

[16] Bodson M, Chiasson J N, Novotnak R T, et al.High-performance nonlinear feedback control of a permanent magnet stepper motor [J].IEEE Trans.on Control Systems Technology, 1993, 1(1): 5-14

[17] Zhang W J, Fang Q H.Adaptive compensation for friction and force ripple in ship-borne gun servo system[C].The 7thWorld Congress on Intelligent Control and Automation, Chongqing, 2008

[18] Slotine J J E，Li W P.Applied nonlinear control[M].New Jersey: Prentice Hall, 1991

ResearchonModelingandDriverDesignofSolarArrayDriveAssembly

SI Zhuhua1,2，LIU Yiwu1,2，LI Kang1,2

(1.BeijingInstituteofControlEngineering,Beijing100190,China;2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190,China)

Domestic and overseas corresponding modeling research on solar array drive assembly(SADA) are summarized in this paper.Upon this work a quite systemic model is established, taking such issues as motor driver, motor model, mechanism and load characteristics into account with the emphasis on friction and motor ripple torque modeling.Simulation and experiment test results validate reality and accuracy of this model.In order to improve the solar array driving performance, two kinds of feasible current compensation methods are designed, and simulation results demonstrate that the two strategies can greatly improve the speed stability of solar array.

SADA; modeling; current compensation