自旋卫星测试转台精度分析

2010-12-11陶景桥孙小松

空间控制技术与应用 2010年2期

关键词：消旋加速度计模拟器

陶景桥，孙小松，李明

(北京控制工程研究所,北京 100190)

自旋卫星测试转台精度分析

陶景桥，孙小松，李明

(北京控制工程研究所,北京 100190)

自旋卫星测试转台用于自旋卫星控制系统的标定试验，是系统地面测试设备中的核心组成部分，其精度直接影响到系统标定试验的精度.另一方面，过高的转台精度指标将带来研制成本的大幅度增加，但有时仅对系统标定试验精度带来很小的提高，因此有必要对转台指标进行论证.根据标定试验原理，对转台引起的标定误差进行了分析计算，认为现有的精度指标能够满足标定需求，转台精度指标是合理的.

自旋卫星；测试转台；精度分析

转台标定测试是自旋卫星控制系统测试中的重要组成部分，转台是控制系统地面测试设备中的核心设备，因此转台性能的优劣直接影响测试数据的有效性.文献[1-4]对转台的精度进行分析，并给出了一些结论.本文针对自旋卫星测试转台，对由转台带来的标定误差进行逐项分析和计算，在忽略各项指标耦合作用情况下，将各项误差相加，得到最大可能的标定误差，以此来分析转台精度指标是否满足测试精度要求.

1 转台简介

本转台用于自旋卫星控制系统地面标定试验，包括：光学敏感器标定(太阳敏感器、红外地球敏感器)、惯性姿态敏感器标定(加速度计，用于卫星章动测量)、消旋系统标定.转台由两轴组成：内框轴又称自旋轴，可以连续旋转，具有速率控制功能，模拟卫星自旋运动；外框轴又称俯仰轴，具有角度位置控制功能，模拟卫星自旋轴姿态.转台机械结构示意图如图1所示.

转台主要精度指标如下：

自旋轴转速范围5～160 r/min；

自旋轴角速率测量精度±0.005 r/min；

自旋轴角速率控制精度±0.01 r/min，一周内的速率稳定度1×10-5；

自旋轴角位置测量精度±5"；

自旋轴角位置控制精度±15"；

俯仰轴角位置测量精度±5"；

俯仰轴角位置控制精度±15"；

两轴不交度0.07 mm；

两轴不垂直度10"；

自旋轴与台面不垂直度0.01 mm/Φ520 mm；

台面平面度7μm.

在实际使用中，各种工况下的转台使用情况如表1所示.

表1 转台使用情况

在考虑转台精度对系统标定精度的影响时，计算仅由转台引起的标定误差，并与被标定星上部件的精度指标进行比较.如果转台引起的标定误差小于被标定部件精度的十分之一，可以忽略转台误差的影响，认为可以满足系统标定试验精度要求.

2 太阳敏感器标定精度分析

2.1标定试验原理

太阳敏感器由直缝和斜缝组成测量自旋轴与太阳矢量夹角θs，测量几何关系如图2所示，计算公式见式(1)[5].

图2 太阳敏感器测量几何

标定试验时，将太阳模拟器光源光轴对准台面中心太阳敏感器方向，使太阳模拟器光轴与太阳敏感器中心处于同一水平位置.采用的方法是：通过台面中心设置45°平面镜，将太阳模拟器光轴基准引至转台俯仰轴Y轴方向的经纬仪，不断调整光轴方向直至满足要求,如图3所示.

图3 太阳敏感器标定原理

将太阳敏感器安装于台面中心，通过测量直缝和斜缝脉冲时间间隔，按照式(1)计算太阳角θs，以此来标定太阳敏感器的精度.

2.2转台精度分析

自旋轴速率精度对太阳敏感器标定的影响可忽略，因为标定时按照实际测得的转速来计算太阳角.

自旋轴速率稳定度为自旋一周内速率波动最大值与速率绝对值之比.假设V为最高标定转速110 r/min，一周内的稳定度1×10-5将在一周内引起的时间和角度差：

式(1)中的误差系数：

取极限情况，假设由自旋稳定度在ψss时间内引起的角度差为0.0036°，根据式(3)，按照太阳敏感器实际参数以及最大的标定角度30°，计算引起的太阳角标定误差为0.0035°(I=55°，ψ0=50°，ψss=73.8°，Δψss=0.0036°).

在实际标定中，通过测量直缝和斜缝脉冲中心的时间间隔Tss来计算式(1)中的ψss角度，

式中，Ts为实际测得的旋转周期.

连续取20个转速周期的数据进行平均，得到最后的标定结果.这样可以减小由转速不稳定引起的误差.

自旋轴测角误差5"将导致图3中太阳模拟器光轴在水平方向偏离理论方向10".当俯仰轴偏角为0°时，太阳模拟器光轴水平方向偏角对太阳角测量没有影响；俯仰轴转动角度α时，将导致太阳模拟器光轴与自旋轴夹角发生变化，如图4所示.根据球面三角o-A′BC[6]：

按照最大标定俯仰角度α=30°计算，由此引起的标定误差为：

可见，由自旋轴测角引起的误差可以忽略.

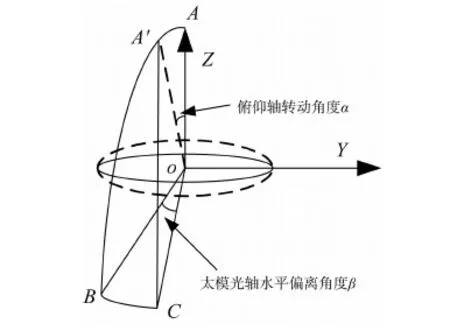
图4 太模光轴偏离示意图

俯仰轴位置测量精度将直接叠加到太阳角测角误差中，故引起的误差：5″≈0.0014°.

两轴不交度仅影响俯仰轴转动时太阳敏感器在太阳模拟器视场中的位置，可忽略.

两轴不垂直度影响分析见图5.不垂直度对0°俯仰轴偏角时的太阳角测量没有影响.当俯仰轴转角为β时，理论上自旋轴应该从A点沿oAB平面移动到A′点，但由于不垂直度α，实际上自旋轴从A点沿圆锥面oAA″移动到A″点，平面oA″C和平面oAC夹角即为真实俯仰轴转动角度β.根据球面三角o-AA″C：

按照最大标定俯仰角度β=30°计算：

根据球面三角o-ABA″，可以计算出太阳模拟器光轴和实际自旋轴方向的夹角∠A″oB.取最大的俯仰角度β=30°，不垂直度α=10″，则：

可见，由不垂直度引起的误差可以忽略.

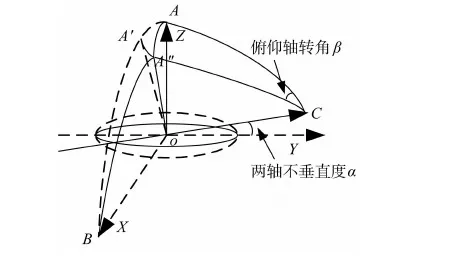
图5 两轴不垂直度分析

自旋轴与台面不垂直度将导致台面在不同的方向不能同时调平，自旋轴最大偏离角度：

根据以上分析，如果忽略转台各精度指标对太阳角影响的耦合作用，将各个精度指标单独作用引起的标定误差相加得到总的误差，如表2所示.

表2 转台引起的太阳角标定误差

太阳敏感器测角精度0.15°，由转台引起的标定误差为0.0060°，满足标定要求.

3 红外地球敏感器标定精度分析

3.1标定试验原理

红外地球敏感器为自旋扫描式红外地球敏感器，根据测得的地球弦宽，计算得到地心矢量与自旋轴之间的夹角[5].地面标定试验原理如图6所示，红外地球模拟器圆盘中心o点与转台台面中心地球敏感器中心o1点处于同一水平面，红外探头光轴通过转台自旋轴与俯仰轴交点，相对于台面有5°安装角.转台绕自旋轴Z轴旋转时，探头光轴扫过地模圆盘，得到半弦宽θ2(面o1oP与面o1BC的夹角)，通过计算可以就得到地心矢量角.

图6 地球敏感器标定原理

根据球面三角可计算得到：

3.2转台精度分析

根据式(11)计算误差系数如下，公式(11)中的θ1和θ2可以互换，故式(12)中θ1和θ2也可以互换

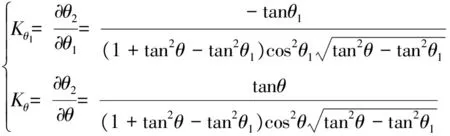
由于地球模拟器半张角θ=8.7°变化很小，可以不考虑公式中的θ常值变化，仅计算θ=8.7°时的误差系数.

自旋轴速率精度对地球敏感器标定没有影响，因为标定时按照实际测得的转速来计算地心角.自旋轴转速稳定度影响见式(2).在实际标定中，通过测量地中和地出脉冲的时间间隔Tes来计算式(11)中的θ2角度，如式(13).连续取20个转速周期的数据进行平均，得到最后的标定结果.

这样可以减小由转速不稳定引起的误差.取极限情况，根据式(2)，引起最大的旋宽误差为0.0036°.

自旋轴测角误差对红外标定没有影响.

俯仰轴位置测量精度将直接叠加到地心角误差中，引起地心角误差：5″≈0.0014°.根据误差分析式(12)，在转台俯仰轴3°位置(θ1=8°，Δθ1=0.0014°)附近可产生最大弦宽误差，误差约0.0033°.

两轴不交度0.07 mm将引起自旋轴与地模间的距离发生最大0.14 mm的变化，引起地模半张角θ发生0.0012°变化.根据误差分析式(12)，在转台俯仰轴3°位置(θ1=8°,Δθ=0.0012°)附近可产生最大弦宽误差约0.0031°.

两轴不垂直度的影响分析见式(7)，同理，对于地心角的测量，两轴不垂直度的影响可以忽略.

自旋轴与台面不垂直度分析见式(10)，同理，引起地心角测量误差为0.0011°，根据误差分析式(12)，在转台俯仰轴3°(θ1=8°)位置附近可产生最大弦宽误差约0.0026°.

综上分析，如果忽略转台各精度指标的耦合作用，将各个精度指标单独作用引起的标定误差相加得到总的标定误差，如表3所示.

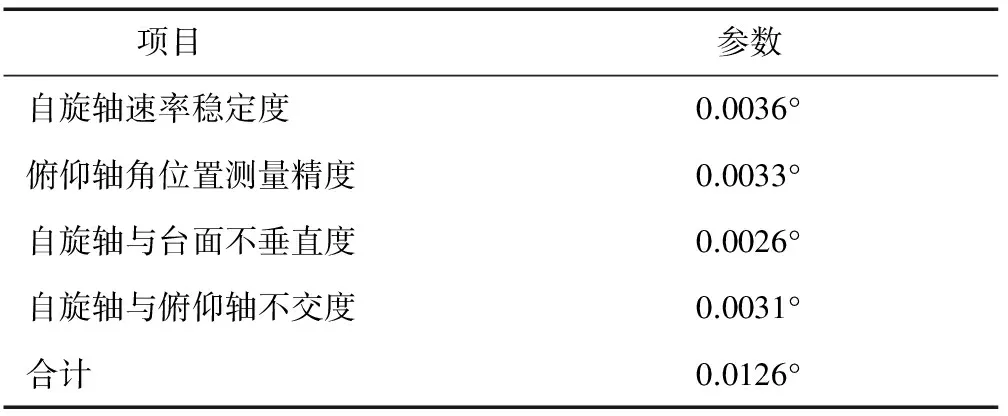
表3 转台引起的弦宽标定误差

地球敏感器弦宽精度0.15°，由转台引起的最大可能弦宽标定误差约为0.0126°，转台精度能够满足地球敏感器标定要求.

4 加速度计标定精度分析

4.1标定试验原理

加速度计在星上用于测量星体章动运动，其输入轴沿自旋轴安装.当星体有章动运动时，加速度计输入轴上有正弦规律变化的加速度输入信号，敏感出此正弦信号就能计算出星体的章动角[7].

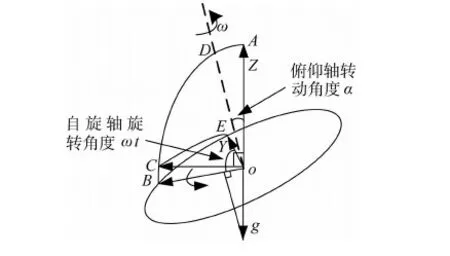
图7 加速度计转台标定原理

转台标定试验原理见图7.加速度计输入轴oB沿台面安装，当台面绕俯仰轴oE转过一定角度，自旋轴oD以一定角速度ω旋转，通过重力加速度g在加速度计输入轴oB上的分量，获得正弦变化的加速度物理激励输入信号.

根据球面三角o-BCE可得：

重力加速度g沿加速度计输入轴oB的分量为

另外，沿加速度计输入轴oB还有转台自旋运动的向心加速度常值分量，在章动控制中设置有带通滤波器，可以滤掉常值分量，故向心加速度可忽略.

实际标定中，根据加速度计的物理激励输入，测量加速度计输出信号、主动章动控制系统输出的章控脉冲时序，以检验整个章控系统是否满足要求.

4.2转台精度分析

自旋轴速率控制精度将影响加速度计输出正弦信号的周期.粗控脉冲由开关阈值产生；对于精控脉冲，在正弦信号负半周由相位钟测量信号周期，在正弦信号正半周开关阈值中间产生符合要求的精控双脉冲.由此可见，信号周期的细微变化仅对测试工况有细微影响，可以忽略，对章控脉冲的产生没有影响.

自旋速率稳定性影响正弦信号波形.根据式(2)，在最高测试转速30 r/min下周期误差约0.02ms，对波形的影响可以忽略.

自旋轴位置测量误差和控制误差对加速度计标定没有影响.

俯仰轴角位置测量精度将影响自旋轴的方向，进而影响到加速度计物理激励输入的正弦信号的幅值.俯仰轴角位置测量精度：5″≈0.0014°，由式(15)可知，将引起加速度计正弦输入信号幅值的变化约2.4×10-5g.

两轴不交度对台面旋转角度没有影响，故对加速度计标定没有影响.

两轴不垂直度将引起自旋轴方向发生变化，影响分析见式(7)和图5，在俯仰轴转动30°情况下，引起自旋轴方向发生的变化为3.9×10-8(°)，对加速度计标定的影响可以忽略.

自旋轴与台面不垂直度分析见式(10)，引起自旋轴方向发生最大变化0.0011°，由以上分析可知，引起加速度信号幅值误差约1.9×10-5g.

表4 转台引起的信号幅值误差

综合以上分析，转台精度对加速度计标定的影响表现在引起正弦输入信号幅值的变化，经计算将引起信号幅值变化约4.3×10-5g，与加速度计的阈值1×10-5g相当，其影响可以忽略.

5 消旋系统标定精度分析

5.1标定试验原理

消旋控制系统以红外地中脉冲为基准，使消旋位置磁头脉冲跟踪地中脉冲，相位差趋于零.

消旋系统标定时，将消旋组件、红外地球敏感器安装于转台台面上，消旋组件中心轴与转台自旋轴重合，红外地球敏感器按星上状态±5°安装角安装，并调整好地球模拟器.通过经纬仪，使消旋组件磁头中心、红外地球敏感器探头中心、地球模拟器中心处于转台自旋轴同一子午面内.当转台以额定转速旋转时，消旋转子平台以相同转速反向旋转，使消旋磁头脉冲与红外地中脉冲相位差趋于零，转子平台恒定指向地球模拟器中心.标定试验中，通过测量转子平台指向误差来标定消旋系统精度指标.

5.2转台精度分析

转台自旋轴速率精度影响地中信号周期.由于消旋系统以红外地中脉冲为基准信号，地中信号频率代表实际转速，故自旋轴速率测量精度和控制精度对消旋系统指向误差标定结果没有影响.但过大的速率误差会影响标定工况，现有的速率精度的影响认为可以忽略.

自旋轴速率稳定度分析见式(2)，在100r/min给消旋系统带来0.0036°的指向误差.同时，速率变化会导致系统指向不稳定，严重的将导致失锁.消旋系统指向精度指标为0.15°，即使0.0036°的角度突变也不会导致系统失锁.

自旋轴角位置测量精度和控制精度对消旋标定没有影响.

由于消旋系统标定都是0°俯仰角工况，故俯仰轴角位置测量精度和控制精度、两轴不交度等指标对标定没有影响.

由于消旋系统标定都是0°俯仰角工况，两轴不交度对标定试验没有影响，但消旋组件自旋轴和转台自旋轴的同轴度对标定有影响，将引起一定的指向误差.标定细则中规定，通过测量并控制消旋转子平台的端跳和径跳来消除不同轴度，同时也消除了自旋轴与台面不垂直度的影响.

综合以上分析，转台精度满足消旋标定要求.

6 结论

转台精度指标在现有标定工况下，对被标定星上部件引起的标定误差均小于其精度的十分之一，可以满足现有任务需求.同时，通过与转台研制单位的协商和沟通，认为转台精度属于中等精度，以现有的设计和制造水平可以达到，并且研制成本可以控制在较合理的范围内.故转台的指标是合理的.

从以上分析还可以看出，合理的地面标定方法可以减小转台带来的标定误差，从而降低对转台的要求.例如：太阳敏感器和地球敏感器标定中，通过取20个转速周期的数据进行平均，从而减小了自旋轴转速稳定度带来的误差；消旋标定时，测量并控制消旋转子平台的端跳和径跳，以此来减小转台两轴不交度带来的误差.

通过对转台指标的逐项分析，也可以看出各指标的重要程度.例如：对于各项测试，俯仰轴角度位置精度将带来较大标定误差，而自旋轴位置控制精度则主要是为了操作方便，不会带来标定误差；对于消旋标定，转速稳定度很重要.这样可以分辨出关键指标，在转台研制过程中对关键指标进行严格控制.

[1] 邵长胜，张广莹.高精度陀螺漂移伺服转台伺服精度的实验研究[J].中国惯性技术学报，2000(3)：73-78

[2] 曾宪菁，黄田，曾子平.3-RRR型数控回转台的精度分析[J].机械工程学报，2001(11)：42-45

[3] 王玉明，周兴义.测试转台轴线不正交对测量精度影响的分析[J].光学仪器，2008(2)：11-14

[4] 张锦江，陈兴林，李季苏.仿真转台机械回转精度对测量精度的影响分析[J].中国惯性技术学报，2000(6)：65-67

[5] 章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社, 1998:185-202

[6] 沈永欢，梁在中，许履瑚，蔡蒨蒨.实用数学手册[M].北京：科学出版社, 1992: 53-57

[7] 屠善澄.卫星姿态动力学与控制[M].北京：宇航出版社，2001：309-315

AccuracyAnalysisforSpinSatelliteTestTurn-Table

TAO Jingqiao, SUN Xiaosong, LI Ming

(BeijingInstituteofControlEngineering,Beijing100190,China)

A turn-table is used for spin satellite calibration test, and it is a key test equipment in spin satellite control system calibration test because its accuracy can influence the test accuracy directly.On the other hand,too high turn-table accuracy will cause high cost, but improve a little calibration accuracy, so it is necessary to analyze its parameters.Based on test principle, the test error caused by the turn-table error is analyzed, and it is concluded that the turn-table accuracy can meet the test need, and the turn-table accuracy parameters are reasonable.

spin satellite; test turn-table; accuracy analysis