一类平流层飞艇质量和惯量特性的计算方法与分析*

吴 雷，李 勇，李智斌

(1. 北京控制工程研究所，北京 100190；2. 空间智能控制技术重点实验室，北京 100190；3. 中国空间技术研究院，北京 100094)

一类平流层飞艇质量和惯量特性的计算方法与分析*

吴 雷1,2，李 勇3，李智斌1,2

(1. 北京控制工程研究所，北京 100190；2. 空间智能控制技术重点实验室，北京 100190；3. 中国空间技术研究院，北京 100094)

针对一类具有双拼椭球体外形的平流层飞艇，根据适当假设，给出该类飞艇质量和惯量特性的解析计算方法.以飞艇上升过程为例，通过仿真计算给出该过程飞艇质量、质心位置和转动惯量的变化曲线，结合理论分析，验证该计算方法的合理性.最后，简要分析了质量和惯量特性变化对飞艇运动稳定性和能控性的影响.

平流层飞艇；双拼椭球体；质量和惯量

平流层飞艇是一种依靠浮力升空、驻空的新型近空间飞行器. 作为一种新型应用平台，由于它在高性能通信、高分辨率对地观测和导弹预警等领域的巨大潜力，世界各大空间技术强国均投入大量经费对其进行论证和研发，并取得了很大的进展.

作为平流层飞艇研究的关键技术，飞艇的动力学建模方法一直是研究的重点. 目前关于飞艇建模的方法主要是仿照传统飞行器(飞机)的建模方法，再考虑其坐标原点与质心不重合和附加质量等特点进行改进[1-3]. 与之相关的主要研究领域集中在飞艇某特定飞行模式(不考虑质量变化)和将飞艇当作质点的研究上，这样就可以回避飞艇质量和惯量的局部变化给飞艇位置和姿态控制方法研究带来的困难.但作为平流层飞艇，其主要特点是通过吸、排空气来进行飞艇的高度和艇内外压差控制，尤其在飞艇的放飞和返回过程，飞艇的质量发生十余倍的变化，相应飞艇质量、惯量特性的研究就具有十分重要的意义.本文以目前广受关注的美国高空飞艇(HAA，high altitude airship)为对象，通过适当的假设，给出了此类飞艇质心位置、转动惯量的计算方法，并简要分析了质量和惯量变化对飞艇运动稳定性和能控性的影响.

1 飞艇参数

HAA的外形是由两个具有相同短半轴的半椭球体拼接而成的双拼椭球体，如图1所示，其相应参数引自文献[2]，大气环境参数引自文献[4].

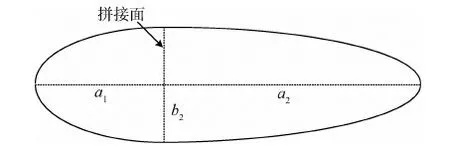
图1 HAA外形示意图

飞艇各参数如下：

长度L=250m；a1=L/3；a2=2a1；最大直径D=75m；b2=D/2；体积V=736311m3；蒙皮质量mf=24027kg；载荷质量mp=1814kg；结构和机构质量ms=19351kg；总的固定质量mt=mf+mp+ms=45192kg；飞艇内部氦气质量mhe=7938.1kg.据此可计算出飞艇在海平面高度时，其内部空气质量mair=848850kg；空气体积Vair=689610m3，约占飞艇总体积94%.

通过简单计算，在海平面和压力高度时飞艇内外气体压差分别为488Pa、369Pa.压差在合理范围内[5]，可见此组参数是合理的.

2 飞艇质心位置的计算

飞艇是由多部分质量组合而成的质点系，其质心位置的计算依赖于各部分的质心位置.固定质量mt的质心位置一般可以认为是固定不变的.但艇内氦气和空气的质心位置与其体积和分布情况密切相关，所以计算之前需要进行一些假设和坐标系定义.假设条件如下：

1)氦气和空气囊分界面为一半双拼椭球面，与飞艇具有相同的长半轴和一条相同的短半轴b1，另一条短半轴为b2，如图2所示.

2)固定质量当作质点考虑，忽略其体积.

3)艇内氦气和空气认为是均匀质量，且它们的温度和压力相同，不考虑氦气泄露，空气质量可变.

4)不考虑飞艇的形变.

5)飞艇能够稳定在水平姿态.

坐标系定义如下：

拼接面坐标系XYZo：原点在拼接面圆心，各轴与体坐标系平行.

图2 艇内气囊分布示意图

2.1艇内气体的质心位置

如图2所示，将飞艇内部气体体积划分为V1、V2、V3这3部分，其中V2、V3分别为2个半双拼椭球体，V1可以表示为一个半双拼椭球减去一个内切双拼椭球体.每一部分需要先分别计算2个四分之一椭球体的质心位置，再求出该部分的质心位置.所以先考察如图3所示均匀质量的四分之一椭球体的质心计算. 图中a、b、c为椭球体的各半轴长度，y为截面横坐标.

图3 四分之一椭球体

显然，质心在YOZ平面内.设其质心坐标为[0ygzg]T.

质心在Y轴上的坐标计算方法如下：

在y处截面的椭圆方程为

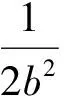
可得到该四分之一椭球体的质心在Y轴上坐标

用相同的方法计算出各部分气体质心在拼接面坐标系下的坐标，再转换到体坐标系下，最终获得内部气体的质心坐标为

其中：

zg1、zg2、zg3表示V1、V2、V3的质心坐标；V2=Vair-V/2.

2.2固定质量的质心位置

蒙皮质量可以看做一个薄壁空心双拼椭球，显然其质心在形心处.

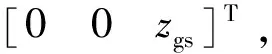
2.3飞艇的质心位置

将艇内气体和固定质量两部分结合起来，得到飞艇质心在体坐标系下坐标为

其中：

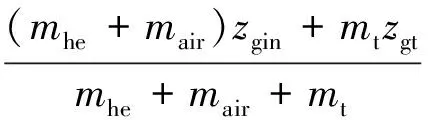
至此得到飞艇质心的计算表达式.但应注意到，上述方法是V2部分在飞艇XOY平面上方时的情况，当V2在下方时，只需进行相应的转换即可，这里不再赘述.

3 飞艇转动惯量的计算

3.1艇内气体转动惯量

由图2所示，艇内气体可划分为3个部分，每部分通过相应的四分之一椭球体组合得到.由文献[6]可知椭球体的转动惯量的计算方法.为了计算方便，可以先计算出各四分之一椭球体在拼接面坐标系的转动惯量，通过转动惯量的叠加原理求得艇内气体在拼接面坐标系下的转动惯量，再由平行轴定理计算出在体坐标系下的转动惯量.

V1部分的惯量可以由上半双拼椭球惯量减去V2部分半双拼椭球惯量得到，当V2在XOY平面之下时，则V3部分的惯量同上法得出.

因此可以计算出V1、V2、V3部分在拼接面坐标系的转动惯量：

至此得到艇内气体在拼接面坐标系的转动惯量

令Jc、Jg分别表示艇内气体在体坐标系和气体质心坐标系下的转动惯量，mg表示艇内气体质量，由平行轴定理[6]可知：

可以得到艇内气体在体坐标系下的惯量阵：

3.2固定质量的转动惯量

蒙皮质量的转动惯量可以当作薄壁空心双拼椭球来计算，方法与上面类似.由于蒙皮质量的质心在体坐标系原点，因此只需用一次平行轴定理即可求得其在体坐标系下的转动惯量阵Jf.集中质量当作质点，容易得到其转动惯量阵Js.

3.3飞艇的转动惯量

飞艇在体坐标系下的惯量阵为

由于飞艇具有纵对称面，则J具有如下形式：

其中，对角线元素为绕体坐标系X、Y、Z轴的转动惯量，Jxz为惯量积.

4 数值仿真与分析

为了验证上述计算方法的合理性，以飞艇的上升过程为例进行仿真.只考虑通过排放空气来调节自重使得飞艇能够平稳上升至压力高度，不考虑风场环境和其他的控制手段.假设飞艇保持平稳姿态以1m/s的垂直速度上升，不失一般性，可假设结构质量ms质心在30m处，则飞艇质量、质心和转动惯量的变化曲线如图4～7所示.

从仿真结果可以看出，在整个上升过程飞艇质量和惯量均发生很大的变化.结合文献[7]可以知道：质心的变化会改变相应执行机构的效力；质量和惯量的变化会影响动力学相应参数的改变；惯量积的变化会直接影响飞艇模型耦合的程度，最终会影响到飞艇稳定性和能控性.

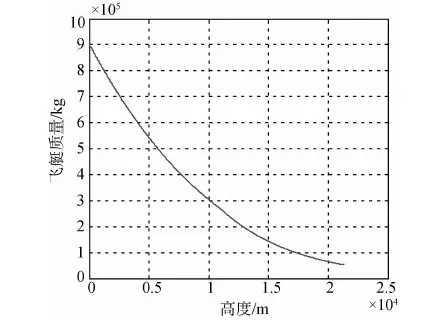
图4 飞艇质量变化曲线

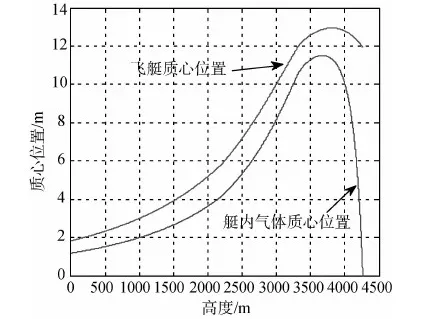
图5 飞艇质心位置变化曲线

图6 转动惯量变化曲线

图7 惯量积变化曲线

5 结束语

本文针对一类具有双拼椭球体外形的平流层飞艇的质量和惯量特性进行研究，通过适当假设，给出了此类飞艇质心位置和惯量阵的解析计算方法.仿真结果表明，飞艇受环境因素的影响非常巨大，尤其在上升和返回过程，质量和惯量的变化在一个数量级以上，质心位置也发生较大改变，集中体现了平流层飞艇变参数、大惯性、非线性和强耦合的特点.参数的变化会给相应的飞艇性能分析、控制器设计带来困难，在没有实际飞艇飞行数据可以参考的时候，通过本文给出的方法可以对此类飞艇放飞和返回过程中的质量和惯量进行估算.这样就可以建立变质量、变惯量的飞艇6自由度动力学模型，更加能够反映真实情况.在此基础上，可以对飞艇的全过程飞行进行稳定性、能控性分析和控制器的设计.

[1] Khoury G A，Gillett J D. Airship technology[M]. UK: Cambridge University Press,1999

[2] Mueller J B，Paluszek M A，Zhao Y Y. Development of an aerodynamic model and control law design for a high altitude airship[C]. AIAA The 3rd “Unmanned Unlimited” Technical Conference, Workshop and Exhibit, Chicago, September 20-23, 2004

[3] 陈澜，安锦文，杨常伟. 平流层飞艇建模关键问题研究[J]. 西北工业大学学报, 2007，5(3)：383-387

[4] 北半球标准大气[S]. 国防科学技术工业委员会，GJB 365. 1-87,1987

[5] 郑威，李勇，姚伟，等. 平流层飞艇高度方向稳态运动建模与特性分析[J]. 系统仿真学报， 2008，20(24)：6830-6838

[6] 赵新闻，杨兵初，黄生祥. 椭球体转动惯量的计算[J]. 物理与工程，2007，17(2)：28-29

[7] 王晓亮，单雪雄. 飞艇稳定性和能控性分析[J]. 计算机仿真，2005，22(8)：40-43

CalculationandAnalysisforMassandInertiaCharacteristicsofaClassofStratosphericAirship

WU Lei1,2, LI Yong3, LI Zhibin1,2

(1.BeijingInstituteofControlEngineering,Beijing100190,China；2.ScienceandTechnologyonSpaceIntelligenceControlLaboratory,Beijing100190,China； 3.ChinaAcademyofSpaceTechnology,Beijing100094,China)

In this paper, an analytic calculation method for mass and inertia characteristics of a class of stratospheric airship with double semi-ellipsoid shape is proposed according to proper assumptions. Variation curves of airship’s mass, position of mass center and inertia are given by simulating airship’s rising process. The rationality of this method is demonstrated based on theoretical analysis. At last, the influence of the airship’s mass and inertia characteristics on its stability and controllability are briefly analyzed.

stratospheric airship； double semi-ellipsoid shape； mass and inertia

*国家自然科学基金(11072028)资助项目.

2010-09-30

吴雷(1978—)，男，黑龙江人，博士研究生，研究方向为平流层飞艇自主飞行控制 (e-mail: wulei0451@163.com).

V448

A

1674-1579(2010)06-0039-04