基于神经网络动态逆的动力伞飞行控制方案*

钱克昌，陈自力，李 建

(军械工程学院，石家庄 050003)

基于神经网络动态逆的动力伞飞行控制方案*

钱克昌，陈自力，李 建

(军械工程学院，石家庄 050003)

动力伞飞行控制系统为复杂的非线性系统，通过对神经网络逼近逆系统的原理分析，提出一种由静态神经网络和积分器组成的动态神经网络，设计了基于神经网络动态逆方法的飞行控制方案，进行了飞行仿真验证，结果表明该方法完全满足系统控制的稳定性和鲁棒性要求，并具有良好的抗干扰能力.

动力伞；飞行控制；神经网络; 动态逆

动力伞是在滑翔伞基础上发展起来的,它的飞行控制系统是一个复杂的多输入多输出非线性系统，系统的输入输出关系远比线性系统复杂.同时系统各响应不满足叠加原理，各变量之间还存在耦合关系，使输入与输出之间的关系更加复杂.目前，对动力伞的飞行控制无论是在控制理论上还是工程实践上，都是一个难题.本文利用神经网络的逼近原理，将其与逆系统线性化解耦方法相结合，提出一种基于神经网络动态逆的控制方法，实验证明该方法是一种有效的控制方法.

1 逆系统方法的概念

不失问题的一般性，考虑由n个状态方程和p个输出方程表示的多变量非线性系统：

式中：x=(x1,x2,…,xn)T表示系统的状态向量，u=(u1,u2,…,uq)T表示系统的输入向量；y=(y1,y2,…,yp)T表示系统的输出向量；t0和x0分别为系统的初始时间和初始状态；f(·)，h(·)为局部解析的多元向量非线性函数.

根据系统可逆定理，式(1)表示的非线性系统在(x0,u0)的邻域内如果存在向量相对阶[1]α=(α1,α2,…,αq)T，则可以证明该系统存在逆系统：

式中，v为逆系统的输入，u为逆系统的输出，z为逆系统的内部状态，Aj，Bj为Brunovsky标准型矩阵，φ(·)为多元向量非线性函数.

由式(2)可以看出逆系统的内部状态z是由输入v通过多次积分获得的，而逆系统的输入中含有原非线性系统的状态反馈量x.将式(2)表述的逆系统串联在原系统之前，所组成的复合系统的输入输出关系满足：

式中nej为向量本性阶.可以看出，逆系统串联原系统组成的复合系统的输入输出具有线性传递关系，这种复合系统称之为伪线性复合系统.利用成熟的线性系统的理论就能实现线性系统的诸如解耦、极点配置、鲁棒伺服跟踪等目标，这就是逆系统控制方法的基本原理.

2 动力伞的动力学模型

动力伞飞行控制系统是一个复杂的多输入多输出非线性系统，操纵方式单一，只能通过拉拽伞衣后缘，改变伞衣的气动外形以及调节发动机动力来实现动力伞的飞行控制.而且动力伞独特的软翼结构容易受到风速、风向等外部环境的影响.这些都是建立动力伞动力学模型必须考虑的因素.

2.1基本假设

在下列基本的假设条件下，推导和建立动力伞系统的6自由度动力学方程：

(1)翼伞结构是展向对称的，伞衣完全张满后具有固定的形状.

(2)伞衣与承载机构刚性连接为一个整体.

(3)动力伞所受阻力远大于升力，对其升力忽略不计；且伞衣的压力中心和质心重合.

(4)惯性坐标系假设为平面大地.

动力伞的附加质量采用Barrows提供的附加质量矩阵形式，附加质量Aa,O的计算式为[2]

2.2动力伞系统的动力学方程

动力伞系统总的动量和动力矩由两部分组成，分别由真实质量和附加质量引起，系统的运动动力学方程可以根据动量和动量矩定理得到.

真实质量相对于坐标原点O的动量Pr,O和动量矩Hr,O可以表示为

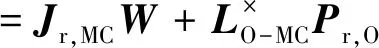
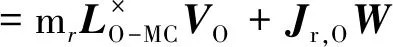
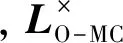
式(5)、(6)用矩阵形式表示为

根据附加质量表达式(4)，附加质量对应的动量Pa,O和动量矩Ha,O为

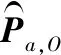
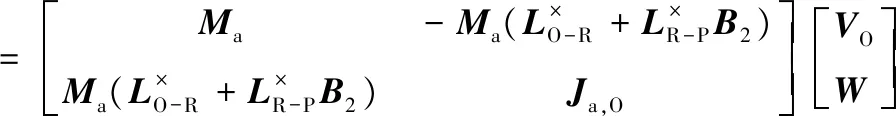
系统动量PT和动量矩HT用矩阵表示形式为式(7)和(8)之和，根据动量和动量矩定理，动力伞系统的动力学方程可以表示为[3]

3 神经网络动态逆控制

3.1实现动态逆的神经网络

动力伞飞行控制系统的逆系统是动态的，因此必须采用动态神经网络结构.采用动态神经元(如Hopfield动态神经元)构成的动态神经网络来逼近动态逆系统，在实际工程应用中还存在较多问题，一方面是其动态性能尚难把握，另一方面是这样构造的动态神经网络太复杂[4].

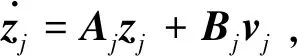
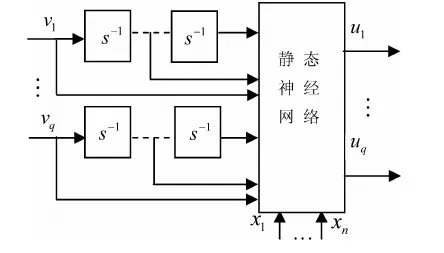
图1 神经网络结构

这种各司其职的结构能够克服由动态神经元构成的动态神经网络存在的问题，有助于简化神经网络的结构，便于工程实现.

3.2神经网络动态逆控制系统结构

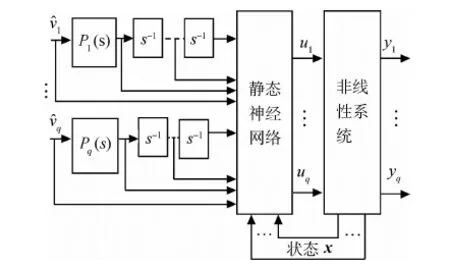
图2 神经网络动态逆控制系统基本结构

3.3神经网络的训练

控制系统采用反向传播BP神经网络，输入层有4个神经元，隐层有5个神经元，输出层有1个神经元，激励函数为

对神经网络采用直接离线训练和在线间接训练相结合的方式.离线训练时，直接将神经网络作为控制器串接在被控对象之前，训练算法选用Levenberg-Marquardt算法.训练时，首先产生一个限定最大幅值的、频率不定的方波序列，然后通过被控对象得到输出.

对神经网络直接离线训练，有可能得到错误的逆模型，特别是在系统的输入输出不是一一对应的情况下，因此，以在线的间接训练修正离线直接训练模型，间接训练算法采用Gauss-Newton方法，可以通过直接动态逆控制系统检验训练得到神经网络逆模型的精确度.

4 动力伞控制方案

4.1神经网络动态逆控制方案

在神经网络的输入层引入状态量M=[Φ,V,L](Φ为偏航角，V为水平速度，L为垂直速度)和状态变化量m=[φ,v,l](φ为偏航角速度，v为水平速度变化量，l为垂直速度变化量)，控制系统输出量为Q=[y1,y2,p](y1,y2分别为两边拉绳力度，p为发动机动力调节量)，控制方案框图如图3所示.

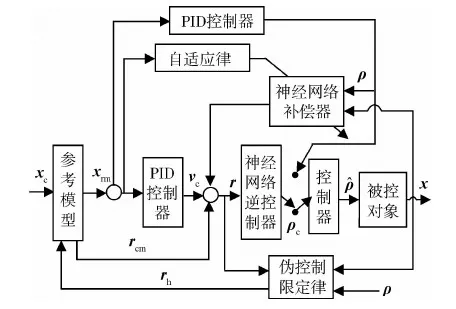
图3 控制方案框图

控制方案中参考模型为输出等于输入的直通模型.ρ为执行器的位置，针对动力伞飞行控制系统硬件能力限制的问题，引入伪控制限制方法(PCH)来补偿硬件上的不足，消除硬件特性的非线性干扰，伪控制信号为

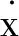
4.2仿真验证

基于式(9)利用Matlab建立6自由度动力伞非线性飞行仿真系统，为验证控制系统的抗干扰能力，引入含风模型[3].

仿真动力伞按照指定的速度和方向飞行.初始水平速度V=25m/s，初始偏航角Φ=0°，垂直速度L=0m/s.给定控制命令：偏航角Φ=10°，水平速度V=20m/s，垂直速度L=5m/s.仿真时间30s，仿真结果如图4所示.

图4 动力伞飞行控制仿真

在阵风干扰下，动力伞仍能按照指定控制命令稳定飞行，显示了神经网络动态逆控制方法良好的鲁棒性和抗干扰能力.

5 结 论

本文提出了基于神经网络动态逆方法的动力伞飞行控制方案，并完成了飞行仿真验证.仿真结果表明，设计的动态神经网络结构有良好的逼近非线性逆系统的性能，提出的控制方案能够顺利完成动力伞的飞行控制，对于阵风等环境因素的干扰具有很好的抗干扰性和鲁棒性.

[1] 戴先中.多变量非线性系统的神经网络逆控制方法[M].北京：科学出版社，2005

[2] Shin D H,Kim Y D.Reconfigurable flight control system design using adaptive neural networks[ J ].IEEE Transactions on Control Systems Technology,2004,12(1): 87-100

[3] 熊箐.翼伞系统动力学与归航方案研究[D].国防科技大学，2005

[4] Xu H J ,Mirmirani M,Ioannou P A.Robust neural adaptive control of a hypersonic aircraft[C ].AIAA Guidance,Navigation,and Control Conference and Exhibit,Austinm,Texas,Aug 11-14,2003

[5] Sun F C,Li H X,Li L.Robot discrete adaptive control based on dynamic-inversion using dynamical neural networks[ J ].Automatica,2002,38 (11): 1977-1983

FlightControlSchemeBasedonDynamicInversionofNeuralNetworkforPowerParafoil

QIAN Kechang,CHEN Zili,LI Jian

(OrdnanceEngineeringCollege,Shijiazhuang050003,China)

The flight control system of a power parafoil is a complicated nonlinear system.Based on the tracking principle of neural network,a dynamic neural network composed of a static neural network and integrators is presented.And then a flight control scheme based on the dynamic inversion for the power parafoil is designed.Simulation results demonstrate that the control method has strong ability of control and robustness.

power parafoil；flight control；neural network；dynamic inversion

*军队十一五装备预研基金(9140A25050106JB3412)资助项目.

2010-01-31

钱克昌(1984—)，男，江苏人，博士研究生，研究方向为无人机的智能控制理论和方法(e-mail:qiankechang@126.com).

V249；TP273

A

1674-1579(2010)04-0059-04