基于遗传算法的排课问题研究

吴 丰，万 径

（黄河水利职业技术学院，河南 开封 475004）

0 引言

2006 年，黄河水利职业技术学院（以下简称黄河水院）通过严格的评审程序，成为全国首批28 所国家示范性高等职业院校建设单位之一。 经过3 年的不懈努力，于2009 年通过了验收。 如今，学院已有两个校区、14 个系（部）、3 个教学部和1 个成人教育学院，在校全日制专科生15 000 余人。 在学院借助示范性建设这一机遇快速发展期间，教学管理的理念和模式也在悄然转变，其中教学信息化、管理科学化在提升学院管理水平方面发挥了不可替代的作用。

在进行教学工作之前的排课工作是教学管理的重中之重，课表编排的合适与否，关系到教学能否正常运行，是最基本的保障。 排课工作的信息化程度也能够从侧面反映出高校的办学实力、工作效率和教学质量。

1 黄河水院排课问题分析

1.1 排课问题是组合规划问题

课表指的是一张包含课程名、教师、上课地点和学时等信息的表，可以看做是这些信息的集合[1]。 课表编排则是严格依据教学计划，在确保教师、学生、地点三者时空不冲突的基础上，对所有要素进行组合规划，使得全校课表具有可实施性，并尽量满足人性化要求。

排课问题是一个多目标、有限资源、带有模糊约束条件的组合规划问题，而且是NP 完全的[2]。 多目标意味着能够解决课表问题的解有多种；有限资源是指高校可利用的教师、教室、时间资源；模糊约束条件指的是从明确的教学计划到明确的最终课表，而约束这一过程的条件却是模糊的。

1.2 约束条件

基本硬约束、硬约束和软约束是约束条件中的3 种类型[3]。

基本硬约束为：（1）在同一时间，同一学生不能上两门不同的课；（2）在同一时间，同一教师不能教两门不同的课程；（3）在同一时间，同一教室不能安排两门不同课程。

硬约束为：（1） 按照最小单位两节的形式上课；（2）实训课有自身的安排方式；（3）每门课程都有自己特定类型的教学资源；（4）教室必须足够大，能够容纳上课的学生；（5）某些课程可以先行手工排定时间和教室；（6）某些教师、班级或教室在某个时间段可能不能够利用。

软约束为：（1）课程表的课程尽量分布均匀；（2）教师尽量不连续上课，并在上课时间上存在一定的喜好；（3）一周有多个课次的同一课程，两次课之间应当有一定的时间间隔；（4）班级相邻，上课地点尽可能距离较近。

2 遗传算法设计

遗传算法具有自适应、 随机搜索和高度并行的特殊功能，使用遗传算法来近似求解排课这种带有约束的多目标优化组合问题，具有实际意义[4]。

2.1 基因编码

把一个三维立体的空间作为编码方案的出发点，将教师、教室、班级、时间和课程这5 个元素进行合理划分，通过三维空间中的坐标来进行编码。 假设这5 个元素为1 个5 元组，即：课程集合Subject=｛s1，s2，s3，…，sn｝；教师集合Teacher=｛t1，t2，t3，…，tn｝；班级集合Class=｛c1，c2，c3， …，cn｝； 时间集合Hour=｛h1，h2，h3，…，hn｝；教室集合Room=｛r1，r2，r3，…，rn｝。

在此5 元组中，由于课程、班级和教师已经在各系部录入教学计划任务的时候确定，所以将此3 元素捆绑在一起进行考虑，并叫做班级元组。 下面构造一个三维立体空间作为种群个体的模型，如图1所示。

亲子谈话是家庭中父母与子女间信息、观点、情感和态度的交流，以达到相互了解、信任与合作的过程(王争艳，刘红云，雷雳，张雷，2002)。同时，亲子谈话也是传递父母的信仰及信念的重要方式(Boyatzis et al., 2006)，实现家庭教育功能的途径之一(邓林园, 武永新, 孔荣, 方晓义, 2014; 房超, 方晓义, 2003)。因此，父母的来生信念可能会通过亲子谈话影响儿童对死亡和来世信念的理解，其中的关系及其作用机制仍值得进一步探讨。

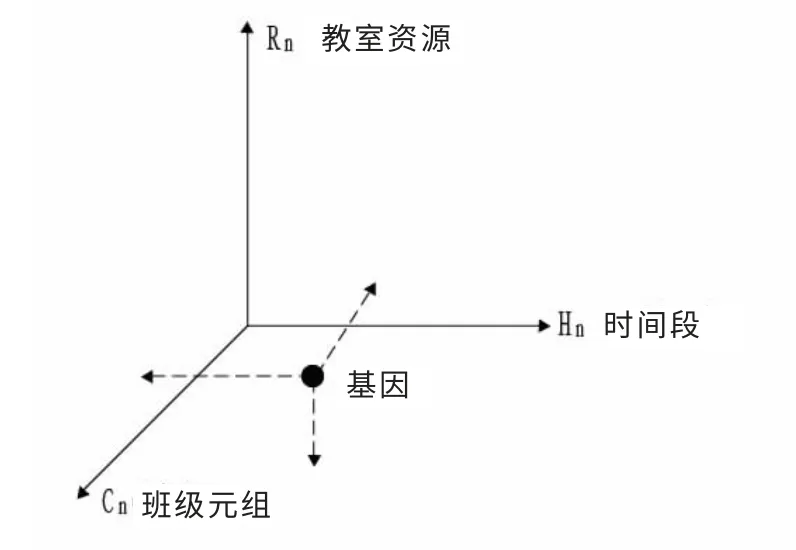
图1 三维立体个体模型Fig.1 Three-dimensional individual model

图中，H 坐标轴代表的是时间段，即从周一至周五，每2 小节为1 个时间段，1d 有4 个时间段，每周共计20 个时间段（H1~H20）。 R 坐标轴代表的是教室资源（R1~Rn，n 代表学校拥有教室的总数量）。 C 坐标轴代表的是班级元组。 这样，三维空间中的某个坐标就对应为某个班级的一门课程安排， 这里称为一个“基因”。 通过这种三维立体的个体模型将已知元素捆绑在一起考虑，此外只需要考虑时间要素和教室要素，减轻了编码的复杂程度。

2.2 基因编码

种群的生成是由计算机随机生成一个小于全校开课总任务数的随机整数， 然后从此整数开始，为每个开课任务分配上课的教室和上课时间，即可构成初始种群。 但是，这种随机生成种群的方法有可能引起种群个体在空间内分布不均，使得初始种群不能够代表整体种群的信息。 为解决这个问题，可以事先划分出多个子空间，在每个子空间中先各自产生自己的初始种群，然后再将这些初始种群汇总起来。 这样，构建的初始种群信息就相对均匀了一些，整体均匀性从而可以得到有效改善。

2.3 构造适应度函数

由于各个学校的实际情况不同，导致软约束条件不同，进而量化的方法也不尽相同。这里从3 个方面定义期望度值（课程离散度、黄金时段度、教师满意度），并将这3 个期望度值合理组合，构造适应度函数。

（1）课程离散度。 用全校所有班级大于“2 学时/周”的课程离散度期望值的平均值来衡量班级课程组合的优劣程度，即：

式中：di表示课程离散度期望值；n 代表全校所有班级大于“2 学时/周”的课程的总数。

（2）黄金时段度。 用全校黄金时段平均值来衡量每节课安排的优劣程度，即对所有开课计划的黄金时段期望值进行累加，再除以开课总数，即：

式中：hi代表课次的黄金时间期望值；n 代表总的开课数；为黄金时段度，其值越大，表明排课方案在周课表中的安排越好。

（3）教师满意度。 教师对课表的满意度用α1=1（满意）、α2=0.5（一般）和α3=0（不满意）表示，对应的满意与否的节数用β1、β2和β3表示。 这样，即可用公式（3）间接衡量教师的意愿，将θi累计再除以总体教师的个数，就是全体教师的满意度。

（4）适应度函数。 通过以上描述，适应度函数Fn可以构造为

这里λ1、λ2和λ3分别代表各期望值在总期望值中的权重。 该权重可以根据学院实际需求，由教务员自行设定。

2.4 设计选择遗传算子

这里采用轮盘赌选择法，其数学表达式为

式中：m 为群体大小；Fn为个体n 的适应度；Pn为遗传到下一代种群的概率。

具体做法是：为群体中所有个体都计算出适应度值，然后使用公式（5）计算每个个体被遗传到下一代种群中的概率，最后模拟轮盘赌操作，随机生成0至1 之间的随机数，与之前计算出的每个个体的概率进行匹配，确定某些个体是否被遗传到下一代种群中。

2.5 设计交叉遗传算子

这里采用的是单点交叉。 在进行交叉前，将众多排课方案按照“班级元组-时间-教室”的顺序排列下去，目的是将个体相互对应。 在交叉过程中，只需交叉对应班级元组的上课时间和所在教室即可。

2.6 设计变异遗传算子

个体变量的变异概率Pm不仅是产生新个体的辅助方法，而且还能对种群多样性起到保持作用，能够防止出现非成熟性的收敛。其值不能太大，如果取值大于0.5，遗传算法就变为随机搜索，从而使得遗传算法的数学特性和搜索功能不复存在。变异算法为：

（1） 在种群中随机选取个体的时间基因或教室基因。

（2）将此基因随机跳转为其他时间或教室。

（3）检测冲突。 如果检测到冲突，则再次跳转到其他时间或教室，并再次检测；如果没有发现冲突，则结束。

2.7 检测冲突

以三维立体空间编码方法为基础，将班级作为纵轴，将时间段作为横轴，再将课表的其他3 元素按“课程-教师-教室”的顺序排列，放置在由班级和时间段组成的二维坐标中。 通过这种二维坐标模型，只需根据硬约束条件对每个纵坐标中的课程、 教师和教室3 个元素进行检测，即可检测出冲突。

3 结语

通过实际的测试可以发现，适应度函数的值在较短的时间内收敛于“最优解”附近，其变化呈现出先剧烈后平缓趋势。 这充分验证了遗传算法中适应度函数的进化特征。总的来说，该算法在解决实际问题时取得了良好的效果，排课结果符合预期设计的目的。

[1] 腾姿,邓辉文,杨久俊. 基于遗传算法的排课系统的设计与实现[J]. 计算机应用,2007(27):199-201.

[2] 张海涛. 高等学校计算机排调课专家系统研究[D]. 阜新：辽宁工程技术大学，2005:48-49.

[3] 阎威. 排课系统中遗传算法的应用[J]. 内江科技,2008(3):3.

[4] 王小平,曹立明. 遗传算法：理论、应用与软件实现[M]. 西安交通大学出版社,2002:9.