基于改进粒子群算法的最优特征子集研究

侯大军，朱伟兴

(江苏大学电气信息工程学院，江苏镇江212003)

0 引言

特征选择是模式识别中的关键环节，特征选择质量的好坏直接影响到识别的成败，因此，受到科研人员的普遍重视。特征选择中的搜索问题是一个NP难题。穷尽式搜索由于其计算量过大，不可能得到广泛应用。1978年，Kittler J提出“分支定界算法”，它是一种自上而下方法，但具有回溯功能，可使所有的特征组合都被考虑到，这样计算量还是很大。此后出现的顺序前进法(SFS)，顺序后退法(SBS)以及改进的广义顺序前进法(GSFS)，广义顺序后退法(GSBS)等，这些启发式搜索策略实际上属于贪心类算法，搜索计算量较小，在原始特征之间相关性较小的情况下，这类算法能够取得较好的效果。但存在明显的缺点:特征一旦被加入或剔除，易出现搜索结果陷于局部最优的“筑巢”现象。为克服这些缺陷，出现了增1减r法(PTA)，先顺序加入1个特征再依次剔除r个特征，但这种l和r很难确定。Kudo M等人［1］提出了比启发式搜索更有优势的随机搜索策略，如遗传算法［2］，但出现早收敛、在进化后期搜索效率低的问题。鉴于以上情况 ，本文采用改进粒子群优化(PSO)算法提取出一组最优特征，进而验证了此方法的可行性。

1 特征选择建模与分类

在实际问题中，一般情况下在进行特征提取时会存在一些无关或不重要的特征，这些预先并不知道。无关或不重要的特征有可能引入噪声，甚至对识别的正确率有负面的影响。更进一步说，少量的特征可以减少系统的花费。因此，很有必要通过特征压缩来寻找一组最佳特征子集。图1为特征选择建模框架。

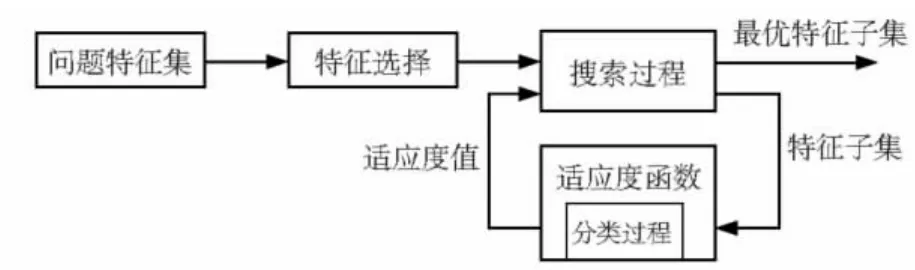
图1 特征选择建模框架Fig 1 Modeling of feature selection

1.1 改进的离散二进制PSO算法

1.1.1 离散二进制PSO算法基本原理与改进算法

基本PSO算法［3］是用于实值连续空间，然而，特征选择是组合优化问题，因而采用离散形式的PSO算法［3～5］。

根据下面2个公式来更新粒子的速度和位置为

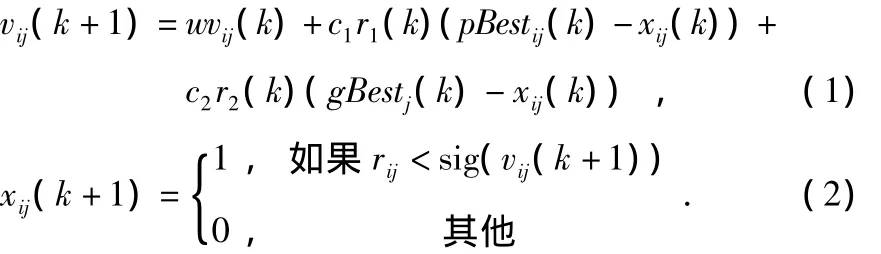
其中，vij(k)为粒子在第k次迭代中第j维的速度;r1，r2和 rij都是［0，1］之间的随机数，c1，c2都是学习因子;w 为加权系数;xij(k)为粒子i在k次迭代中第j维的当前位置;pBestij为粒子i在第j维的个体极值点的位置;gBestj为整个群在第j维的全局极值点的位置，而sig(vij(k))=1/(1+exp(－vij(k)))，为了防止sig(vij(k))函数饱和，将其修改为

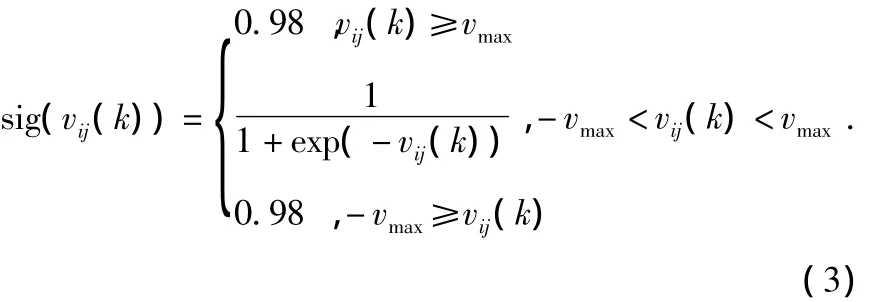
其中，vmax一般为［2，4］。

针对经典离散粒子群优化优化算法收敛性差和易陷入局部极值点的缺点，将式(1)改为粒子群a进化方程式(4)和粒子群b进化方程式(5)

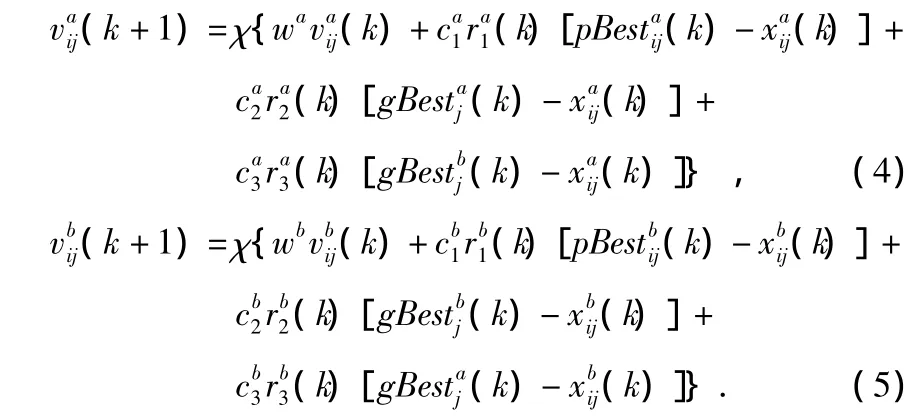
以上构造了2个独立的微粒群a，b，通过式(3)不必对这2个微粒群分别设置不同的速度上限，就可以使2个粒子群以不同的步长在搜索空间并行寻优。其中较大步长的粒子群全局搜索能力较强，可在搜索空间内进行快速寻优，而较小步长的粒子群则具有更好的局部寻优能力。

在群体智能算法计算中，为避免个体因早熟而降低寻优能力，必须在寻优过程中保证种群的多样性。为此，本文在两群微粒群算法的基础上，设计了一种新的变异算子，这种算子在进化前期不采取变异，当种群进化到一定的收敛时，则执行下面式子进行变异

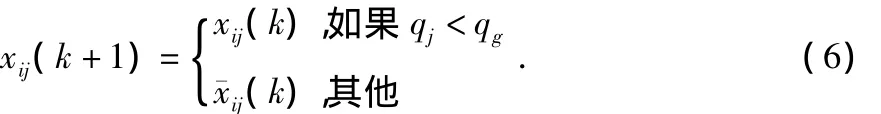
其中，qj表示微粒群中所有粒子的第j维的值(0或1)的个数与所有粒子的个数的比值，qg一般取0.7～0.9。

1.1.2 问题解的建立

假设在一个J维的目标搜索空间中，有m个微粒组成一个种群，其中，第i个微粒表示为一个J维的向量Xi=如果X的第j位为1，则此特征被选中;否则，没有被选中。

1.1.3 适应度函数［6］

粒子优劣性能评定标准定义如下

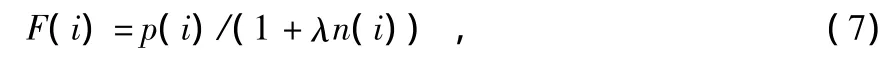
式中 F(i)为粒子i生成解的适应度值;p(i)为运用此特征子集进行分类的正确率的均值;n(i)表示此次选择的特征个数，即n(i)=xi1+xi2+…+xij;λ是特征个数的权重参数，一般取0.01。F越大，表明选择的特征子集表现越好，即利用较少的特征获得较高的分类正确率。

1.1.4 算法步骤

改进的PSO算法的流程:

1)初始化微粒群a，b(群体规模为m)，包括随机位置和速度;并比较最优位置;

2)根据式(2)，式(4)，式(5)调整微粒速度和位置;3)根据式(7)评价每个微粒的适应度;

4)在每个粒子群中，对每个微粒，将其适应值分别与其经过的最好位置pBbest和gBest作比较，如果较好，则将其作为当前的最好位置pBest和gBest;

5)判断群最优值是否优于前一次，如果是，直接跳至(6);否则，判断是否满足变异条件，如果否，则跳至(6)，若满足，则执行式(6)。

6)如果连续几代个体的平均适应度不变(其差小于某个具体的阈值)，就认为种群已成熟且不再有进化趋势，并以此作为算法终止的判定标准。进化结束后，选取末代种群中适应度最大的个体进行解码，就得到所要求的最优特征子集。否则，转(2)。

1.2 支持向量机识别分类

支持向量机(SVM)是20世纪90年代Vapnik基于统计学习理论提出的一种新的机器学习方法。本系统用改进后的PSO提取苹果的最优特征子集作为SVM的输入向量，对图像进行分类学习，应用LSSVM［7］分类器来验证特征选择的好坏。在这里选用径向基函数作为内核函数时可得到相对较好的分类效果。在采用LSSVM分类器识别的过程中，参数C和σ的取值对识别率有较大的影响。

2 实验结果

对于改进离散二进制PSO算法而言，通常取学习因子c1=c2=c3=2.05，w 取为0.7，种群 a 和种群 b大小都为30，设置最大迭代次数为100。实验样本共分4大类，每类60个样本(30个训练样本，30个测试样本)。在苹果识别系统中，根据苹果的形状和颜色特征［8，9］均将苹果分为特等品，一等品，二等品，等外品4个等级。

苹果形状特征包含:苹果横径，果形指数，周长，面积，占空比，等效圆半径，偏心率，形状参数，标准积，7个HU距。当惩罚因子C取20，径向基函数中的σ取1.3438时，形状识别的正确率最大。通过表1和表2分析实验结果，可以得到如下结论:

1)可以提取出最优特征子空间——苹果横径，果形指数，周长，面积，HU距1。并将原来16个3维特征压缩至5维，从而大大压缩了特征空间。同样，从平均识别率上看，所有原始特征的平均识别率为95%，而经特征选择后的平均识别率高达97.9%

2)离散二进制PSO算法的适应度一直小于改进后的离散二进制PSO，这是因为离散二进制PSO算法陷入局部极值点;同样从迭代次数上离散二进制PSO算法迭代了43次，根据文献［10］中的方法迭代了23次，而改进后的离散二进制PSO仅为17次，这样大大提高了算法收敛性。

3)在Celeron21.72 GHz，512 MB，Matlab7.6.0(R2008a)上，从算法的算法运行时间上看，离散二进制PSO算法为450 ms，文献［10］中的方法运行时间仅为270 ms;但改进后的离散二进制PSO算法为386 ms。

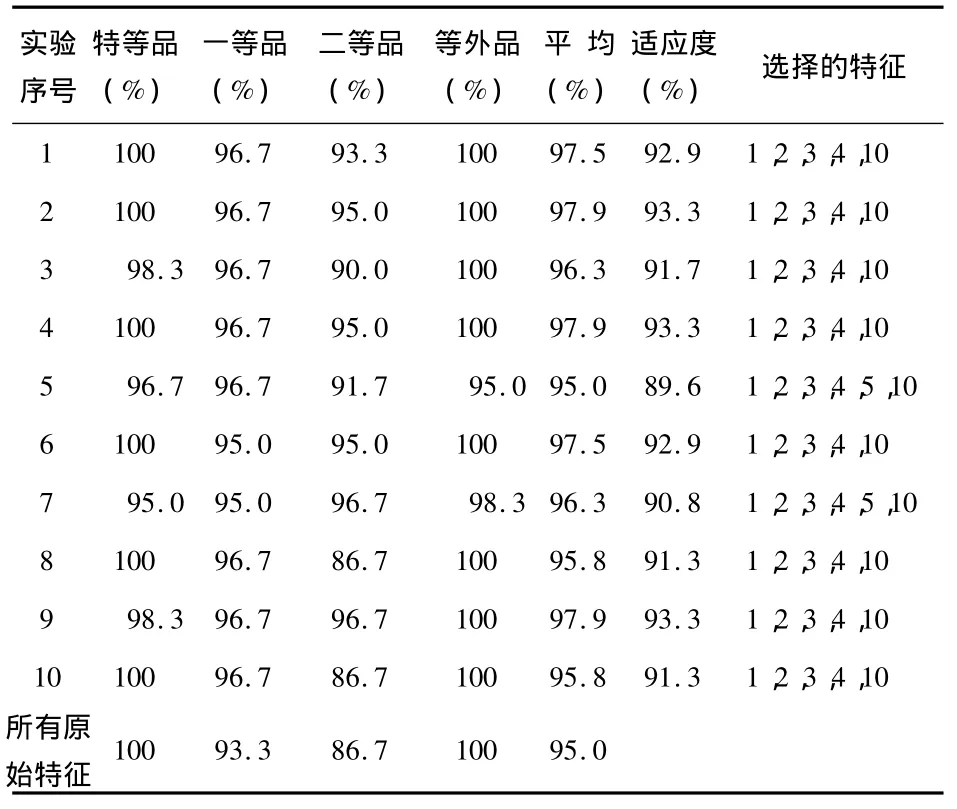
表1 改进的离散二进制PSO10次特征选择和分类结果Tab 1 10 times feature selection and classification results of modified binary PSO

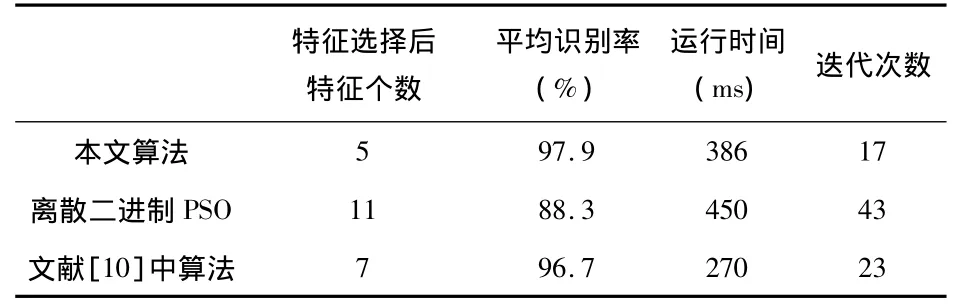
表2 3种算法比较Tab 2 Comparison of three algorithms

3 结论

本文提出了一种基于改进PSO算法的快速特征选择方法。该方法运用改进PSO算法从特征样本中提取一组最优特征子空间;之后利用LSSVM分类器来验证此方法的可行性。此算法虽然克服了算法收敛性慢和易引入陷入局部极值点的缺点，迭代次数比离散PSO和文献［10］中的方法要小，但也引入了新问题(如增加了算法的空间复杂度和当原始数据大于1000维以上需要调整适应度函数)，它们在后期的工作中有待解决。

［1］Kudo M，Sklansky J.Comparison of slgorithms that select features for pattern classifiers［J］.Pattern Recognition，2000，33(1):25－41.

［2］Lu Jianjiang，Zhao Tianzhong，Zhang Yafei.Feature selection based on genetic algorithm for image annotation［J］.Knowledge-based Systems，2008，21(8):887－891.

［3］Bergh Frans v d，Engelbrecht A P.A cooperative approach to particle swarm optimization［J］.IEEE Transactionson Evolutionary Computation，2004，8(3):225－239.

［4］Khanesar M A.A novel binary particle swarm optimization［C］∥The15th Mediterranean Conference on Control and Automation，2007.

［5］Kennedy J，Eberhart R C.A discrete binary version of the particle swarm algorithm［C］∥IEEE International Confererce on Systems，Man and Cybernetics，1997:4104－4108.

［6］Pan Li，Zheng Hong.Genetic feature selection for texture classification［J］.Geo-spatial Information Science，2004，7(3):162－166.

［7］Suykens J A K，Vandewalle J.Recurrent least squares support vector machines［J］.IEEE Transaction on Circuits and Systems-I，2000，47(7):1109－1114.

［8］Unay D，Gosselin B.Stem and calyx recognition on ＇Jonagold＇apples by pattern recognition［J］.Journal of Food Engineering，2007，78(2):597－605.

［9］Ji Haiyan，Yuan Jinli.The application study of apple color grading by particle swarm optimization neural networks［C］∥The 6th World Congress on Intelligent Control and Automation，2006:2651－2654.

［10］李勇明.内嵌多准则的遗传算法用于尿沉渣红白细胞的特征选择［J］.系统仿真学报，2008，20(14):3853－3863.